Презентація на тему:
Метод координат на площині

Презентація курсу за вибором “Метод координат на площині”

Метод координат на площині. Аналітична геометрія — розділ геометрії, що вивчає властивості геометричних фігур засобами елементарної алгебри (в ширшому розумінні — засобами математичного аналізу), пов'язуючи їх з застосуванням методу координат.

Основоположники аналітичної геометрії Основні положення аналітичної геометрії вперше сформулював філософ і математик Р. Декарт. Г. Лейбніц, Л. Ейлер, І. Ньютон надали аналітичній геометрії сучасної структури.

Декартові координати на площині. Прямокутна система координат на площині вважається заданою, якщо на площині вказано: а) дві взаємно перпендикулярні прямі, на кожній із яких вибрано додатній напрям - осі ординат (вісь абсцис і вісь ординат). Точка О перетину цих координат називається початком координат; б) одиничний відрізок; Прямокутними декартовими координатами довільної точки площини називається впорядкована пара чисел і , де - координата проекції точки на вісь абсцис, а - координата проекції точки на вісь ординат. Той факт, що точка має координати і , записується так: .

1.2 Відстань між двома точками Відстань між двома точками обчислюється за формулою: Приклад 1. Обчислити відстань між точками і Розв’язання:

1.3 Ділення відрізка в даному відношенні Координати точки , яка ділить відрізок у відношенні знаходяться по формулі: При діленні відрізка навпіл, тобто при , отримуємо такі формули:

Приклад 1. Відрізок, обмежений точками і поділено на три рівні частини. Знайти координати точок поділу і Розв’язання: Точка С ділить відрізок АВ у відношенні . Отже, Отже, .

Точка Д ділить відрізок АВ у відношенні Звідси Отже,

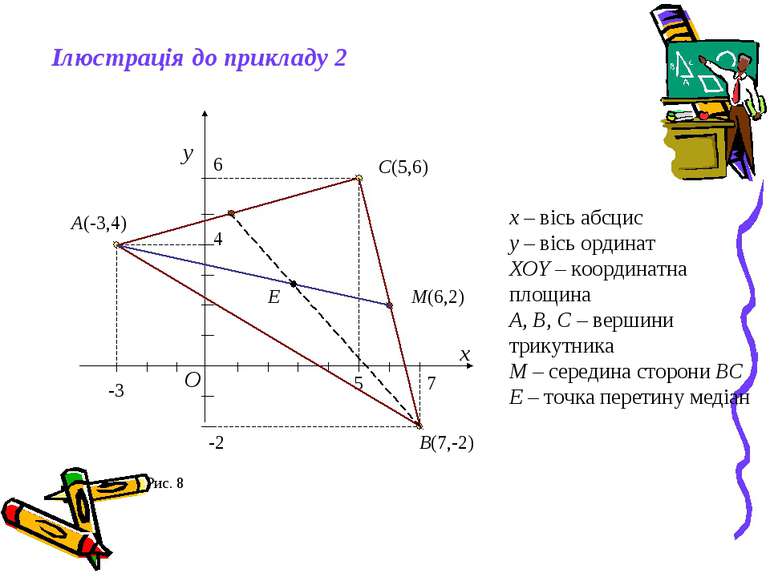
Приклад 2. Трикутник ABC задано координатами вершин A(–3;4), B(7; –2), C(5;6). Побудувати ∆ABC в системі координат. Знайти: а) довжину медіани AM; б) точку E перетину медіан. (рис. 1) Нехай M – середина сторони BC: За властивістю точки перетину медіан трикутника Тоді координати точки E:

-3 4 A(-3,4) 7 -2 B(7,-2) 5 6 C(5,6) M(6,2) E Ілюстрація до прикладу 2 x y O x – вісь абсцис y – вісь ординат XOY – координатна площина A, B, C – вершини трикутника M – середина сторони BC E – точка перетину медіан Рис. 8

Пряма на площині 1.4 Загальне рівняння прямої. 1.5 Кутовий коефіцієнт прямої. Рівняння прямої з кутовим коефіцієнтом. 1.6 Рівняння прямої, яка проходить через дану точку в заданому напрямі. 1.7 Рівняння прямої, що проходить через дві задані точки. 1.8. Рівняння прямої у відрізках на осях. 1.9 Перетин двох прямих.

1.4 Загальне рівняння прямої. Якщо на площині довільно взято декартову систему координат, то будь – яке рівняння першого степеня відносно координат і , де визначають пряму в цій системі координат.

Окремі випадки загального рівняння прямої Значення коефіцієнтів Рівняння прямої Розміщення прямої 1 С=0 Пряма проходить через початок координат. 2 А=0 Пряма паралельна осі абсцис. 3 Пряма паралельна осі ординат. 4 Пряма співпадає з віссю абсцис. 5 Пряма співпадає з віссю ординат.

1.5Рівняння прямої з кутовим коефіцієнтом Нехай похила пряма l утворює кут α з віссю Ox і перетинає вісь Oy у точці B(0;b) (рис. 10). Рис. 10 l x O α y x Нехай M(x; y) – довільна точка прямої l. У прямокутному ΔBNM MBN=α. Тоді y – b = kx . Звідси маємо рівняння прямої з кутовим коефіцієнтом y = kx + b. Зауваження 1. Якщо b=0, то пряма y=kx проходить через початок координат O(0;0). Якщо k=0, то пряма y=b паралельна осі Ox (горизонтальна). Зауваження 2. Якщо пряма паралельна осі Oy (α=90º), то її кутовий коефіцієнт не існує (k = tg 90º = ∞), і її рівняння не можна подати у відповідному вигляді. Рівняння вертикальної прямої має вигляд x=a, де a – абсциса точки перетину A(a;0) з віссю Ox. Тангенс кута нахилу α називають кутовим коефіцієнтом k прямої l: k=tgα. Число b називають початковою ординатою прямої l.

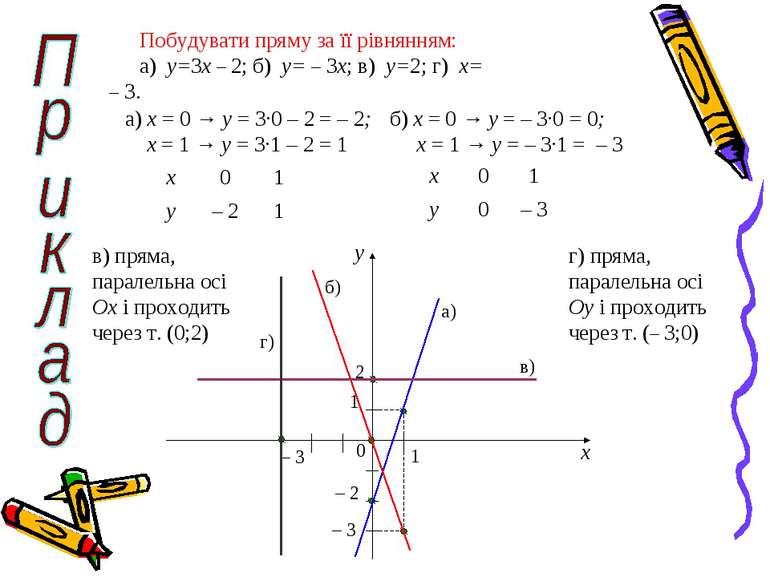
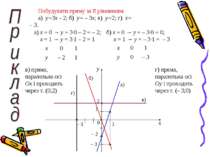
Побудувати пряму за її рівнянням: а) y=3x – 2; б) y= – 3x; в) y=2; г) x= – 3. в) пряма, паралельна осi Оx i проходить через т. (0;2) г) пряма, паралельна осi Оy i проходить через т. (– 3;0) а) x = 0 → y = 3·0 – 2 = – 2; x = 1 → y = 3·1 – 2 = 1 б) x = 0 → y = – 3·0 = 0; x = 1 → y = – 3·1 = – 3 x y 0 – 2 1 1 а) – 3 б) 2 в) – 3 г)

1.6 Рівняння прямої, яка проходить через дану точку в заданому напрямі. Рівняння прямої, яка проходить через дану точку в заданому напрямі, має вигляд , де - кутовий коефіцієнт прямої. Це рівняння можна розглядати як рівняння пучка прямих, тобто множини прямих, які проходять через ту саму точку площини - . Зазначимо, що тільки одна пряма з усіх прямих, що проходять через точку , а саме пряма, перпендикулярна до осі , не виражається цим рівнянням. Її рівняння має вигляд .

Написати рівняння і побудувати пряму, що належить пучку з центром у точці M1(–3,1), якщо: а) пряма паралельна осі Ox; б) пряма паралельна осі Oy; в) пряма нахилена до осі Ox під кутом α=60º. а) якщо пряма паралельна осi Оx, то k = 0: y – 1= 0, y = 1; б) якщо пряма паралельна осі Oy, то її рівняння має вигляд x = – 3; в) якщо пряма нахилена до осі Ox під кутом α=60º, то k = tg 60º = y – 1= (x+3); y = x+3 +1 y x а) б) 0 1 в) – 3 6,2 – 1 4,5 M1(–3,1) x 0 -1 y 6,2 4,5

1.7 Рівняння прямої, що проходить через дві задані точки. Рівняння прямої, що проходить через дві задані точки має вигляд . Кутовий коефіцієнт прямої, яка проходить через точки А і В, визначаємо з співвідношення .

Приклад 1. Складіть рівняння прямої, яка проходить через точки Розв’язання: За умовою Підставивши ці значення в рівняння , дістанемо .

За властивістю бісектриси внутрішнього кута трикутника Тоді Приклад 2. Трикутник ABC задано координатами вершин A(1;–2), B(–5;1), C(3;–1). Побудувати ∆ABC в системі координат (рис. 11). Знайти рівняння бісектриси AL. y x А(1;–2) В(–5;1) С(3;–1) L Рис. 11 O 1 –2 –5 1 3 –1

1.8 Рівняння прямої у відрізках на осях. Рівняння прямої у відрізках на осях має вигляд , де а і b - відповідно абсциса і ордината точок перетину прямої з осями і . Оx

Розв’язання: За умовою Отже, шукане рівняння має вигляд : . Приклад. Скласти рівняння прямої, яка перетинає вісь у точці , а вісь ординат у точці

Кут між прямими. Умови паралельності та перпендикулярності прямих Нехай прямі l1 і l2, що зображені на рис. 1, мають задані кутові коефіцієнти відповідно k1 і k2. Оскільки tgα1 = k1; tgα2 = k2, то тангенс кута між прямими знаходиться за формулою φ = α2 – α1; Рис. 1 α1 α2 O l1 l2 α2 φ α1 x y Для паралельних прямих φ = 0, tgφ = 0, а для перпендикулярних прямих φ = 90º, tgφ → ∞. З одержаної формули випливає, що 1) необхідною і достатньою умовою паралельності невертикальних прямих l1 і l2 є рівність k1 = k2; 2) необхідною і достатньою умовою перпендикулярності похилих прямих l1 і l2 є рівність k1k2 = – 1. Зауваження. Кут між прямими φ розуміється як кут повороту. Гострий кут між прямими знаходиться за формулою Тоді для кута φ між ними маємо

У тупокутному ΔABC ( – тупий) задано рівняння сторін AB: y = – 3x + 5, AC: y = 2x – 10 і координати вершини C(2; – 6). Знайти: а) ; б) рівняння висоти CN; в) рівняння середньої лінії ML, що паралельна AB, де M – середина сторони AC. (рис. 14) а) Знайдемо гострий кут між прямими AB і AC: Тодi б) в) M – середина сторони AC: kAB = – 3; kAC = 2; 32

Перетин двох прямих. Якщо дано дві прямі які перетинаються, то щоб визначити координати точки перетину цих прямих, треба розв’язати систему рівнянь даних прямих.

Приклад 2. Знайдіть вершини трикутника, якщо його сторони задано рівняннями , , , Розв’язання: Щоб знайти координати вершин трикутника, треба розв’язати три системи рівнянь: Розв’язок першої системи: Розв’язок другої системи: Розв’язок третьої системи: Отже, вершинами трикутника є точки:

Розділ 2. Лінії другого порядку 2.1 Загальне рівняння ліній другого порядку. 2.2 Коло. 2.3 Еліпс. 2.4 Гіпербола. 2.5 Парабола.

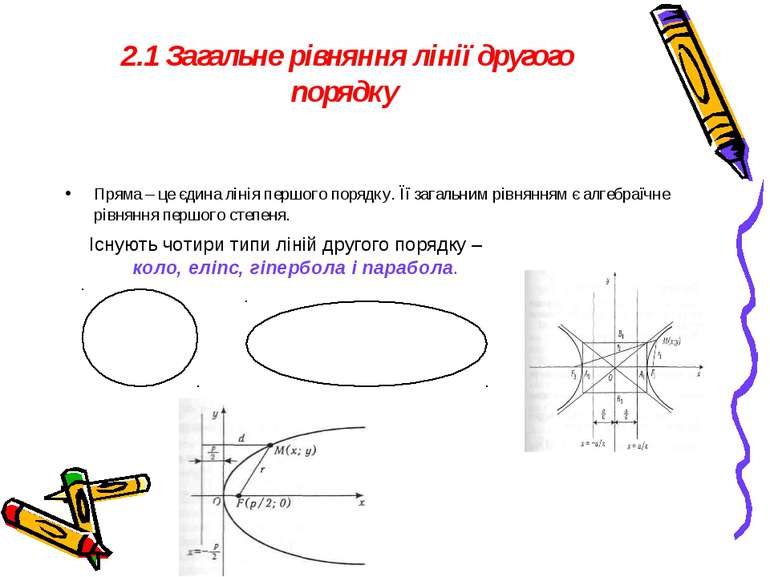
2.1 Загальне рівняння лінії другого порядку Пряма – це єдина лінія першого порядку. Її загальним рівнянням є алгебраїчне рівняння першого степеня. Існують чотири типи ліній другого порядку – коло, еліпс, гіпербола і парабола.

2.2 Коло Колом називається множина всіх точок площини, рівновіддалених від даної точки цієї площини, яку називають центром. Кола з центром у початку координат і радіусом має вигляд: . Рівняння кола з центром у точці і радіусом має вигляд: Рівняння кола в загальному вигляді записують так: , де - сталі коефіцієнти.

Переконатись, що рівняння 3x2 + 3y2 + 6x – 5y – 9 = 0 є рівнянням кола. Знайти його центр C(a;b) і радіус r. x2 + y2 + 2x – (5/3)y – 3 = 0; (x + 1)2 + (y – 5/6)2 = (13/6)2; C(– 1; 5/6); r = 13/6. Дано дві точки A(2; –3) і B(–6; 1). Скласти рівняння кола l, для якого відрізок AB служить діаметром. Центром кола l є середина C діаметра AB, а радіус кола r = AB/2. Тоді: Рівняння кола

Еліпсом називається множина точок площини, сума відстаней яких до двох даних точок, що називаються фокусами, є величина стала , більша за відстань між фокусами . 2.3 Еліпс

Рівняння еліпса: Залежність між параметрами , , , виражається співвідношенням: Точки перетину еліпса з осями координат , , називаються вершинами еліпса. Форма еліпса ( міра його стиску характеризується його ексцентриситетом , тобто Директрисами еліпса називаються дві прямі, паралельні малій осі , які віддалені від неї на відстань ( коло директрис не має). Рівняння директрис має вигляд : . де ; - довжина малої півосі.

Переконатись, що рівняння 9x2 + 100y2 – 900 = 0 є рівнянням еліпса. Зобразити ескіз еліпса, знайшовши точки його перетину з осями координат (вершини еліпса). еліпс, що перетинає осі координат у вершинах A1(– 10,0), A2(10,0), B1(0, –3), B2(0,3). x y A1 A2 B1 B2 O 3 – 3 –10 10

2.4 Гіпербола Гіперболою називають множину точок площини, абсолютна величина різниці відстаней яких до двох даних точок, що називаються фокусами, є величина стала , менша за відстань між фокусами .

Рівняння гіперболи: де Точки , називаються вершинами гіперболи, а точки , називаються уявними вершинами гіперболи. Відрізок називається дійсною віссю, а відрізок і його довжина - уявною віссю. і його довжина Ексцентриситетом гіперболи називається відношення відстані між фокусами до дійсної осі: Гіпербола має дві асимптоти, рівняння яких:

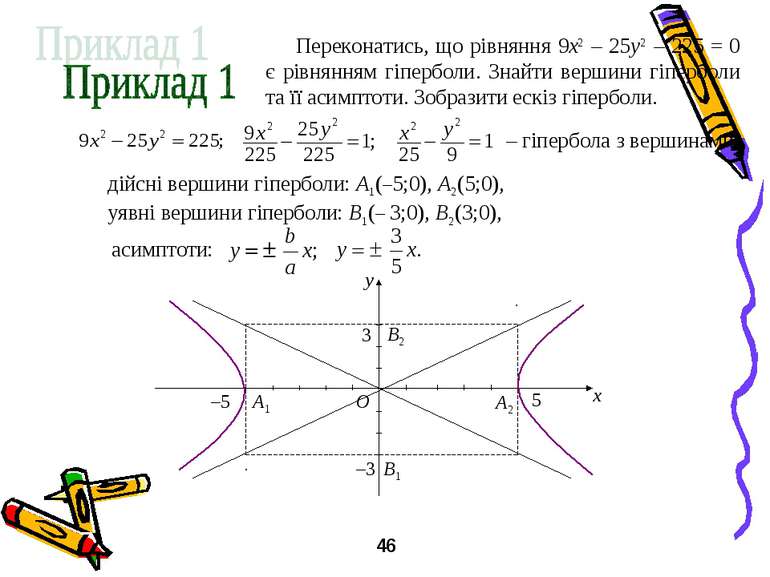
Переконатись, що рівняння 9x2 – 25y2 – 225 = 0 є рівнянням гіперболи. Знайти вершини гіперболи та її асимптоти. Зобразити ескіз гіперболи. дійсні вершини гіперболи: A1(–5;0), A2(5;0), уявні вершини гіперболи: B1(– 3;0), B2(3;0), – гіпербола з вершинами: асимптоти: y x O A1 A2 B1 B2 3 –3 –5 5 46

, Скласти рівняння гіперболи з фокусами на осі , якщо її дійсна вісь дорівнює 16, а уявна 8. Розв’язання: Приклад 2. Для складання рівняння гіперболи треба знати параметри і . З умови маємо , , і , . Підставивши ці значення в рівняння гіперболи , дістанемо:

2.5 Парабола з вершиною в початку координат Параболою називається множина точок , для кожної з яких відстань до деякої фіксованої точки площини, що називається фокусом, дорівнює відстані до деякої фіксованої прямої, яка не проходить через фокус і називається директрисою. Відстань від фокуса параболи до її директриси називається параметром параболи. Якщо осі декартової прямокутної системи координат вибрано так, що фокус міститься в точці , а директриса перпендикулярна до осі має рівняння , то рівняння параболи має вигляд:

Парабола має одну вісь симетрії, вісь симетрії параболи називається віссю параболи. Точка перетину параболи з віссю симетрії називається її вершиною. Для нашої параболи віссю є вісь , а вершиною – початок координат. Фокальний радіус довільної точки параболи ( тобто довжина ) відрізка може бути обчислений за формулою: де - абсциса точки . Якщо директриса параболи – пряма , а фокус – точка рівняння параболи має вигляд У випадку, якщо директриса параболи – пряма а фокус – точка рівняння параболи має вигляд: .

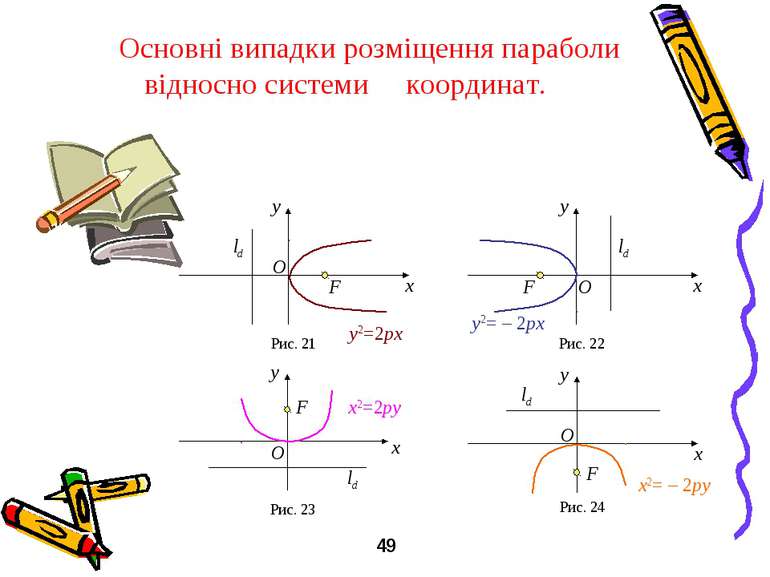
Основні випадки розміщення параболи відносно системи координат. y x F O ld Рис. 21 y2=2px y x F O ld Рис. 22 y2= – 2px y x F O ld Рис. 23 x2=2py y x F O ld Рис. 24 x2= – 2py 49

Приклад 1. Скласти рівняння параболи з вершиною в початку координат, якщо її фокус лежить у точці . Розв’язання : Фокус параболи лежить на додатній півосі , отже, рівняння параболи має вигляд , Оскільки координати фокуса , то , , звідки Підставивши значення в рівняння , дістанемо :

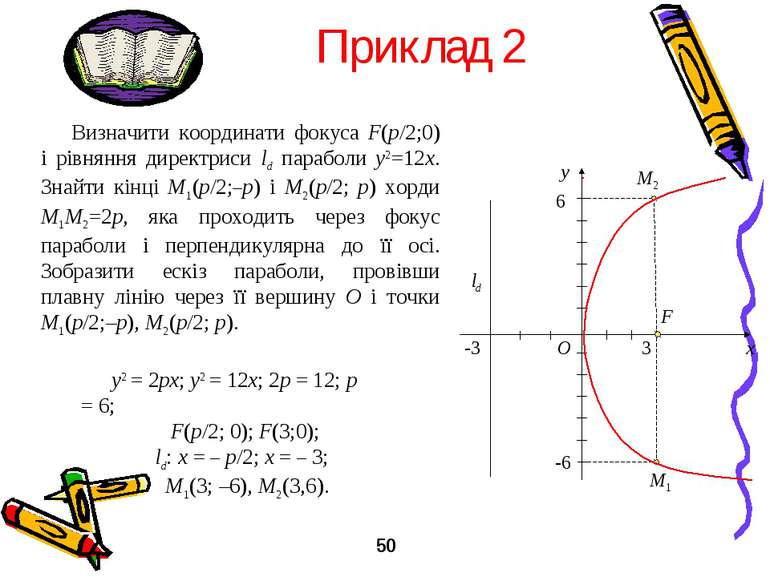
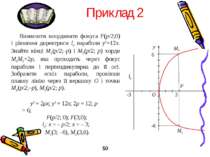
Приклад 2 Визначити координати фокуса F(p/2;0) і рівняння директриси ld параболи y2=12x. Знайти кінці M1(p/2;–p) і M2(p/2; p) хорди M1M2=2p, яка проходить через фокус параболи і перпендикулярна до її осі. Зобразити ескіз параболи, провівши плавну лінію через її вершину O і точки M1(p/2;–p), M2(p/2; p). y2 = 2px; y2 = 12x; 2p = 12; p = 6; F(p/2; 0); F(3;0); ld: x = – p/2; x = – 3; M1(3; –6), M2(3,6). y x O 3 6 -6 F ld M1 M2 -3 50

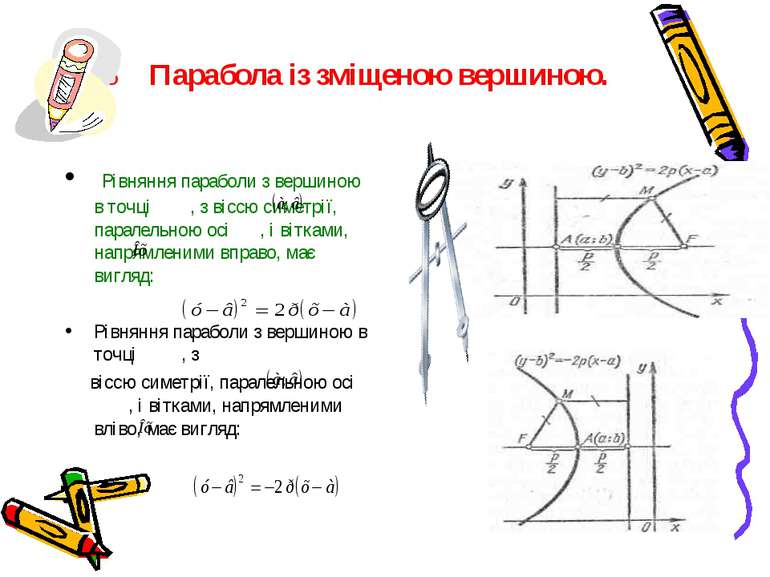
2.6 Парабола із зміщеною вершиною. Рівняння параболи з вершиною в точці , з віссю симетрії, паралельною осі , і вітками, напрямленими вправо, має вигляд: Рівняння параболи з вершиною в точці , з віссю симетрії, паралельною осі , і вітками, напрямленими вліво, має вигляд:

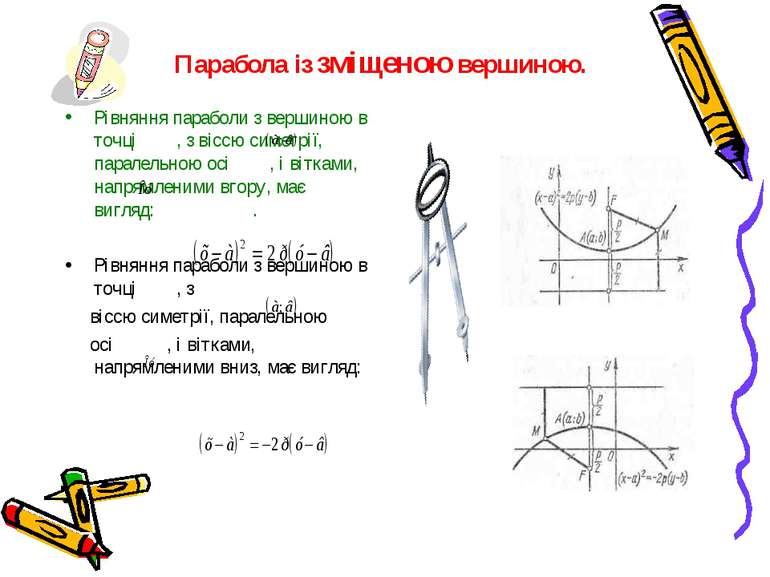
Парабола із зміщеною вершиною. Рівняння параболи з вершиною в точці , з віссю симетрії, паралельною осі , і вітками, напрямленими вгору, має вигляд: . Рівняння параболи з вершиною в точці , з віссю симетрії, паралельною осі , і вітками, напрямленими вниз, має вигляд:

Приклад 3. Дано рівняння параболи. Знайти координати її вершини. Розв’язання: Зведемо це рівняння до вигляду . Для цього зробимо перетворення : , ;