Презентація на тему:
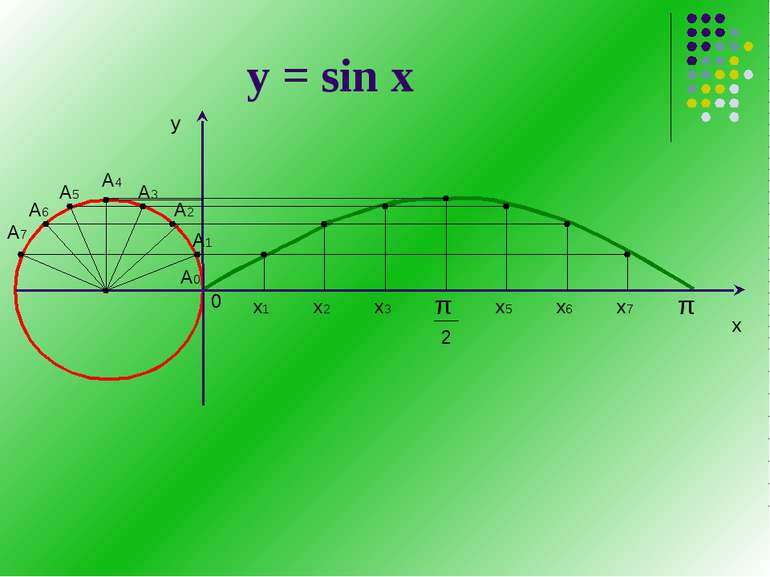
Графіки тригонометричних функцій

у = sin х А7

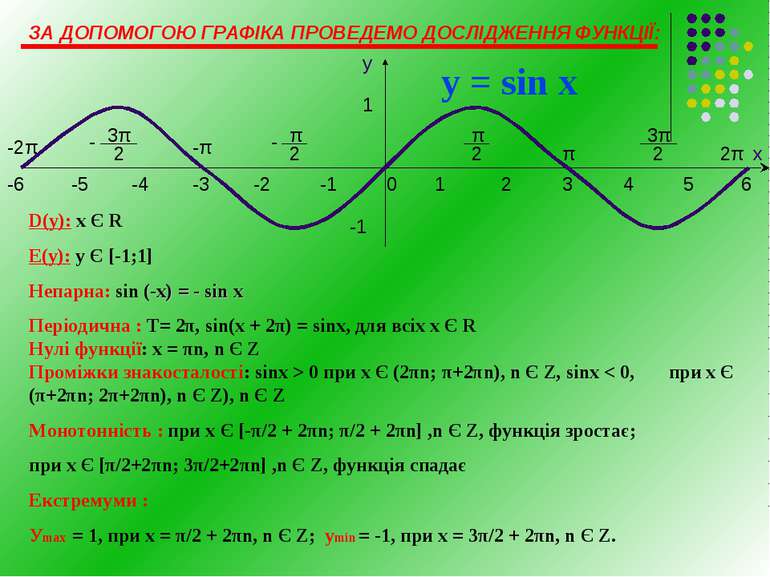
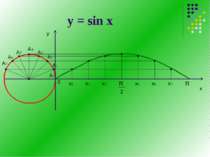
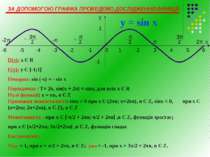
ЗА ДОПОМОГОЮ ГРАФІКА ПРОВЕДЕМО ДОСЛІДЖЕННЯ ФУНКЦІЇ: -6 у -2π D(y): х Є R Е(у): у Є [-1;1] Непарна: sin (-х) = - sin х Періодична : Т= 2π, sin(x + 2π) = sinx, для всіх х Є R Нулі функції: х = πn, n Є Z Проміжки знакосталості: sinx > 0 при x Є (2πn; π+2πn), n Є Z, sinx < 0, при x Є (π+2πn; 2π+2πn), n Є Z), n Є Z Монотонність : при x Є [-π/2 + 2πn; π/2 + 2πn] ,n Є Z, функція зростає; при x Є [π/2+2πn; 3π/2+2πn] ,n Є Z, функція спадає Екстремуми : Уmax = 1, при х = π/2 + 2πn, n Є Z; уmіn = -1, при х = 3π/2 + 2πn, n Є Z.

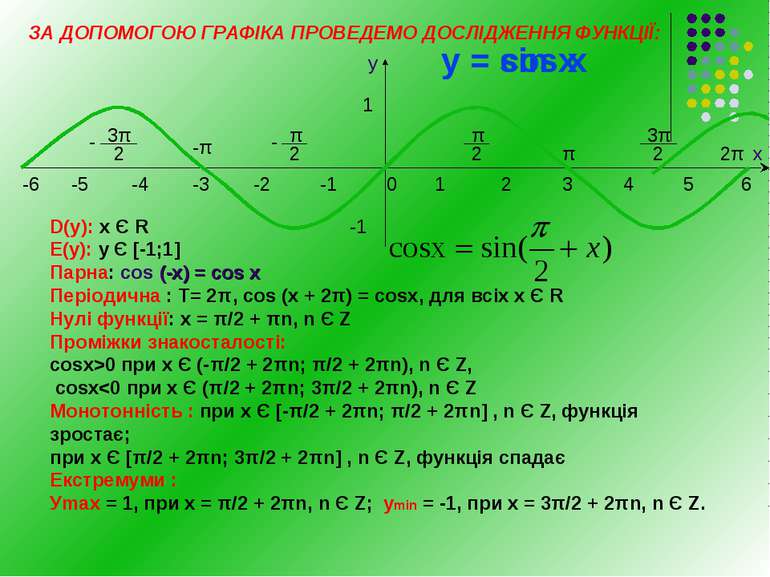
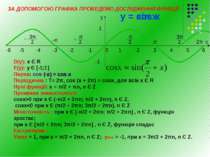
1 2 3 4 5 -1 -2 -3 -4 -5 6 0 х -1 1 π 2π - -π - у = sin х -6 у = соs х ЗА ДОПОМОГОЮ ГРАФІКА ПРОВЕДЕМО ДОСЛІДЖЕННЯ ФУНКЦІЇ: у D(y): х Є R Е(у): у Є [-1;1] Парна: cos (-х) = cos х Періодична : Т= 2π, cos (x + 2π) = cosх, для всіх х Є R Нулі функції: х = π/2 + πn, n Є Z Проміжки знакосталості: cosx>0 при x Є (-π/2 + 2πn; π/2 + 2πn), n Є Z, cosx

у х 0 х1 х2 х3 А0 А1 А2 А4 А3 01

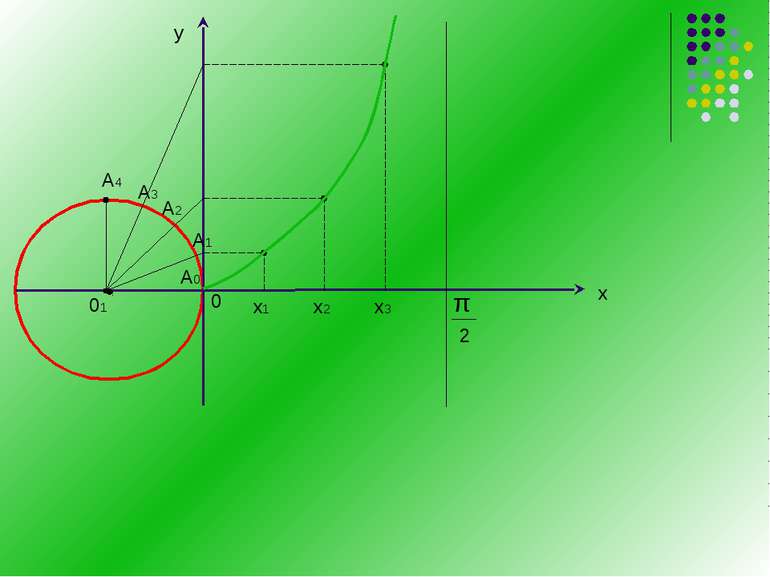
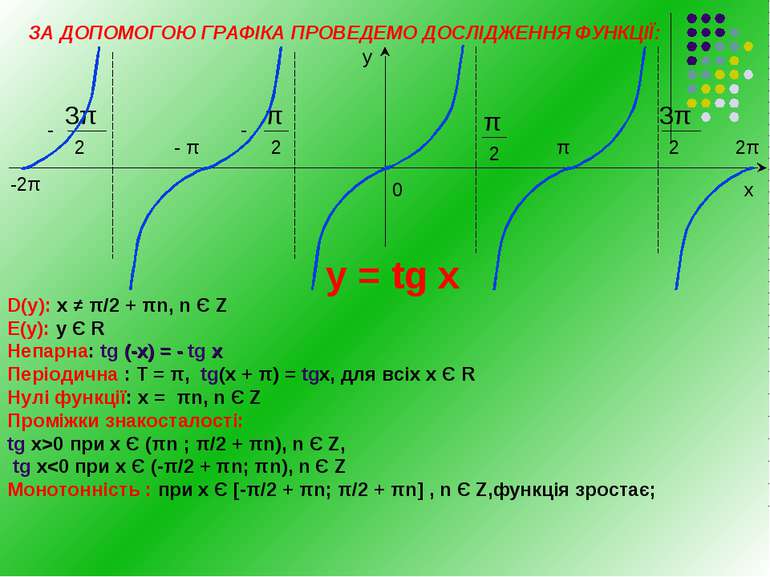
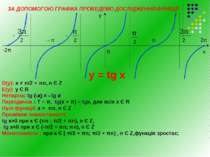
2π π π - - - 0 -2π х у ЗА ДОПОМОГОЮ ГРАФІКА ПРОВЕДЕМО ДОСЛІДЖЕННЯ ФУНКЦІЇ: у = tg х D(y): х ≠ π/2 + πn, n Є Z Е(у): у Є R Непарна: tg (-х) = - tg х Періодична : Т = π, tg(x + π) = tgх, для всіх х Є R Нулі функції: х = πn, n Є Z Проміжки знакосталості: tg x>0 при x Є (πn ; π/2 + πn), n Є Z, tg x

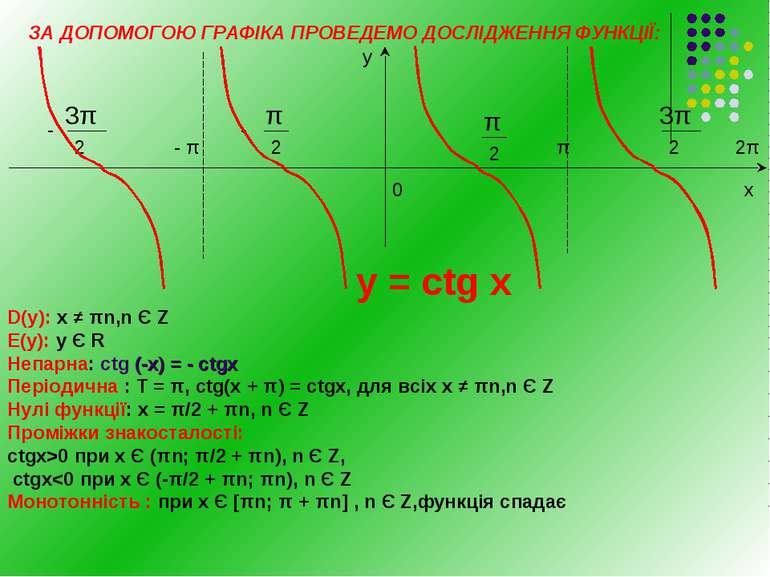
ЗА ДОПОМОГОЮ ГРАФІКА ПРОВЕДЕМО ДОСЛІДЖЕННЯ ФУНКЦІЇ: 2π π π - - - 0 х у у = сtg х D(y): х ≠ πn,n Є Z Е(у): у Є R Непарна: ctg (-х) = - ctgх Періодична : Т = π, ctg(x + π) = ctgх, для всіх х ≠ πn,n Є Z Нулі функції: х = π/2 + πn, n Є Z Проміжки знакосталості: ctgx>0 при x Є (πn; π/2 + πn), n Є Z, ctgx

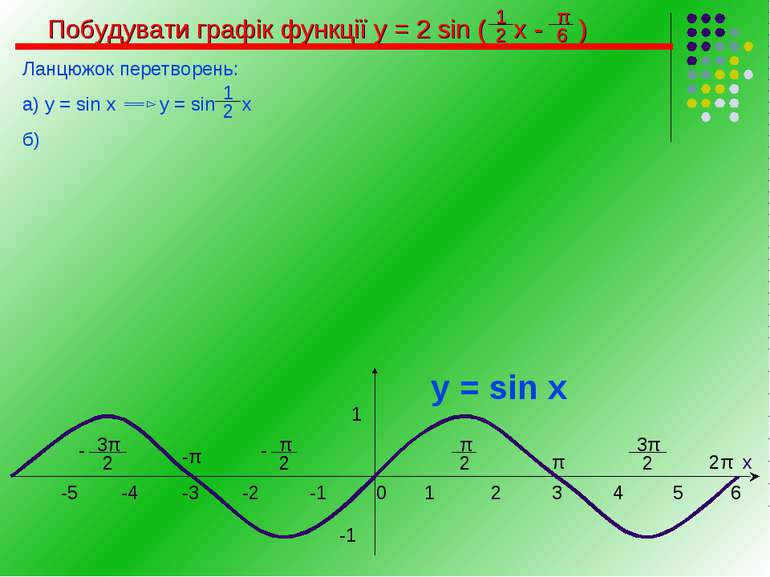
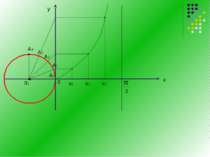
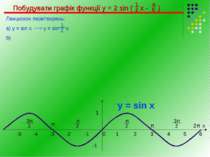
Побудувати графік функції у = 2 sin ( х - ) Ланцюжок перетворень: а) у = sin x у = sin х б) 6 х