Презентація на тему:
Тригонометричні функції,їх графіки і властивості

Тригонометричні функції, їх графіки і властивості Робота старшого вчителя, вчителя математики вищої категорії СЗШ І-ІІІ ступенів № 8 м. Хмельницького Тичинської Тетяни Іванівни

Функція y = sin x Графік функції y = sin x Властивості функції: D(sin x) = R y = sin x – непарна функція, графік симетричний відносно початку координат 3. періодичність: T = 2π 4. sin x = O при х = πn, n Z (нулі функції) 5. проміжки знакосталості: sin x > 0 при 0 + 2πn < x < π+ 2πn, n Z sin x < 0 при π + 2πn < x < 2π+ 2πn, n Z 6. проміжки монотонності: x [- π /2 + 2πn; π /2 + 2πn], n Z – зростає x [ π /2 + 2πn; 3π /2 + 2πn], n Z– спадає 7. екстремуми: y max = 1 при х = π /2 + 2πn, n Z y min = - 1 при х = - π /2 + 2πn, n Z 8. E(sin x) = [- 1 ; 1] 9. похідна: (sin x )´ = cos x

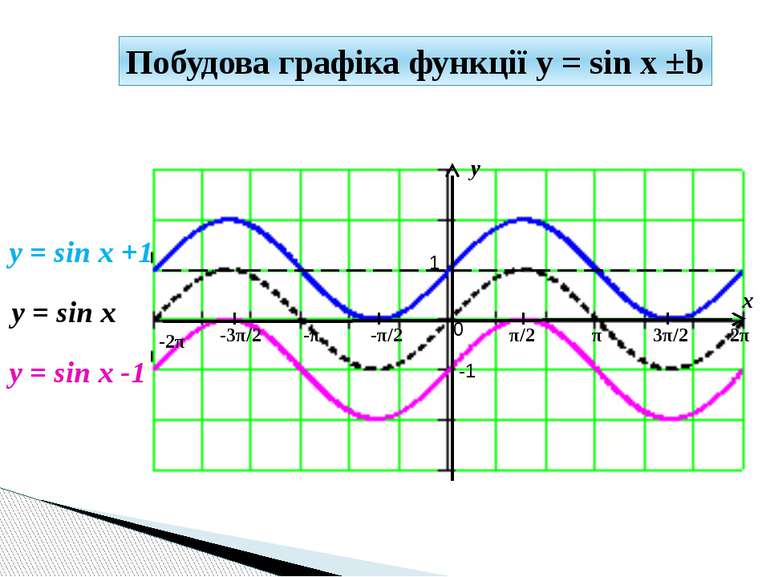
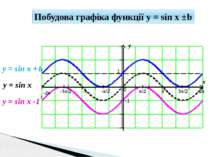
y x 1 -1 π/2 -π/2 π 3π/2 2π -π -3π/2 -2π 0 y = sin x +1 y = sin x Побудова графіка функції y = sin x ±b y = sin x -1

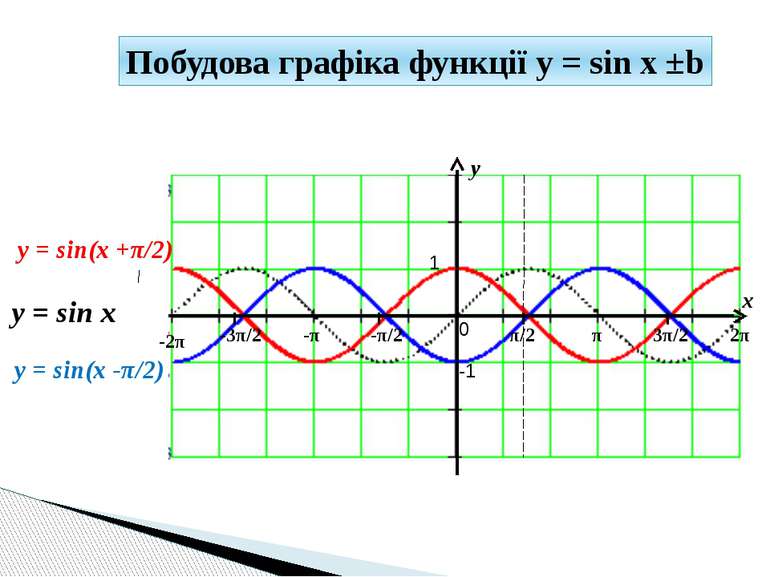
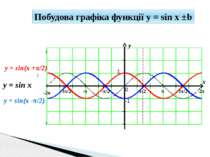
y x 1 -1 π/2 -π/2 π 3π/2 2π -π -3π/2 -2π 0 y = sin(x +π/2) y = sin x Побудова графіка функції y = sin x ±b y = sin(x -π/2)

Функція y = cos x Графік функції y = cos x Властивості функції: D(cos x) = R y = cos x –парна функція, графік симетричний відносно осі ординат 3. періодичність: T = 2π 4. cos x = 0 при х = π /2 + πn, n Z (нулі функції) 5. проміжки знакосталості cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, n Z cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, n Z 6. проміжки монотонності: x [ π+ 2πn; 2π+ 2πn], n Z –зростає x [0 + 2πn; π+ 2πn], n Z– спадає 7. екстремуми: y max = 1 при х = 2πn, n Z y min = - 1 при х = π+ 2πn, n Z 8. E(cos x) = [- 1 ; 1] 9. похідна: (cos x )´ = - sin x

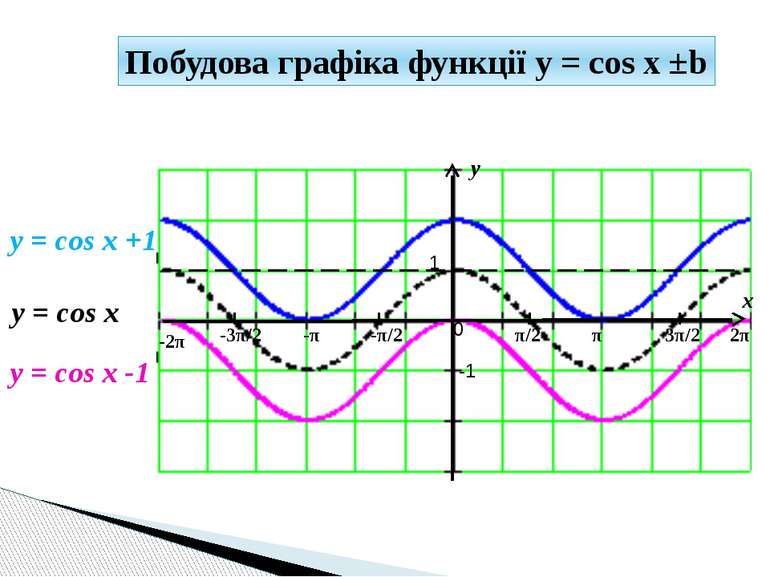
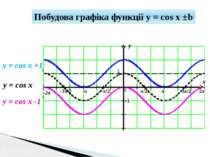
y x 1 -1 π/2 -π/2 π 3π/2 2π -π -3π/2 -2π 0 y = cos x +1 y = cos x Побудова графіка функції y = cos x ±b y = cos x -1

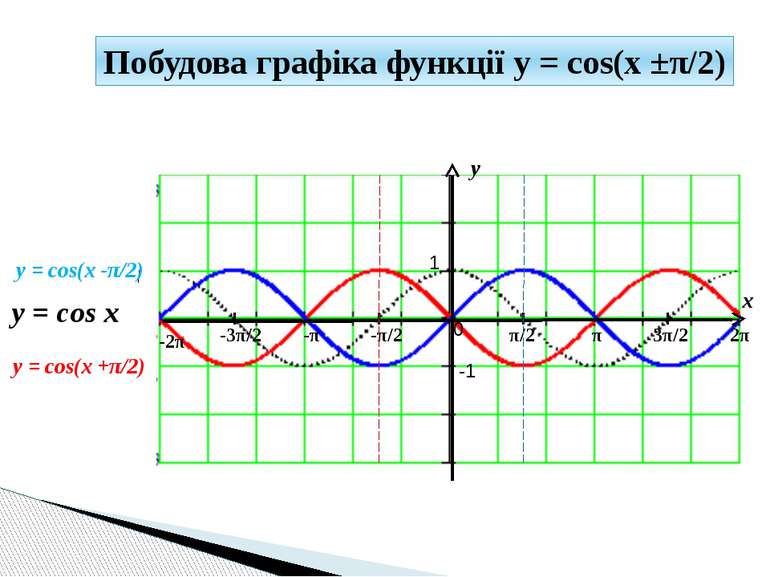
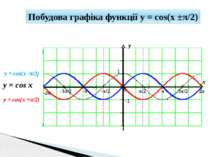
y x 1 -1 π/2 -π/2 π 3π/2 2π -π -3π/2 -2π 0 y = cos(x -π/2) y = cos x Побудова графіка функції y = cos(x ±π/2) y = cos(x +π/2)

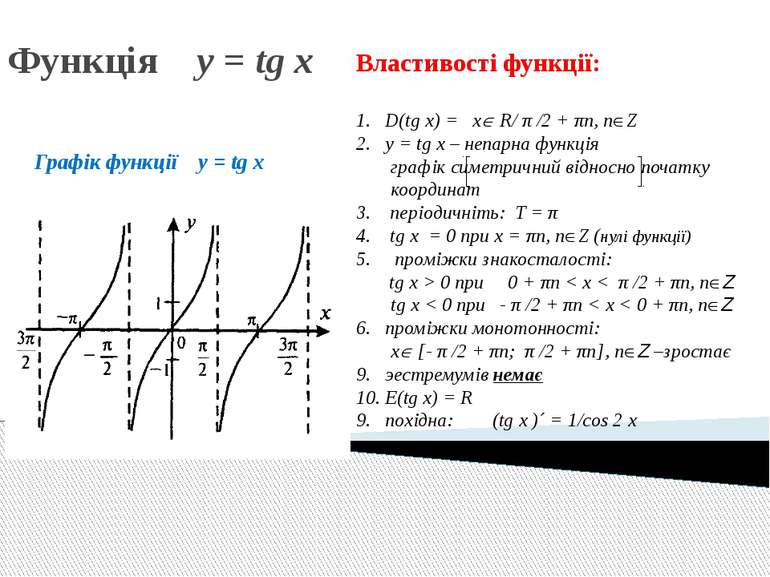
Функція y = tg x Графік функції y = tg x Властивості функції: D(tg x) = x R/ π /2 + πn, n Z y = tg x – непарна функція графік симетричний відносно початку координат 3. періодичніть: T = π 4. tg x = 0 при х = πn, n Z (нулі функції) 5. проміжки знакосталості: tg x > 0 при 0 + πn < x < π /2 + πn, n Z tg x < 0 при - π /2 + πn < x < 0 + πn, n Z 6. проміжки монотонності: x [- π /2 + πn; π /2 + πn], n Z –зростає эестремумів немає E(tg x) = R 9. похідна: (tg x )´ = 1/cos 2 x

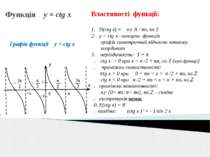
Функція y = ctg x Графік функції y = ctg x Властивості функції: D(ctg x) = x R / πn, n Z y = ctg x –непарна функція графік симетричний відносно початку координат 3. періодичність: T = π 4. ctg x = 0 при х = π /2 + πn, n Z (нулі функції) 5. проміжки знакосталості: ctg x > 0 при 0 + πn < x < π /2 + πn, n Z ctg x < 0 при π /2 + πn < x < π + πn, n Z 6. проміжки монотонності: x [0+ πn; π+ πn], n Z – спадає екстремумів немає E(ctg x) = R 9. похідна: (ctg x )´ = - 1/sin 2 x