Презентація на тему:
Найпростіші тригонометричні рівняння

Якщо результат не залежить від способу розв’язування – це математика, а якщо залежить – це бухгалтерія.

Перевір себе А) Б) В) Г) Д)

Тема заняття Найпростіші тригонометричні рівняння

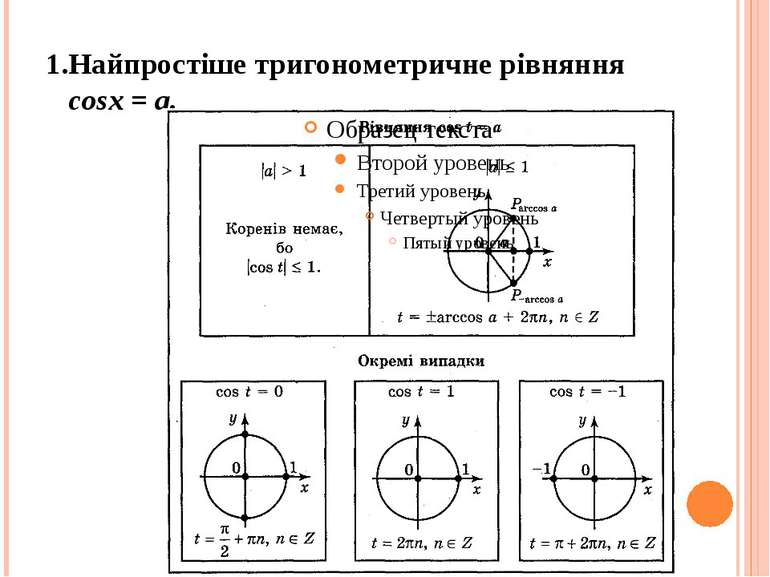
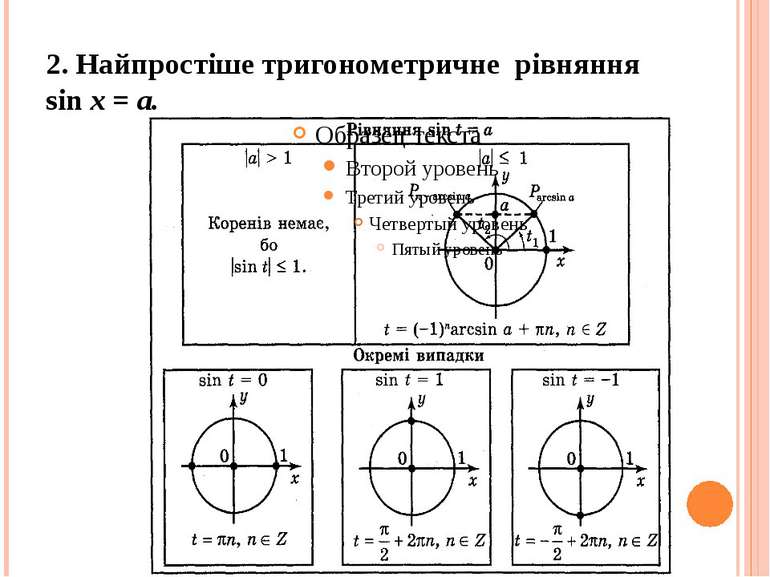
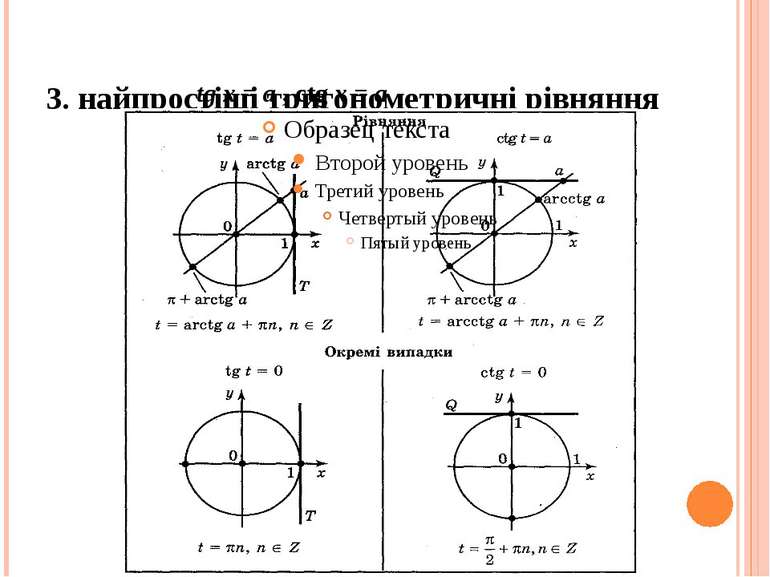
План заняття 1.Найпростіше тригонометричне рівняння cos x = a . Тренувальні вправи. 2.Найпростіше тригонометричне рівняння sin x = a. Тренувальні вправи. 3. Найпростіші тригонометричні рівняння tg x = a, ctg x = a. Тренувальні вправи. 4. Розв’язування різних типів найпростішиx тригонометричних рівнянь.

Геометрія. Розв’язування трикутників Найпростіші тригонометричні рівняння Вища математика. Диференціальні рівняння Вища математика. Аналітична геометрія

БЛІЦ - ОПИТУВАННЯ

1. Яка функція називається оборотною? Функція f називається оборотною на деякому проміжку якщо на цьому проміжку до неї існує обернена

2. Необхідна умова оборотності функції. Для того щоб функція була оборотною, необхідно щоб вона кожне своє значення приймала лише раз на області визначення.

3. Достатня умова оборотності функції. Для того, щоб функція була оборотною, достатньо щоб вона була монотонною (зростаюча або спадна )

4.Чи задовольняють умови оборотності тригонометричні функції для довільних значень змінної x ? Ні. Оскільки не виконується необхідна умова оборотності

5. Як ми вирішуємо цю проблему? Розглядаємо дані функції на окремому інтервалі, де виконуються необхідна та достатня умови оборотності.

6.Що називається арксинусом числа a? Арксинусом числа а називається таке число із проміжку синус якого дорівнює а.

7. Що таке арккосинус числа а? Чому дорівнює арккосинус від’ємного аргументу? Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а. arccos (-а) = π - arccos а.

8.Що таке арктангенс числа a ? Арктангенсом числа а називається таке число з проміжку , тангенс якого дорівнює а.

9.Що таке арккотангенс числа a ? Чому дорівнює арккотангенс від’ємного аргументу? Арккотангенсом числа а називається таке число із інтервалу (0; π), котангенс якого дорівнює а. arcctg (-а) = π - arcctg а

МАТЕМАТИЧНИЙ ДИКТАНТ

Варіант -1 Варіант -2 1) arcsin 1; 1) arccos 2) arcsin 2) arccos 3) arcsin 0 3) arсcos (-l) 4) arccos 4) arccos 5) arcsin 5) arctg 6) arcctg 1; 6) arctg 7) arсtg 0; 7) arcctg 8) arcctg(- ) 8) arctg1

Відповіді Варіант -1 Варіант -2 1) 2) ; 3) 0 4) 5) - 6) 7) 0; 8) 1) 2) 3) ; 4) 5) 6) 7) 8)

1.Найпростіше тригонометричне рівняння cosx = а.

2. Найпростіше тригонометричне рівняння sin x = a.

3. найпростіші тригонометричні рівняння tg x = a , ctg x = a

Алгоритм розв’язування найпростішого тригонометричного рівняння Визначити тип рівняння. (cosx = а, sinx = а, tgx = а чи ctgx = а). Якщо це один із двох перших типів, то з’ясувати загальний чи окремий випадок. Застосувати відповідну формулу