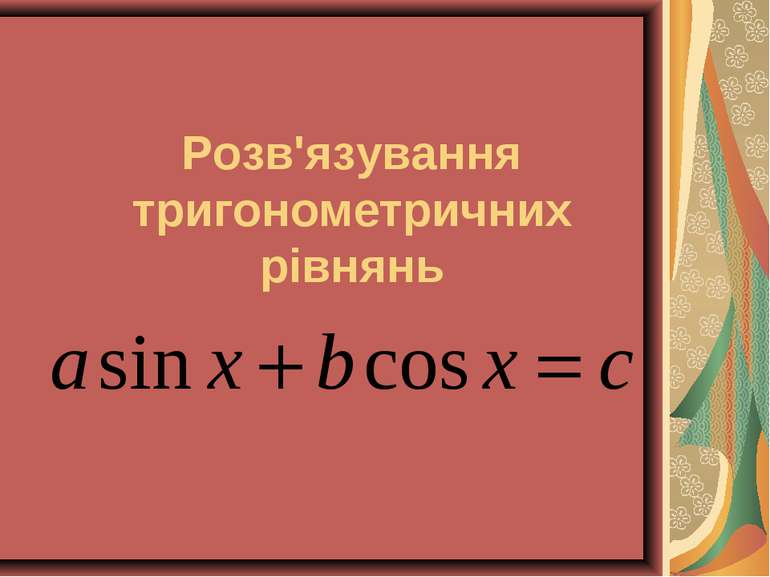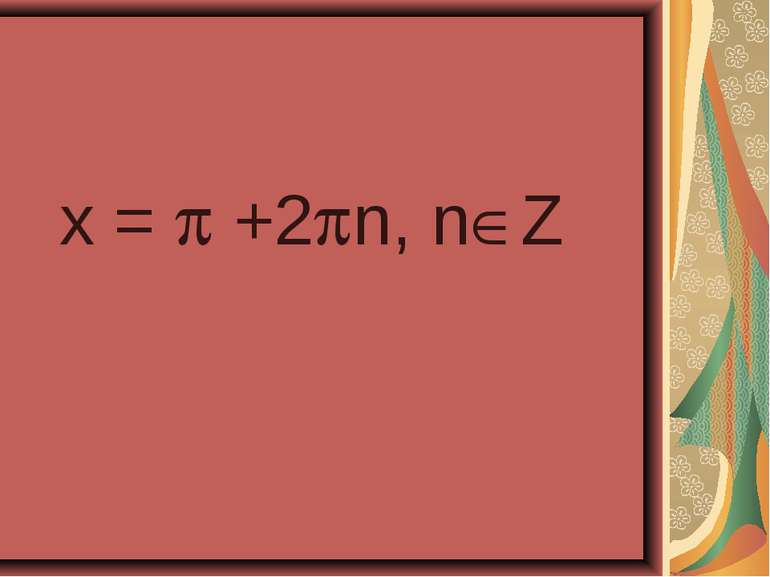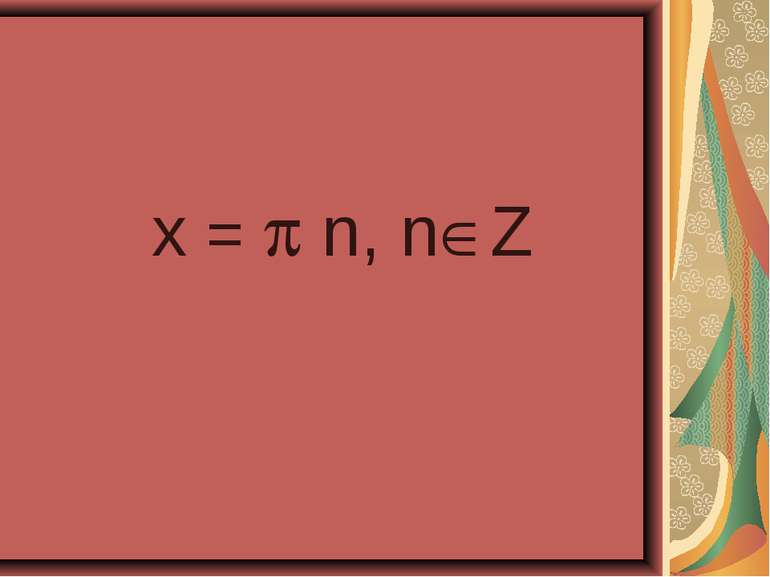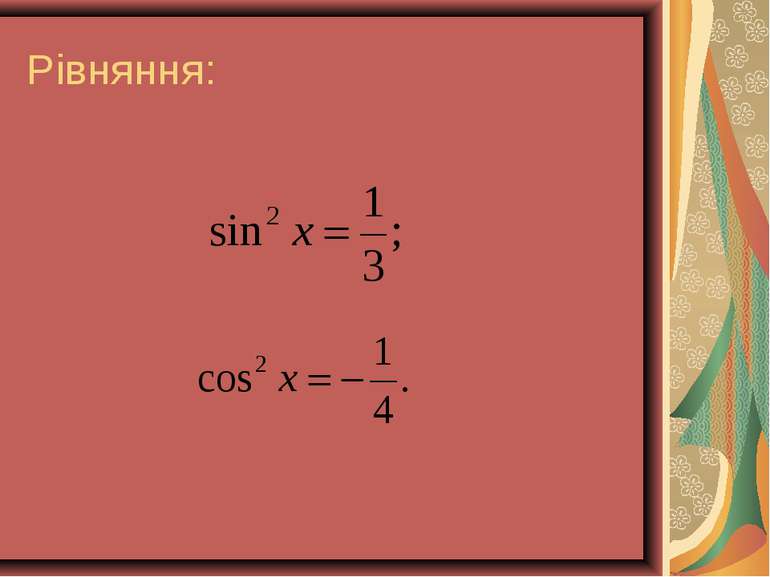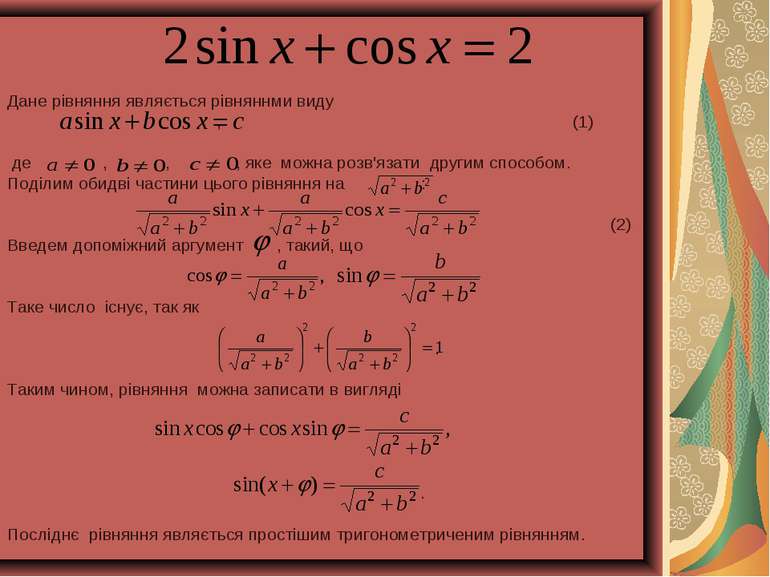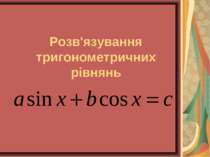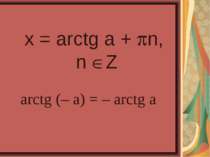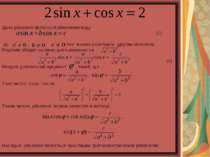Презентація на тему:
Розв'язування тригонометричних рівнянь

Розв'язування тригонометричних рівнянь

Мета уроку: Створення умов для засвоєння знань і умінь розв'язувати тригонометричні рівняння виду a sinx + b cosx = c. Формування новичок самоконтролю і взаємоконтролю, алгоритмічної культури учнів. Развиток усної математичної мови . Удосконалювати уміння старшокласників: порівнювати,аналізувати, развивати навички обробки інформації. Развивати комунікативні уміння ділового спілкування однолітків. Виховання культури записів.

Перевірка домашнього завдання sin7x – sin x =cos4x

Розв'язання . sin7x – sin x =cos4x, 2sin3x cos4x - cos4x =0, сos4x ( 2sin3x – 1 )=0, сos4x=0 или 2cos3x -1 =0 сos4x=0 4x =П/2+Пn, n € Z; cos3x =1/2, X=П/8 +Пn/4, n € Z, 3x =±аrccos1/2 +2Пn, n 3x =±П/3 +2Пn, n € Z, X =±П/9 + 2/3Пn, n € Z. Відповідь: X=П/8 +Пn/4, X =±П/9 = 2/3Пn, n € Z

Розв'язати рівняння sin²x - cos²x = cos4x

Розв'язання . sin²x-cos²x =cos4x , - (cos² - sin²x )=cos4x , -cos2x = cos²2x - sin²2x, -cos2x = cos²2x – ( 1 - cos²2x), -cos2x - cos²2x +1 - cos²2x = 0, -2cos²2x – cos2x +1 = 0, 2cos²2x + cos2x -1 = 0. Заміним сos2x на У , де |У| 1 Тоді 2 у² +у -1 = 0, D =1 - 4•2•(-1) =9, У =1/ 2, у = -1. Виконаємо обернену заміну Cos2x =1/ 2 , cos2x = -1, 2x = П+2Пn, n € Z, 2x =±arccos1/2 =2Пn , n € Z, x=П/2+Пn, n € Z. 2x ±П/3 +2Пn. n € Z, X =±П/6+Пn, n € Z. Відповідь : X =±П/6+Пn, x=П/2+Пn, n € Z.

Розв'язати рівняння з підручника №2 (1) №2 (8)

COS X = a, де|a| 1

x = arccos a + 2 n, n Z arccos (– a) = - arccos a

sin X = a, де|a| 1

x=(–1)narcsin a + n, n Z arcsin (– a) = – arcsin a

tg x = a, де a R

x = arctg a + n, n Z arctg (– a) = – arctg a

cos x = 0

x = + n, n Z

cos x = 1

x = +2 n, n Z

cos x = -1

x = +2 n, n Z

sin x=0

x = n, n Z

sin x=1

x = +2 n, n Z

sin x = -1

x = - +2 n, n Z

Розв'язати рівняння 4sin²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0

Відповіді. 4sin²x - 4 sinx – 3 = 0 ( -1)n+1 П/6 +Пn, n Z. 2 сos²x – sin x – 1 = 0 ±П/6 +Пn; -П/2+2Пn, n Z.

Рівняння:

Рівняння:

Рівняння . Рівняння . Поділивши рівняння на , одержимо , , При розвязанні цієї задачі обидві частини рівняння були поділені на . Нагадаємо, що при ділені рівняння на вираз, який містить невідоме, можуть бути втрачені корені. Тому необхідно перевірити,чи неявляються корені рівняння коренями даного рівняння . Якщо , то із рівняння слідуєт, що . Але і не можуть одночасно дорівнювать нулю, так як вони зв'язані рівністю . Отже , при діленні рівняння де , , на (або ) одержуємо рівняння , рівносильне даному.

Рівняння . Використовуючи формули sin x = 2 sin cos , cos x = cos2 - sin2 і записуючи праву частину рівняння в вигляді, одержуємо Поділивши це рівняння на , Одержуємо рівносильне рівняння Позначимо , одержуєм , звідки . 1) 2) Відповідь:

Дане рівняння являється рівняннми виду , (1) де , , , яке можна розв'язати другим способом. Поділим обидві частини цього рівняння на : . (2) Введем допоміжний аргумент , такий, що . Таке число існує, так як . Таким чином, рівняння можна записати в вигляді . Посліднє рівняння являється простішим тригонометриченим рівнянням.

Розв'язати рівняння

Розв'язати рівняння Тут Поділимо обидві частини рівняння на 5: Введем допоміжний аргумент , такий, що , . Початкове рівняння можна записати в вигляді , , звідки Відповідь: