Презентація на тему:
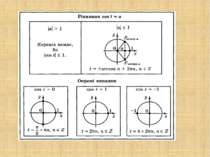
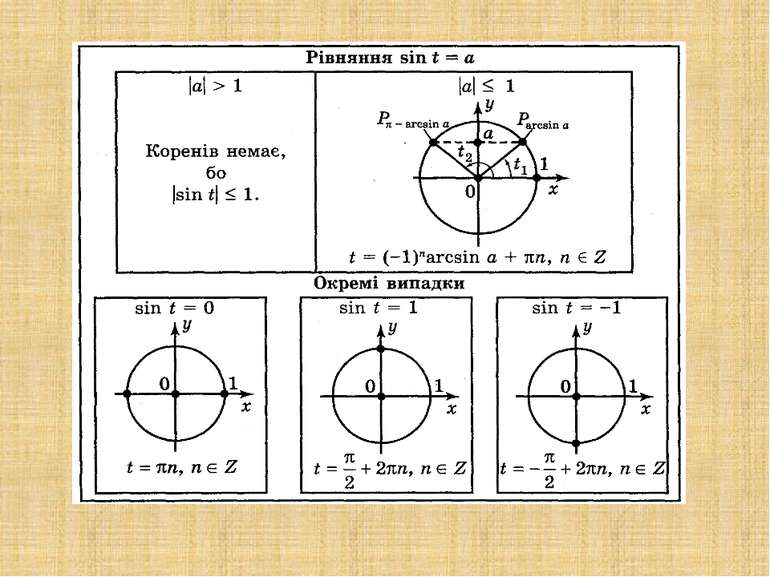
Розв’язування найпростіших тригонометричних нерівностей

У світі гармонічних коливань. Тригонометричні функції та їх властивості. Розв'язування найпростіших тригонометричних рівнянь Лисогор Таміла Веніамінівна вчитель математики Стебненської загальноосвітньої школи І-ІІІ ст. Звенигородської районної ради Черкаської області

ТЕМА УРОКУ У світі гармонічних коливань. Тригонометричні функції та їх властивості. Розв'язування найпростіших тригонометричних рівнянь

Мета : вміти застосовувати здобуті знання в нестандартних умовах, аналізувати та систематизувати здобуті знання, дослідити закони синусоїди та косинусоїди в навколишньому світі, сформувати вміння застосовувати означення та властивості обернених тригонометричних функцій при розв'язуванні найпростіших тригонометричних рівнянь

Епіграф Природа формує свої закони мовою математики Г.Галілей

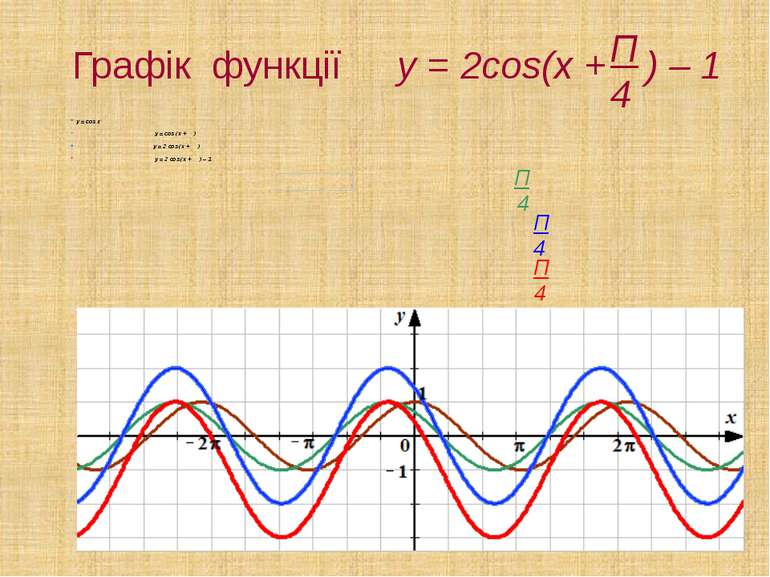
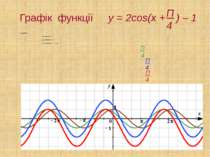
Графік функції y = 2cos(x + ) – 1 y = cos x y = cos (x + ) y = 2 cos (x + ) y = 2 cos (x + ) – 1 Π 4 Π 4 Π 4 Π 4

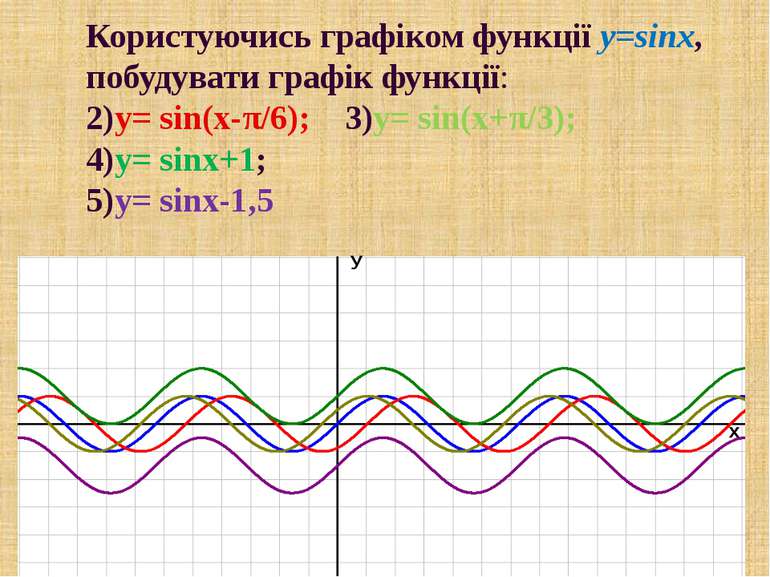
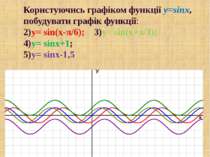
Користуючись графіком функції y=sinx, побудувати графік функції: 2)y= sin(x-π/6); 3)y= sin(x+π/3); 4)y= sinx+1; 5)y= sinx-1,5   У х

Леонард Ейлер великий вчений XVIII ст.

ГАРМОНІКИ В ПРИРОДІ

Періодичні зміни фізичної величини в залежності від часу, які відбуваються за законом синуса або косинуса називаються гармонічними коливаннями. Рівняння гармонічних коливань : . .

Гармонічні коливання математичного маятника

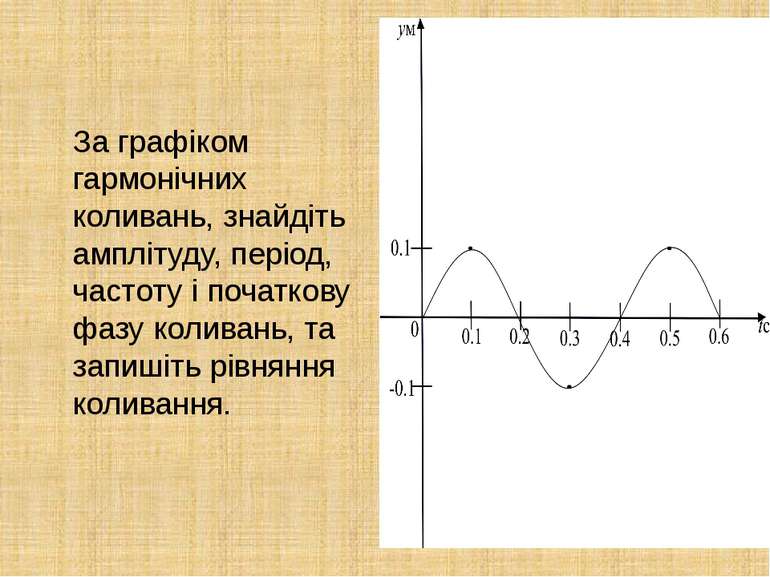
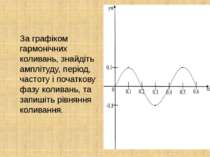
За графіком гармонічних коливань, знайдіть амплітуду, період, частоту і початкову фазу коливань, та запишіть рівняння коливання.

Графіки обернених тригонометричних функції

1. Область визначення у = sin x у = arcsin x [-1 ; 1] 2. Область значень [-1 ; 1] Функція непарна Неперіодична Нулі функції O(0;0) Функція зростаюча y > 0 при х є [0;1] y < 0 при х є [-1;0] arcsin x називається таке число з проміжку синус якого дорівнює х.

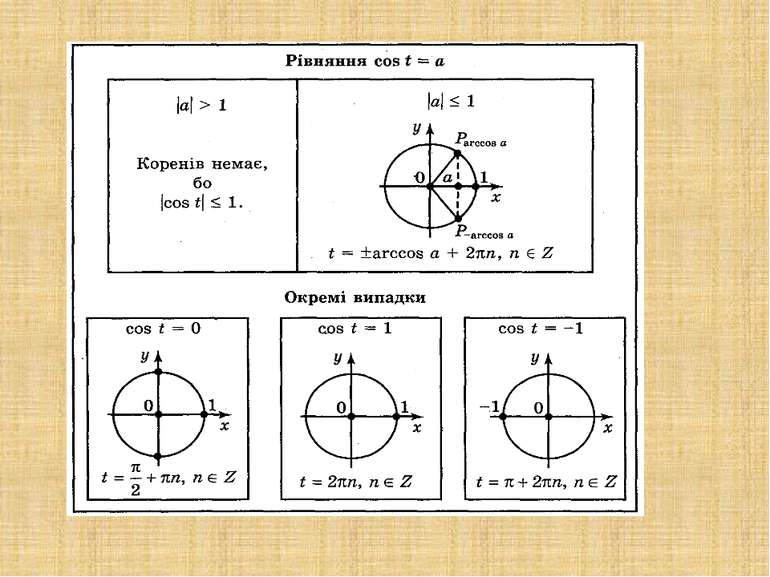
Функція ні парна ні непарна Функція спадає Функция неперіодична Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а. arccos (-а) = π - arccos а. arccos = x y

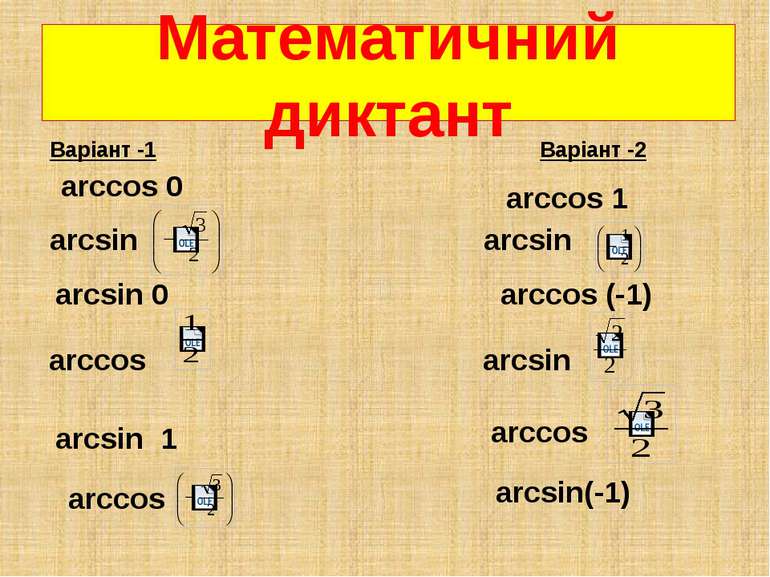
Математичний диктант Варіант -1 Варіант -2 аrcsin аrcsin аrcsin 0 аrcsin аrcsin 1 arccos 0 arccos 1 arccos (-1) arccos arccos аrcsin(-1) arccos

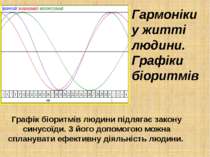
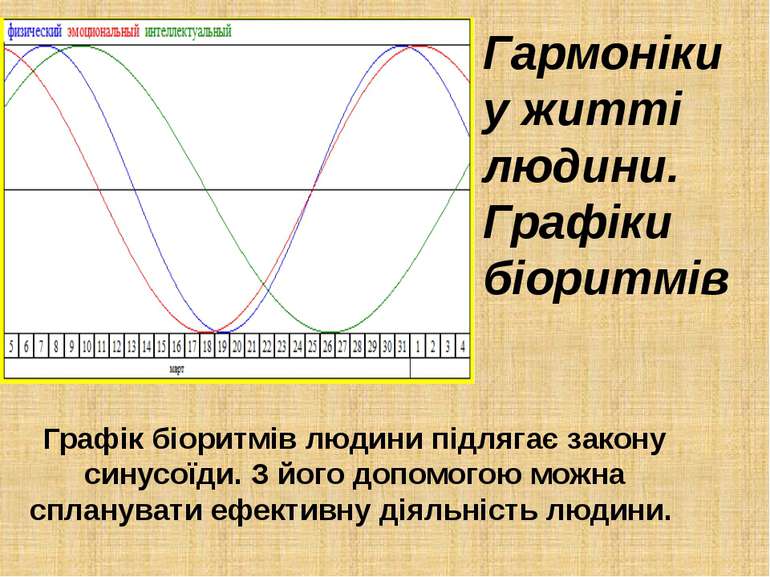
Гармоніки у житті людини. Графіки біоритмів Графік біоритмів людини підлягає закону синусоїди. З його допомогою можна спланувати ефективну діяльність людини.

Синус (від лат. sinus) – вигин, кривизна.

Домашнє завдання Є.П.Нелін. §24, стор. 324 -329, вправи № 10,11, стор. 334. Повт. Властивості функцій тангенса і котангенса.

ЛІТЕРАТУРА Програма для загальноосвітніх навчальних закладів. Математика. 10-11 кл.2010. Алгебра і початки аналізу: підруч. для 10 кл.загальноосвіт.навчальн.закладів: академ.рівень/Є.П.Нелін.-Х.:Гімназія,2010 Програма біоритми. http://youryoga.org/upload/programs Майстер функцій. Програма.