Презентація на тему:
Графік функції y=x2+n. Графік функції y=(x+m)2

Тема 3 Функція. Квадратична функція Поняття квадратичної функції. Графік функції y=x2+n. Графік функції y=(x+m)2 Графік функції y=(x+m)2+n. Графік функції y=ax2 Графік функції a(x+m)2+n Графік функції ax2+bx+c Властивості квадратичної функції Найпростіші перетворення графіків функцій Розв’язування вправ. Самостійна робота Розв'язування вправ

Пункт 3.2-3.3. Пригадайте До якого виду функції належить функція y=x2? Що є графіком функції y=x2? Як він розміщений на координатній площині? Графік функції y=x2+n Графік функції y=(x+m)2 Парабола

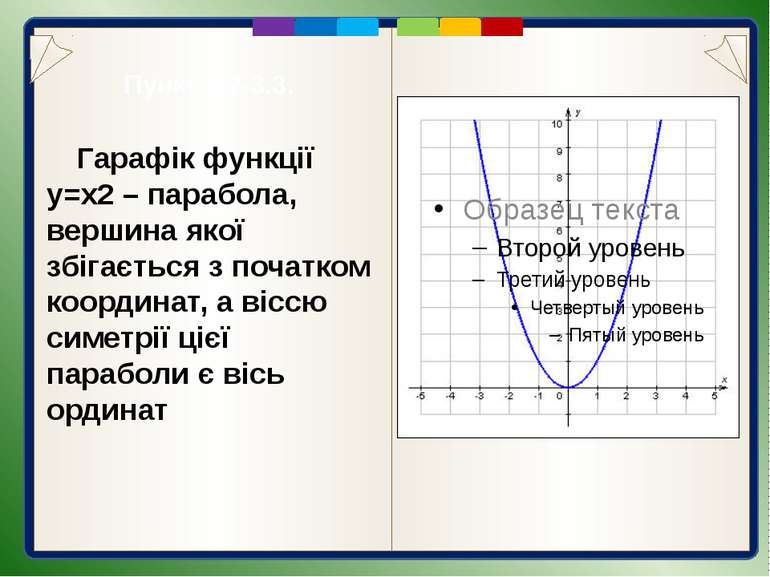
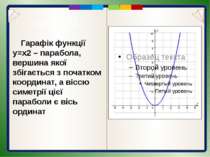
Пункт 3.2-3.3. Гарафік функції y=x2 – парабола, вершина якої збігається з початком координат, а віссю симетрії цієї параболи є вісь ординат

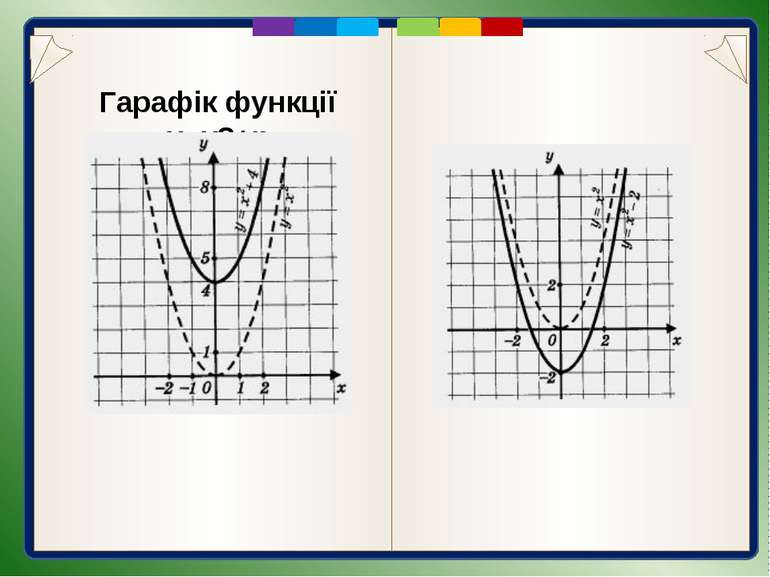
Пункт 3.2-3.3. Гарафік функції y=x2+2 Традиційний спосіб: 1). побудувати кілька точок графіка за їх координатами, які знаходять, надаючи змінній х певного значення і обчислюючи відповідне значення змінної у; 2). провести через побудовані точки криву.

Гарафік функції y=x2+2 2) Скориставшись побудованим уже графіком функції у = х2. Аналізуючи формули у = х2 і у = х2+2, зауважимо, що при одному і тому самому значенні х значення другої функції завжди на 2 більше від відповідного значення першої. Це означає, що кожна точка графіка функції у = х2 + 2 лежить на 2 одиниці вище від точки графіка функції у = х2 з тією самою абсцисою. Звідси випливає, що графік функції у = х2 + 2 можна отримати паралельним перенесенням графіка у = х2 вздовж осі ординат угору на 2 одиниці. Отже, графіком функції у = х2 + 2 також є парабола, вершина якої має координати (0; 2), а віссю симетрії є вісь ординат.

Гарафік функції y=x2-3 Графік функції у =х2-3 можна отримати за допомогою паралельного перенесення графіка функції у = х2 вздовж осі ординат (осі симетрії) вниз на 3 одиниці. Взагалі, графік функції у = х2 + n є параболою, яку отримують паралельним перенесенням графіка функції у = x2 на |n| одиниць вздовж осі Оу (осі симетрії) вгору, якщо n > 0, або вниз, якщо n< 0. Вершина цієї параболи має координати (0; n), а віссю симетрії графіка є вісь ординат.

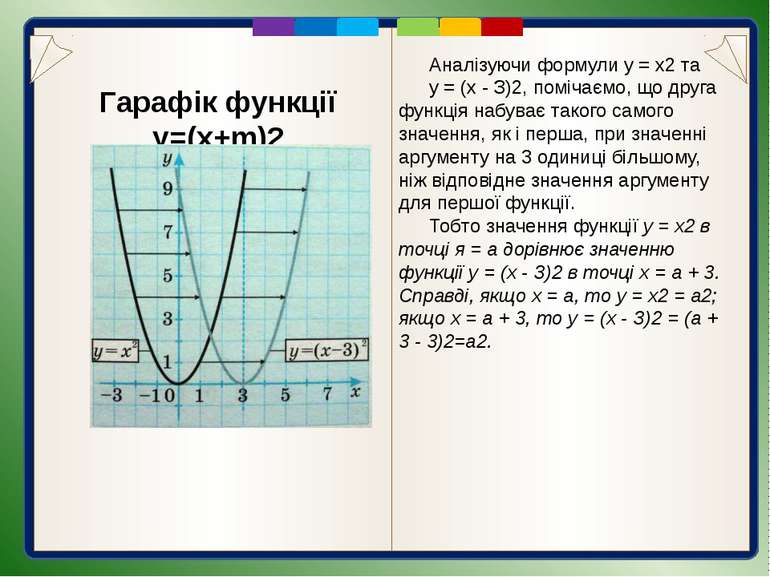
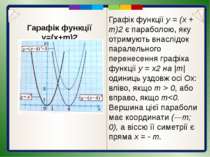
Гарафік функції y=(x+m)2 Аналізуючи формули у = х2 та у = (х - З)2, помічаємо, що друга функція набуває такого самого значення, як і перша, при значенні аргументу на 3 одиниці більшому, ніж відповідне значення аргументу для першої функції. Тобто значення функції у = х2 в точці я = а дорівнює значенню функції у = (х - З)2 в точці х = а + 3. Справді, якщо х = а, то у = х2 = а2; якщо х = а + 3, то у = (х - З)2 = (а + 3 - 3)2=а2.

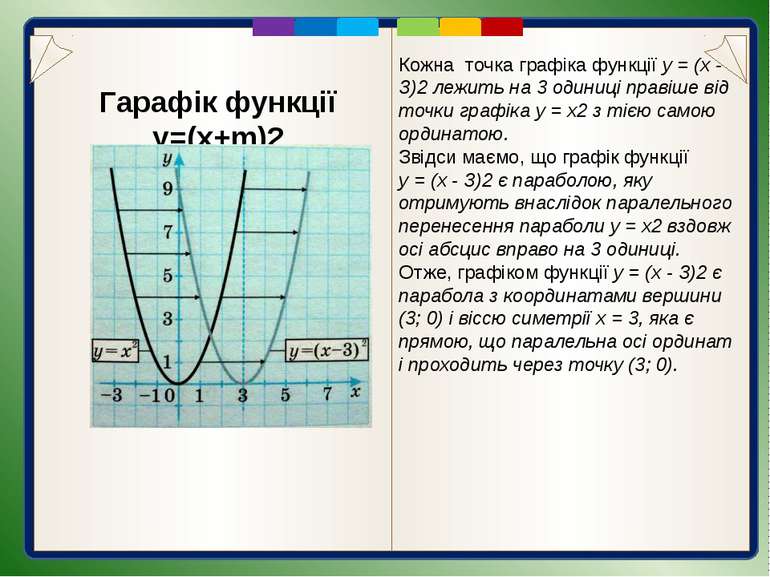
Гарафік функції y=(x+m)2 Кожна точка графіка функції у = (х - З)2 лежить на 3 одиниці правіше від точки графіка у = х2 з тією самою ординатою. Звідси маємо, що графік функції у = (х - З)2 є параболою, яку отримують внаслідок паралельного перенесення параболи у = х2 вздовж осі абсцис вправо на 3 одиниці. Отже, графіком функції у = (х - З)2 є парабола з координатами вершини (3; 0) і віссю симетрії х = 3, яка є прямою, що паралельна осі ординат і проходить через точку (3; 0).

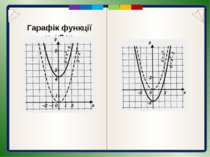
Гарафік функції y=(x+m)2 Графік функції у = (х + 2)2 можна отримати за допомогою паралельного перенесення параболи у = х2 вздовж осі абсцис вліво на 2 одиниці .

Гарафік функції y=(x+m)2 Графік функції у = (х + 2)2 можна отримати за допомогою паралельного перенесення параболи у = х2 вздовж осі абсцис вліво на 2 одиниці .

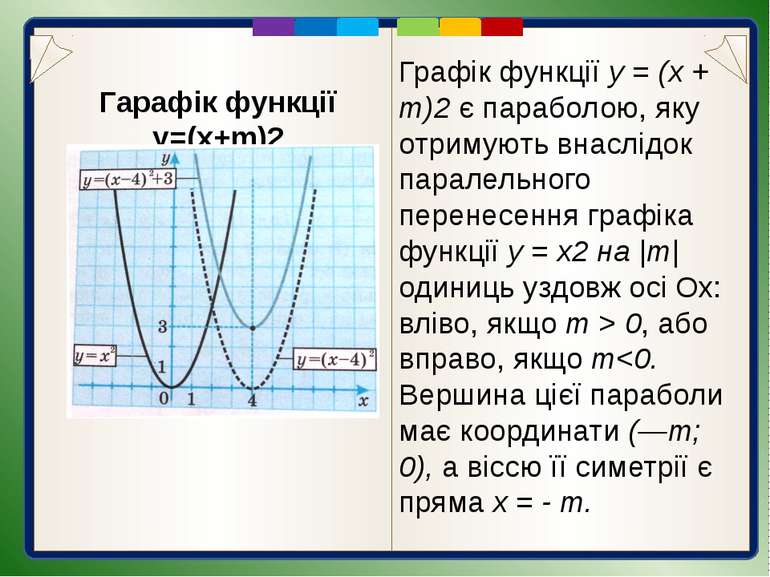
Гарафік функції y=(x+m)2 Графік функції у = (х + т)2 є параболою, яку отримують внаслідок паралельного перенесення графіка функції у = х2 на |т| одиниць уздовж осі Ох: вліво, якщо т > 0, або вправо, якщо т

Гарафік функції y=x2+n

Запитання для самоперевірки 1. Що є графіком функції виду у = (х + m)2? 2. Як обґрунтувати, що графік функції у = (х - 5)2 — пaрабола виду у = х 2? 3. В якій послідовності виконують побудову графіка функції виду = (х +m)2 ?