Презентація на тему:
Функції і їх графіки

Екстремуми функції. Найбільше і найменше значення функції зміст Загальні властивості функції Поняття зворотного функції Неперервність елементарні функції Поняття функції

Поняття функції Нехай D і E - непорожні числові множини, а x і y - відповідно їх елементи . Якщо кожному x,D ( x належить безлічі D ) ставиться , відповідно з деяким законом , тільки одне значення y,E , то говорять , що між змінними x і y існує функціональна залежність, і x називають незалежною змінною (або аргументом ) , а y - залежною змінною (або функцією ) .  Символічна запис функції: y = f ( x ) ( x,D , y,E ) . Безліч D називають областю визначення функції і позначають D ( f ) , а безліч E називають областю зміни функції - E ( f ) . Кажуть ще , що функція f відображає безліч D на безлічі E.

Загальні властивості функції Парність і непарність Періодичність Нулі функції Проміжки знакосталості

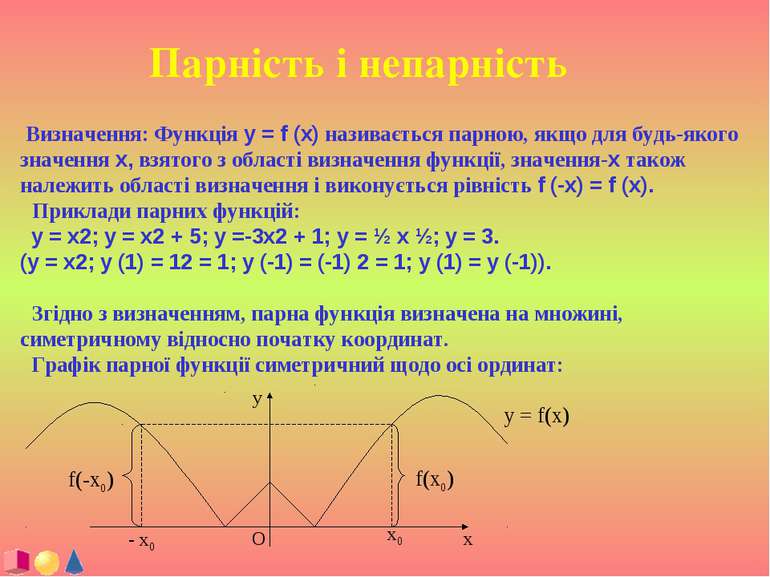
Парність і непарність Визначення: Функція y = f (x) називається парною, якщо для будь-якого значення x, взятого з області визначення функції, значення-x також належить області визначення і виконується рівність f (-x) = f (x).   Приклади парних функцій:   y = x2; y = x2 + 5; y =-3x2 + 1; y = ½ x ½; y = 3. (y = x2; y (1) = 12 = 1; y (-1) = (-1) 2 = 1; y (1) = y (-1)).   Згідно з визначенням, парна функція визначена на множині, симетричному відносно початку координат.   Графік парної функції симетричний щодо осі ординат: y x O x0 - x0

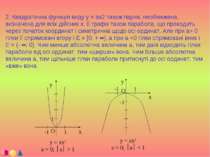
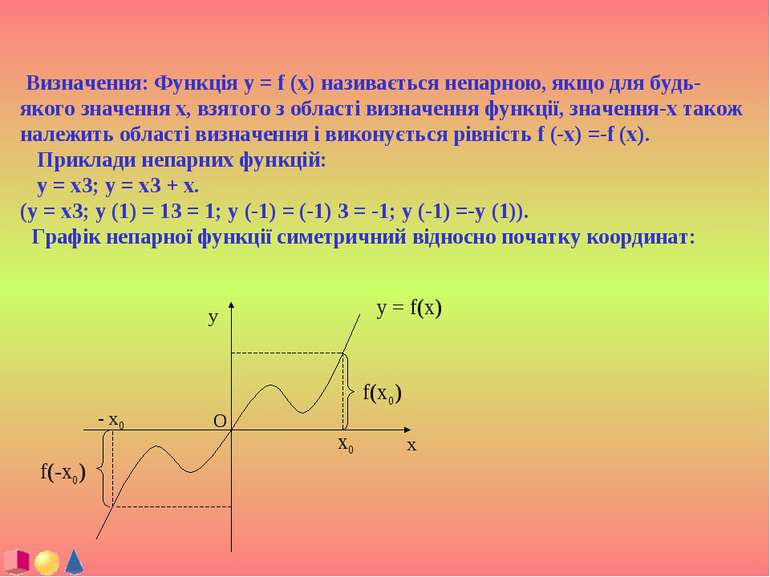
Визначення: Функція y = f (x) називається непарною, якщо для будь-якого значення x, взятого з області визначення функції, значення-x також належить області визначення і виконується рівність f (-x) =-f (x).    Приклади непарних функцій:    y = x3; y = x3 + x. (y = x3; y (1) = 13 = 1; y (-1) = (-1) 3 = -1; y (-1) =-y (1)).   Графік непарної функції симетричний відносно початку координат: f(-x0) O y = f(x)

При побудові графіків парній і непарній функції досить побудувати тільки праву гілку графіка для позитивних значень аргументу. Ліва галузь добудовується симетрично відносно початку координат для непарної функції і відносно осі ординат для парної функції.   Твір двох парних або двох непарних функцій являє собою парну функцію, а твір парній і непарній функцій - непарну функцію.   Звичайно, більшість функцій не є ні парними, ні непарними.   приклад: y = x3 + x2 y(-1) = (-1)3 + (-1)2 = -1 + 1 = 0 y(1) = (1)3 + (1)2 = 1 + 1 = 2

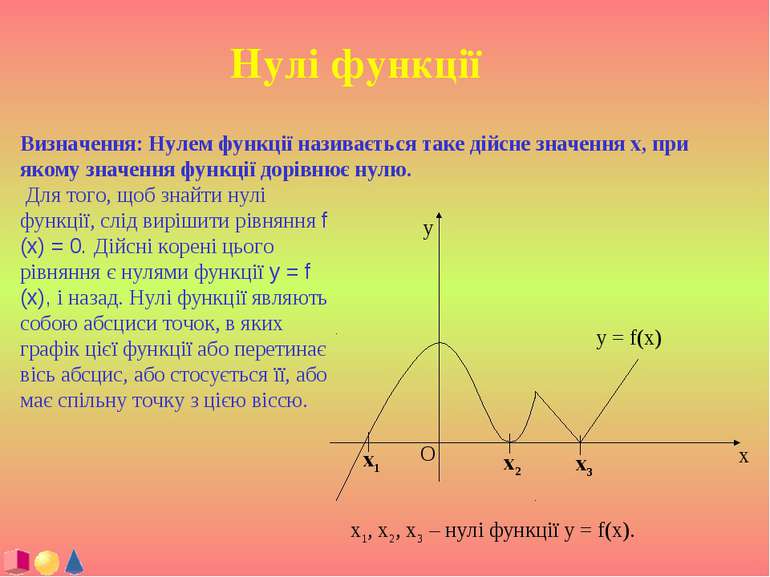
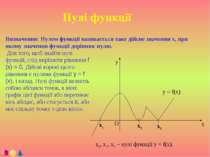
Нулі функції Визначення: Нулем функції називається таке дійсне значення x, при якому значення функції дорівнює нулю. Для того, щоб знайти нулі функції, слід вирішити рівняння f (x) = 0. Дійсні корені цього рівняння є нулями функції y = f (x), і назад. Нулі функції являють собою абсциси точок, в яких графік цієї функції або перетинає вісь абсцис, або стосується її, або має спільну точку з цією віссю. х1, х2, х3 – нулі функції у = f(x).

Екстремуми функції. Найбільше і найменше значення функції Точка x0 називається точкою максимуму (точкою мінімуму) для функції f (x), якщо значення в цій точці більше (менше), ніж значення функції в найближчих сусідніх точках.   для позначення максимуму і мінімуму існує загальний термін «екстремум» (від латинського «крайній»).

Визначення 1. Нехай функція y = f (x) визначена на відрізку [a; b]. Кажуть, що функція має максимум в точці x0, [a; b], якщо існує околиця точки x0, цілком міститься в [a; b] і така, що для будь-якого x, що належить цій околиці, виконується нерівність f (x)

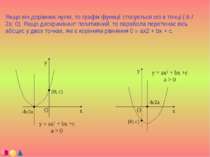
Визначення 2 . Нехай функція y = f ( x ) визначена на відрізку [ a ; b ] . Кажуть , що функція має мінімум в точці x0, [ a ; b ] , якщо існує околиця точки x0 , цілком міститься в [ a ; b ] і така , що для будь-якого x , що належить цій околиці , виконується нерівність f ( x ) > f ( x0) .  Максимуми і мінімуми функції не є обов'язково найбільшими і найменшими значеннями цієї функції у всій області визначення. Наприклад , функція y = f ( x ) визначена на відрізку [ a ; b ] , має чотири екстремуму : два мінімуму ( x = C1 і x = C3) і два максимуму ( x = C2 і x = C4) . Разом з тим , функція досягає найбільшого значення при x = a та найменшого при x = b . Ознака максимуму функції: Якщо функція неперервна в точці x0 і її похідна , переходячи через неї , змінює знак з плюса на мінус ,  то x0 є точка максимуму . Ознака мінімуму функції : Якщо функція неперервна в точці x0 і її похідна , переходячи через неї ,  змінює знак з мінуса на плюс , то x0 є точка мінімуму .

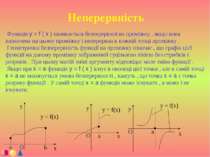
Неперервність Функція y = f ( x ) називається безперервної на проміжку , якщо вона визначена на цьому проміжку і неперервна в кожній точці проміжку .  Геометрична безперервність функції на проміжку означає , що графік цієї функції на даному проміжку зображений суцільною лінією без стрибків і розривів . При цьому малій зміні аргументу відповідає мале зміна функції .  Якщо при x = a функція y = f ( x ) існує в околиці цієї точки , але в самій точці x = a не виконується умова безперервності , кажуть , що точка x = a є точка розриву функції . У самій точці x = a функція може існувати , а може і не існувати.

елементарні функції лінійна квадратична степенева

Лінійна функція Визначення: Функція виду y = kx + b, де k і b деякі числа, називається лінійною функцією.   1. Якщо k = 0, тоді y = b.   Ця функція визначена на множині R і для кожного X приймає одне і те ж значення, рівне b.   Графіком є пряма, паралельна осі Оx і віддалена від неї на ½ b ½ одиниць вгору, якщо b> 0, і вниз, якщо b

2. Якщо b = 0, то y = kx.   Лінійна функція виду y = kx називається прямою пропорційністю. Вона визначена на безлічі R. Функція є монотонно зростаючою, якщо k> 0, і монотонно спадною, якщо k 0 точки графіка належать I і III координатних чвертях. При k

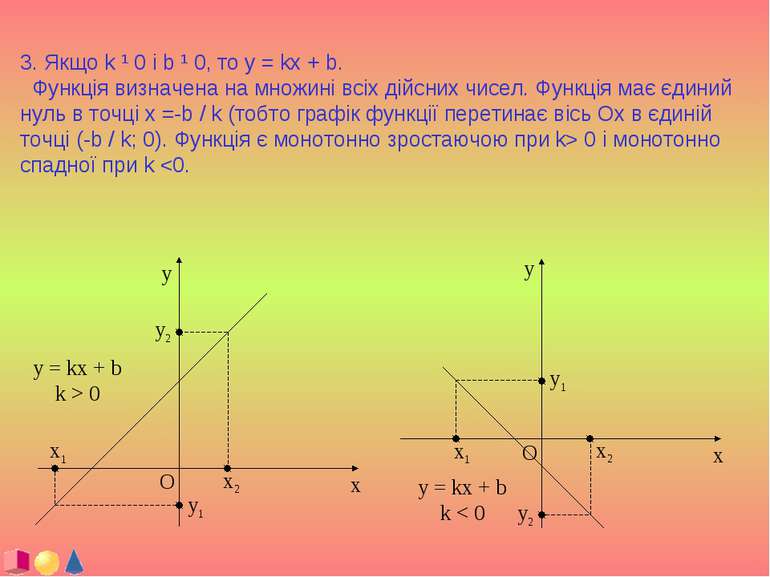
3. Якщо k ¹ 0 і b ¹ 0, то y = kx + b.   Функція визначена на множині всіх дійсних чисел. Функція має єдиний нуль в точці x =-b / k (тобто графік функції перетинає вісь Ох в єдиній точці (-b / k; 0). Функція є монотонно зростаючою при k> 0 і монотонно спадної при k

Коефіцієнти k і b в рівнянні лінійної функції y = kx + b, мають наочне геометричне тлумачення. Значення коефіцієнта b визначає відрізок, що відсікається графіком лінійної функції на осі ординат, а коефіцієнт k визначає тангенс кута a, утвореного віссю абсцис і прямої; кут відраховується від позитивного напрямку осі абсцис. Якщо k> 0, то освічений кут гострий, якщо k

Квадратична функція Визначення: Функція виду y = ax2 + bx + c, де a, b, c - деякі числа, a ¹ 0, називається квадратичною.   1. Функція виду y = x2 - найпростіша квадратична функція. Це парна функція, у якої D = (- ∞; + ∞), а E = [0; + ∞). При x> 0 вона зростаюча, а при x

2. Квадратична функція виду y = ax2 також парна, необмежена, визначена для всіх дійсних x. Її графік також парабола, що проходить через початок координат і симетрична щодо осі ординат. Але при a> 0 гілки її спрямовані вгору і E = [0; + ∞), а при a

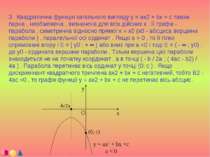
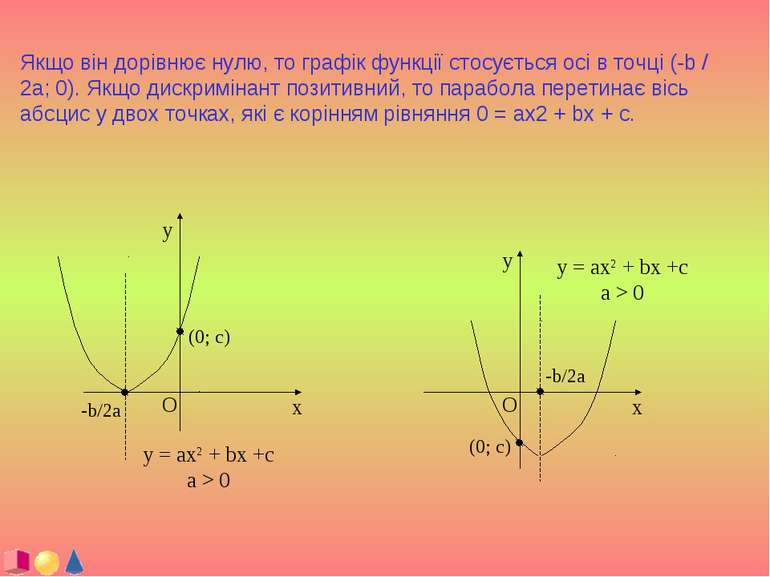
3 . Квадратична функція загального вигляду y = ax2 + bx + c також парна , необмежена , визначена для всіх дійсних x . Її графік - парабола , симетрична відносно прямої x = x0 (x0 - абсциса вершини параболи ) , паралельної осі ординат . Якщо a > 0 , то її гілки спрямовані вгору і E = [ y0 ; + ∞ ) або вниз при a

Якщо він дорівнює нулю, то графік функції стосується осі в точці (-b / 2a; 0). Якщо дискримінант позитивний, то парабола перетинає вісь абсцис у двох точках, які є корінням рівняння 0 = ax2 + bx + c.

Степенева функція Визначення: Функція , задана формулою y = xn , називається статечної .  1 . При n , рівному 1 ; 2 ; -1 , маємо відповідно функції y = x , y = x2 ; y = -1 / x , вже розглянуті раніше .  2 . Якщо n - число ціле і парне , то функція y = xn - парна ; при непарному n вона непарна . При позитивних n ця функція визначена для всіх дійсних значень аргументу x , при негативних n вона визначена для всіх x , крім x = 0.  При будь-якому n ¹ 0 статечна функція необмежена , графік кожній з них проходить через точку ( 1 ; 1).  Якщо n - число ірраціональне , то функція y = xn визначена тільки для позитивних значень аргументу x або для невід'ємних x , якщо n > 0.