Презентація на тему:
Функції, їхні властивості та графіки

Мельниківський НВК Чорнобаївський район Черкаська область Функції, їхні властивості та графіки (10 клас за новою програмою 12-річної школи) Вчитель математики Холощенко Г. Д. 2009 р.

Актуалізація опорних знань учнів по темах “Квадратні корені і дійсні числа”, “Функції і графіки”, з алгебри 7-9 класів дає можливість підготувати учнів до сприйняття теми “Функції, їх властивості та графіки” на уроках алгебри і початків аналізу в 10 класі. Актуалізувати ті елементи їхнього досвіду та уявлення, які будуть опорними при вивченні нового матеріалу можна у ході фронтальної бесіди, розв’язування усних вправ, математичного диктанту, виконання тестових завдань, вправ за готовими рисунками, самостійних робіт, бліцопитування “Встановіть відповідність між…”, колективного розв’язування задач.

Тема уроку. Дійсні числа 1. Фронтальна бесіда 1) Які числа називаються натуральними? 2) Які числа називаються цілими? 3) Які числа називаються раціональними? 4) Які числа називаються ірраціональними? 5) Які числа називаються дійсними? Бліцопитування. 2. Встановіть відповідність між числами і множинами чисел. № Числа 1 1; 2; 3; 4;… 2 …,-3, -2, -1; 0; 12; 3;… 3 ; ; 7,1; 5,6(3); 15;… 4 4 ; ; ;… 5 5 ; 5,6(3); 2112; ; ;… Множини Z цілі Q раціональні N натуральні R дійсні I ірраціональні Z Q N R I 1 2 3 4 5

Тема. Дійсні числа та обчислення. Виконання тестових завдань Варіант 1 Варіант 2 1. Округліть число 0,0278 0,0382 з точністю до тисячних А) 0,028; Б) 0,027; В) 0,02; Г) 0,03 А) 0,03; Б) 0,04; В) 0,038; Г) 0,039 2. Обчисліть значення виразу (-1,8+0,4):0,01 (-2,6+0,5):(-0,01) А) -140; Б) -14; В) -220; Г) -22 А) 310; Б) 31; В) 210; Г) 21 3. Обчисліть значення виразу А) 14; Б) 28; В) 98; Г) 49 А) 15; Б) 75; В) 45; Г) 25 4. Яке з наведених значень хибне А) - ціле число; Б) - натуральне число; В) - раціональне число; Г) - дійсне число А) - дійсне число; Б) - раціональне число; В) - ціле число; Г) - натуральне число 5. Обчисліть значення виразу А) ; Б) ; В) ; Г) А) ; Б) ; В) ; Г)

Тема. Відсотки 1. Фронтальне опитування. 1) Яке значення відсотку від даного числа? 2) Як знайти число за його відсотком? 3) Як знайти відсоткове відношення двох чисел? 2. Виконання тестових завдань. Варіант 1 Варіант 2 1. Запишіть у відсотках 0,76 А) 7,6%; Б) 76%; В) 0,076%; Г) 760% 0,98 А) 98%; Б) 9,8%; В) 0,0098%; Г) 980% 2. Запишіть у вигляді десяткового дробу 166% А) 0,166; Б) 16,6; В) 1,66; Г) 0,0166 134% А) 0,134; Б) 13,4; В) 1,34; Г) 0,0134 3. Знайти 25% від 180 3. Знайти 27% від 200 А) 45; Б) 125; В) 72; Г) 155 А) 54; Б) 5,4; В) 13,5; Г) 540 4. Знайти число, 24% якого дорівнює 48 4. Знайти число, 15% якого дорівнює 30 А) 20; Б) 50; В) 72; Г) 200 А) 20; Б) 50; В) 200; Г) 4,5 5. Скільки відсотків від 180 становить число 50 5. Скільки відсотків від 120 становить число 30 А) 100%; Б) %; В) 30%; Г) 35% А) 4%; Б) 25%; В) 75%; Г) 40% 6. У скільки разів зменшиться число, якщо воно зменшиться на 20% 6. У скільки разів збільшиться число, якщо воно збільшиться на 65% А) в 0,8 раза; Б) в 1,2 раза; В) в 8 разів; Г) в 1,25 раза А) в 0,65 раза; Б) в 1,35 рази; В) в 165 разів; Г) в 1,65 раза

Тема. Відсотки Колективне розв’язування задач. 1. Руда містить 8% міді. Скільки тонн міді міститься в 250 т. цієї руди? 2. Сплав містить 14% цинку. Скільки кілограмів сплаву треба взяти, щоб він містив 5,6 кг. цинку? 3. Поклавши до банку 900 грн., через рік клієнт отримав відсоток, що становив 108 грн. Скільки відсотків річних сплачує цей банк? 4. Ціна товару підвищилась з 600 грн. до 624, грн.. На скільки відсотків відбулось підвищення?

Тема. Числові функції. Виконання усних вправ. 1) Функцію задано формулою Знайдіть . 2) При яких значеннях аргументна значення функції перетворюється на нуль. 3) Функцію задано формулою . Порівняйте: а) і ; б) і .

Тема уроку. Область визначення і множина значень. Способи задання функцій. Колективне розв’язування задач. 1. Знайти область визначення функції а) ; б) ; в) ; г) . 2. Знайти область значень функції а) ; б) ; в) ; г) . 3. Функція задана за допомогою таблиці. Задати функцію за допомогою формули. 4. Побудувати графік функції . х -3 -2 -1 0 1 2 3 у -27 -8 -1 0 1 8 27

Тема. Графік функції Математичний диктант Варіант 1 Варіант 2 Вставте пропущені місця в тексті 1. Для, того щоб побудувати графік функції необхідно графік функції … перенести на … одиниць… 2. Для, того щоб побудувати графік функції необхідно графік функції … перенести на … одиниць… 3. Для, того щоб побудувати графік функції необхідно графік функції … перенести на … одиниць… 4. Якщо графік функції перенести на 12 одиниць ліворуч на 20 одиниць праворуч то дістанемо графік функції…

Тема. Графік функції. Монотонність, парність і непарність функцій Виконання вправ за готовими рисунками. Сформулювати властивості зображених на рисунку функцій за такою схемою: 1. Область визначення; 2. Область значень; 3. Нулі функції; 4. Проміжки знакосталості; 5. Парність, непарність; 6. Проміжки зростання та спадання; 7. Найбільше та найменше значення.

Тема. Неперервність функції Самостійна робота з подальшою перевіркою та обговорення Варіант 1 Варіант 2 1. Знайти область визначення функції а) ; б) ; в) ; г) а) ; б) ; в) ; г) 2. Побудувати графік функції

Тема. Корінь n-го степеня Математичний диктант Варіант 1 Варіант 2 1. Покажіть, що: 8 5 Квадратний корінь з 64 25 Чи існують інші квадратні корені з числа 64 25 2. Покажіть, що: а) 6,3; б) 0,99 квадратний корінь з числа а) 5,4; б) 0,86 квадратний корінь з числа а) 39,69; б) 0,9801 а) 29,16; б) 0,7396 3. Знайдіть від’ємні значення коренів з чисел 256 289

Тема. Арифметичний корінь n-го степеня Встановіть відповідність між виразами і їх значеннями 1 2 3 4 5 6 А 110 Б 0,01 В 0,09 Г 1,1 Д 11 Е 0,11 А Б В Г Д Е 1 2 3 4 5 6

Тема. Властивості арифметичного кореня n-го степеня Самостійна робота з взаємоперевіркою Варіант 1 Варіант 2 1. Обчисліть значення виразу а) ; б) ; в) ; г) ; д) ; е) а) ; б) ; в) ; г) ; д) ; е) 2. Спростіть вираз , якщо х

Тема. Найпростіші перетворення коренів Виконання тестових завдань Варіант 1 Варіант 2 1. Чому дорівнює значення виразу а) 15; б) 45; в) 75; г) 125 а) 16; б) 18; в) 12; г) 6 2. Обчисліть значення виразу а) 49; б) 96; в) 10; г) 7 а) 4; б) 16; в) 75; г) 8 3. Спростіть вираз а) ; б) ; в) ; г) а) ; б) ; в) ; г) 4. Обчисліть а) 37; б) 27; в) 7; г) 57 а) 25; б) 19; в) 31; г) 37 5. Звільніться від ірраціональності в знаменнику дробу а) ; б) ; в) ; г) а) ; б) ; в) ; г)

Тема. Найпростіші перетворення коренів Самостійна робота з самоперевіркою за готовими відповідями. Варіант 1 Варіант 2 1. Впишіть множник під знак кореня а) ; б) ; в) ; г) , m

Тема. Найпростіші перетворення коренів Самостійна робота з самоперевіркою за готовими відповідями. Відповіді: Варіант 1 Варіант 2 1. Впишіть множник під знак кореня а) ; б) ; в) ; г) , m

Тема. Спрощення виразів, що містять корені Виконання тестових завдань Варіант 1 Варіант 2 1. Спростіть вираз а) ; б) ; в) ; г) а) ; б) ; в) ; г) 2. Виконайте множення а) ; б) ; в) ; г) а) ; б) ; в) ; г) 3. Спростіть вираз а) 6; б) 8; в) 48; г) 50 а) 120; б) 122; в) 10; г) 12 4. Знайдіть значення виразу а) 18; б) 54; в) 36; г) 72 а) 20; б) 80; в) 40; г) 100 5. Скоротіть дріб а) ; б) ; в) ; г) а) ; б) ; в) ; г)

Тема. Степені з раціональними показниками, їхні властивості Фронтальна бесіда. 1. Як помножити степені з однією основою? 2. Як виконати ділення степенів з однією основою? Навести приклад. 3. Як навести степінь до степеня? Навести приклад. 4. Чому дорівнює n-ий степінь добутку? Навести приклад. 5. Чому дорівнює ? 6. Чому дорівнює ?

Тема. Властивості степеня з раціональним показником Виконання тестових завдань Варіант 1 Варіант 2 1. Подайте вираз у вигляді степеня з основою а) ; б) ; в) ; г) у вигляді степеня з основою а) ; б) ; в) ; г) 2. Виконайте множення а) ; б) ; в) ; г) а) ; б) ; в) ; г) 3. Виконайте піднесення до степеня: а) ; б) ; в) ; г) а) ; б) ; в) ; г) 4. Обчисліть значення виразу а) 1; б) -1; в) 5; г) -5 а) -2; б) 2; в) -1; г) 1

Тема. Степенева функція Фронтальна бесіда 1. Яка область визначення функції ? 2. Яка область значень функції ? 3. Яка область визначення функції ? 4. Яка область значень функції ? 5. Що є графіком функції ? Побудувати графік. 6. Що є графіком функції ? Побудувати графік. 7. Як розміщений графік функції відносно осі у? 8. Які властивості має функція ? 9. Як розміщений графік функції відповідно початку координат? 10. Які властивості має функція ?

Тема. Властивості степеневої функції та графіки Колективне виконання вправ. 1. Як розміщено графік функції , якщо n – непарне? 2. Накреслити ескіз графіка функції . 3. Накреслити ескізи графіків функції і . 4. Чим відрізняються між собою графіки функції і . Побудувати ескізи. 5. Чи знайдеться таке натуральне значення р, при якому графік функції проходить через точку: а) А(1;1); б) В(;81); в) С(-5;6,25); г) Д(-7;343)?

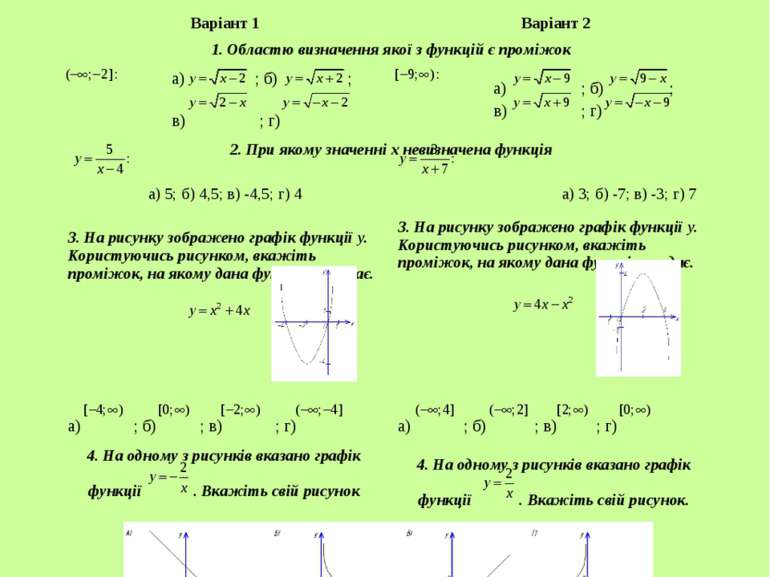
Тема. Графіки степеневої функції Виконання тестових завдань Варіант 1 Варіант 2 1. Областю визначення якої з функцій є проміжок а) ; б) ; в) ; г) а) ; б) ; в) ; г) 2. При якому значенні х невизначена функція а) 5; б) 4,5; в) -4,5; г) 4 а) 3; б) -7; в) -3; г) 7 3. На рисунку зображено графік функції у. Користуючись рисунком, вкажіть проміжок, на якому дана функція зростає. 3. На рисунку зображено графік функції у. Користуючись рисунком, вкажіть проміжок, на якому дана функція спадає. а) ; б) ; в) ; г) а) ; б) ; в) ; г) 4. На одному з рисунків вказано графік функції . Вкажіть свій рисунок 4. На одному з рисунків вказано графік функції . Вкажіть свій рисунок.

Література 1. Г. Янченко, В. Кравчук. Алгебра, 7 клас, 2007 р. 2. Г. Янченко. Алгебра, 8 клас, 2008 р. 3. Г. Янченко, В. Кравчук, М. Підручна. Алгебра, 9 клас, 2009 р. 4. Математика 5-12 класи. Програма для загальноосвітніх навчальних закладів. Київ, 2005 р.