Презентація на тему:
Функція. Графік функції

Функція. Графік функції. 7 клас.

Автомобіль рухається по шосе з постійною швидкістю 70 км/год. За час t год. автомобіль проходить шлях S = 70 · t км. Легко обчислити пройдений шлях за будь-який час: Якщо t = 1, то Якщо t = 1,5, то Якщо t = 3, то S = 70 · 1 = 70 S = 70 · 1,5 = 105 S = 70 · 3 = 210 S = 70 · t Незалежна змінна АРГУМЕНТ Залежна змінна ФУНКЦІЯ

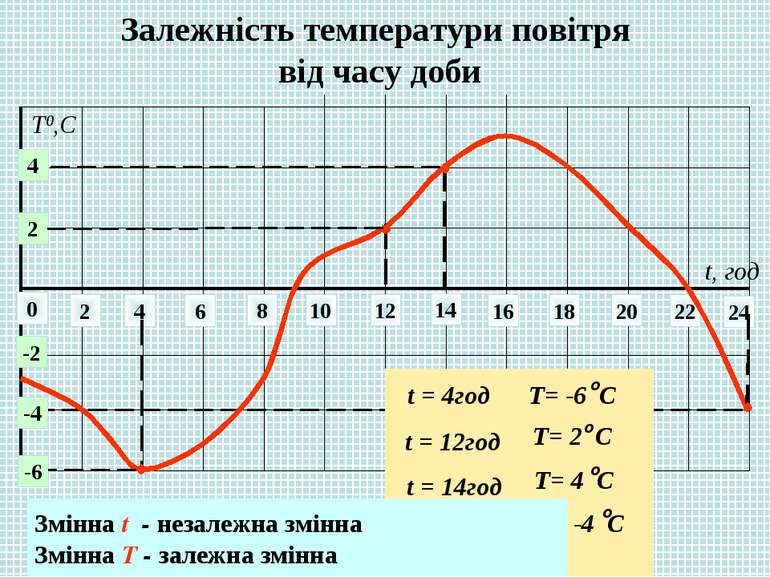
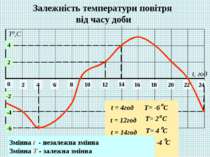
Залежність температури повітря від часу доби 0 2 4 6 8 10 12 14 22 24 16 18 20 t, год 2 4 -2 -6 -4 Т0,С Змінна t - незалежна змінна Змінна T - залежна змінна

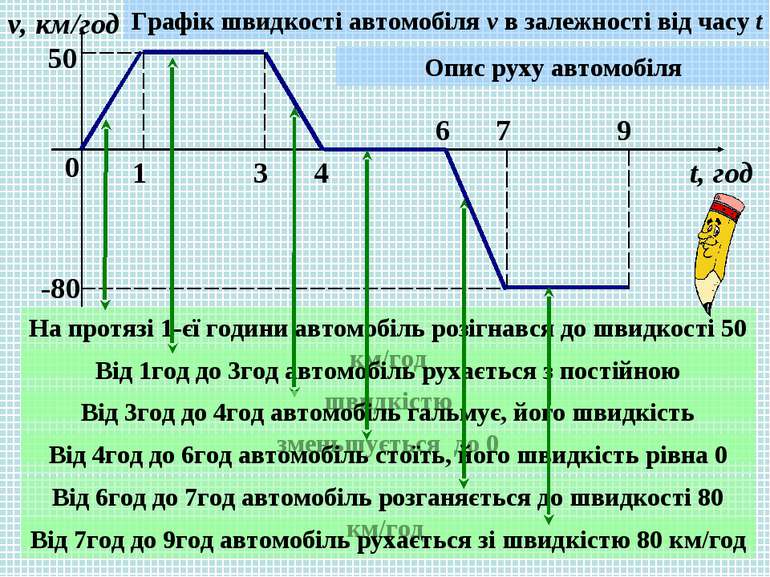
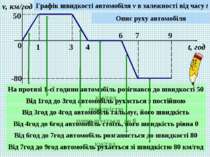
0 1 3 4 6 7 9 v, км/год t, год 50 -80 Графік швидкості автомобіля v в залежності від часу t Опис руху автомобіля На протязі 1-єї години автомобіль розігнався до швидкості 50 км/год Від 1год до 3год автомобіль рухається з постійною швидкістю Від 3год до 4год автомобіль гальмує, його швидкість зменьшується до 0 Від 4год до 6год автомобіль стоїть, його швидкість рівна 0 Від 6год до 7год автомобіль розганяється до швидкості 80 км/год Від 7год до 9год автомобіль рухається зі швидкістю 80 км/год

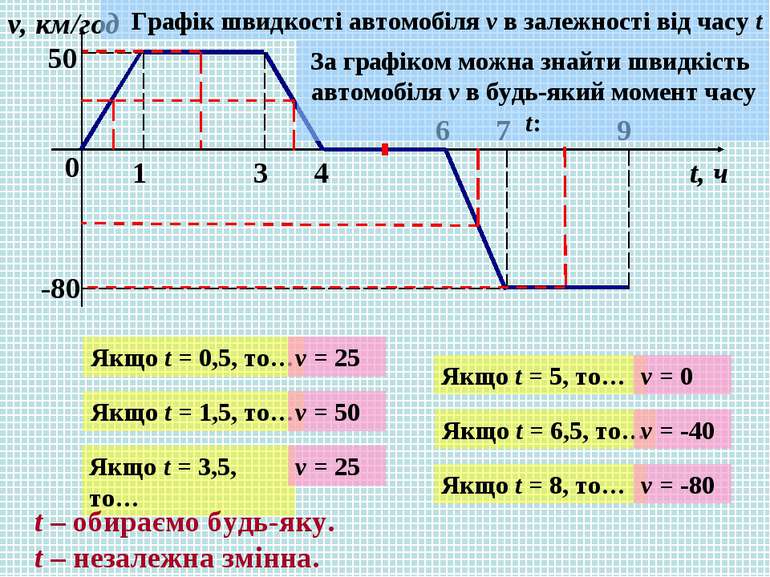
0 1 3 4 6 7 9 v, км/год t, ч 50 -80 Графік швидкості автомобіля v в залежності від часу t За графіком можна знайти швидкість автомобіля v в будь-який момент часу t: Якщо t = 0,5, то… Якщо t = 1,5, то… Якщо t = 3,5, то… Якщо t = 5, то… Якщо t = 6,5, то… Якщо t = 8, то… v = 25 v = 50 v = 25 v = 0 v = -40 v = -80 t – обираємо будь-яку. t – незалежна змінна.

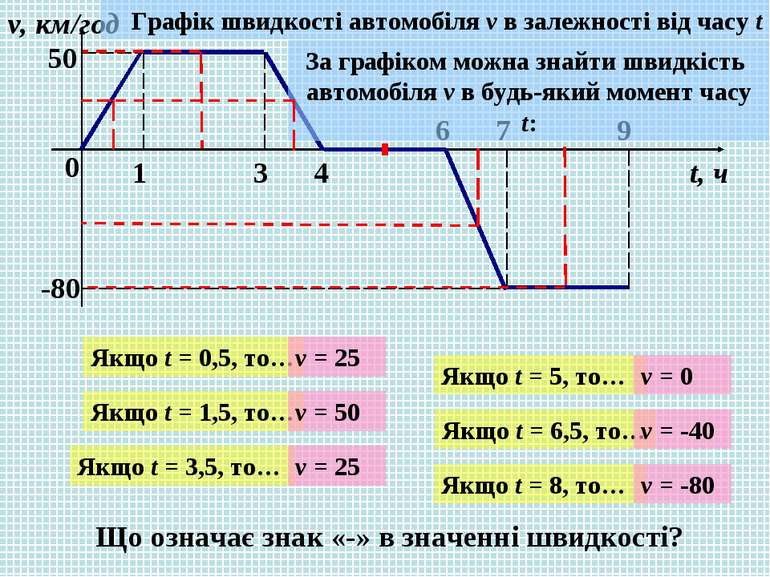
0 1 3 4 6 7 9 v, км/год t, ч 50 -80 Графік швидкості автомобіля v в залежності від часу t За графіком можна знайти швидкість автомобіля v в будь-який момент часу t: Якщо t = 0,5, то… Якщо t = 1,5, то… Якщо t = 3,5, то… Якщо t = 5, то… Якщо t = 6,5, то… Якщо t = 8, то… v = 25 v = 50 v = 25 v = 0 v = -40 v = -80 Що означає знак «-» в значенні швидкості?

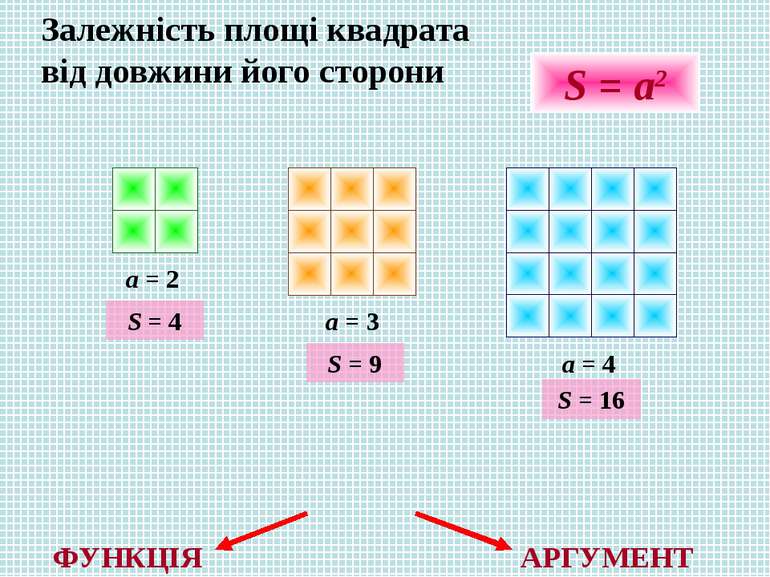
Залежність площі квадрата від довжини його сторони a = 2 a = 3 a = 4 S = a2 S = 4 S = 9 S = 16 ФУНКЦІЯ АРГУМЕНТ

Таблиця квадратів натуральних чисел: 1 4 9 16 25 36 49 64 81 100 Для кожного значення х можна знайти єдине значення у у = х2 АРГУМЕНТ ФУНКЦІЯ х 1 2 3 4 5 у = х2 х 6 7 8 9 10 у = х2

В розглянутих прикладах кожному значенню незалежній змінній відповідає єдине значення залежної змінної. Залежність однієї змінної від іншої називається - функцією.

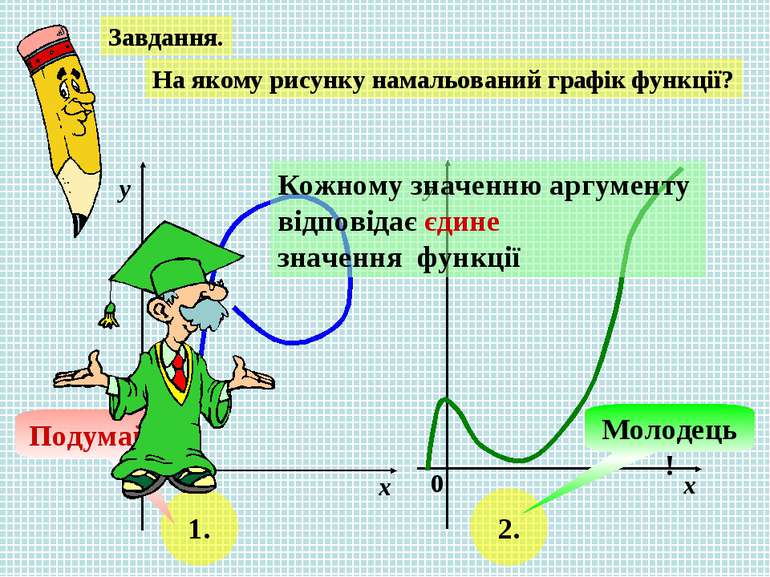
Завдання. На якому рисунку намальований графік функції? х у 0 х у 0 1. 2. Подумай! Молодець! Кожному значенню аргументу відповідає єдине значення функції

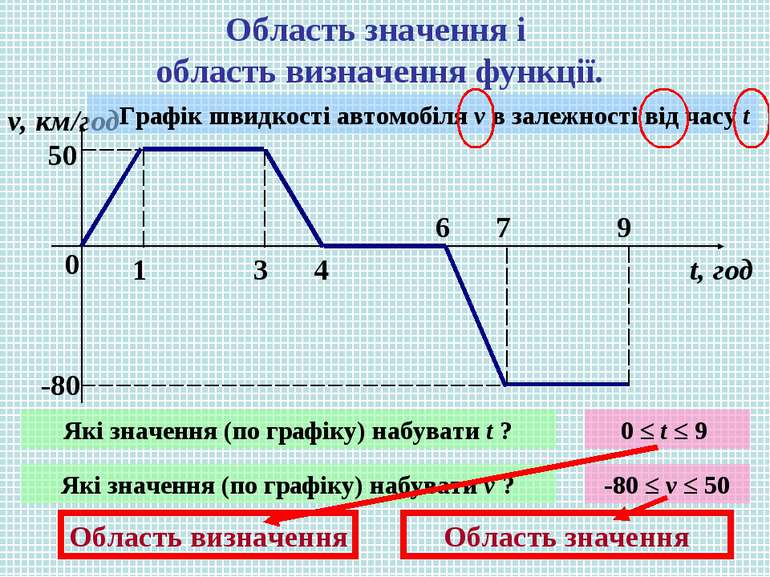
Область значення і область визначення функції. 0 1 3 4 6 7 9 v, км/год t, год 50 -80 Графік швидкості автомобіля v в залежності від часу t Які значення (по графіку) набувати t ? 0 ≤ t ≤ 9 Які значення (по графіку) набувати v ? -80 ≤ v ≤ 50 Область визначення Область значення

Область значення і область визначення функції. Автомобіль рухається по шосе з постійною швидкістю 70 км/год. За час t год. автомобіль проходить шлях S = 70 · t км. Які значення може набувати t ? Які значення може набувати S ? t ≥ 0 S ≥ 0 Всі значення, які набуває незалежна змінна утворюють область визначення функції Значення залежної змінної утворюють область значення функції

Завдання. Об’єм куба залежить від довжини його ребра. Нехай а см – довжина ребра куба, V см3 – його об’єм. Задайте формулою залежність V від а. Знайдіть значення функції V при а = 5; 7,1. Перевірка.(3) а а а V = а3 Якщо а = 5, то V = 53 = 125 Якщо а = 7,1, то V = 357,911

Подання функції за допомогою формули. Формула дозволяє для будь-якого значення аргументу знаходити відповідне значення функції шляхом обчислення. Приклад 1. Знайти значення функції y(x) = x3 + x при х = - 2; х = 5; х = а; х = 3а. 1. у(-2) = (-2)3 + (-2) = -8 – 2 = -10 2. у(5) = 53 + 5 = 125 + 5 = 130 3. у(а) = а3 + а 4. у(3а) = (3а)3 + 3а = 27а3 + 3а

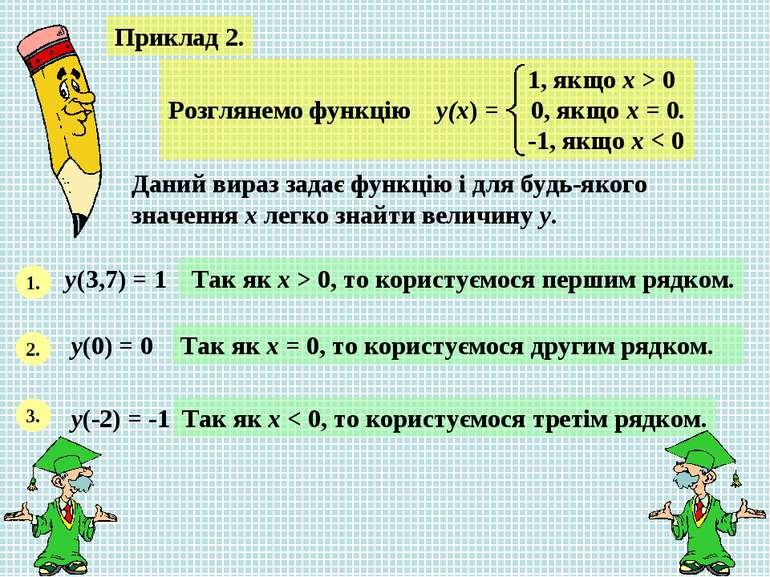
Приклад 2. Даний вираз задає функцію і для будь-якого значення х легко знайти величину у. 1. у(3,7) = 1 Так як х > 0, то користуємося першим рядком. 2. у(0) = 0 Так як х = 0, то користуємося другим рядком. 3. у(-2) = -1 Так як х < 0, то користуємося третім рядком.

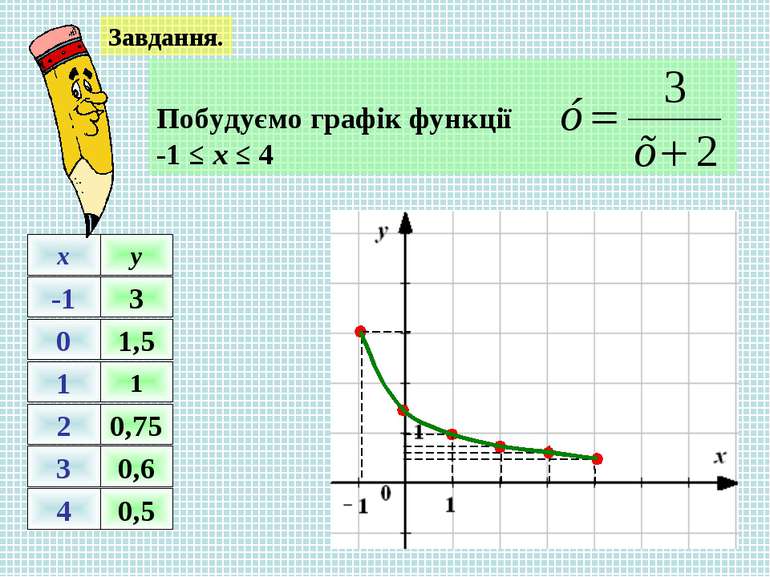
Приклад 3. 1. В цьому прикладі область визначення вказана – всі значення х з проміжку 2 ≤ х ≤ 9 2. В цьому випадку область визначення не вказана. Знайдемо значення аргументу, при яких формула для функції має зміст. Переглянути розв’язок

Завдання. Знайдіть область визначення функції: 1. 2. 3.

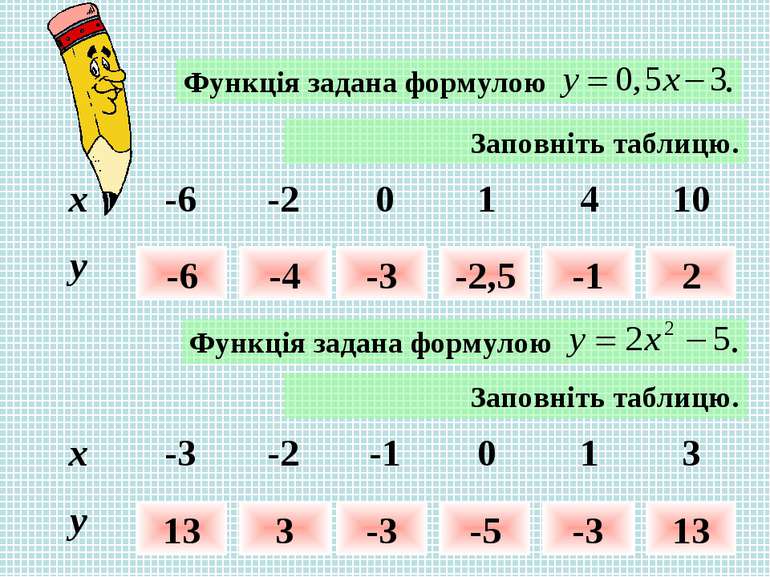
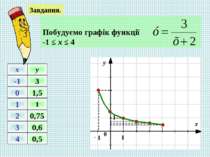
Заповніть таблицю. -6 -4 -3 -2,5 -1 2 Заповніть таблицю. 13 3 -3 -5 -3 13 x -6 -2 0 1 4 10 y x -3 -2 -1 0 1 3 y

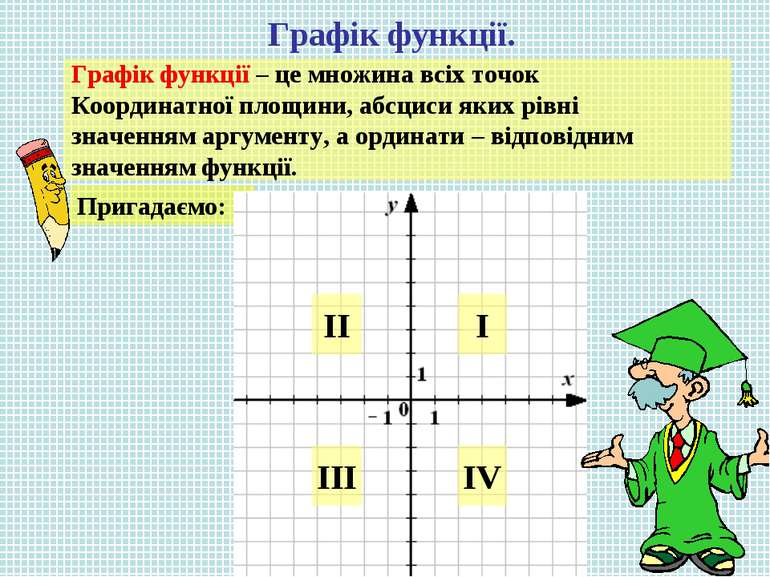
Графік функції. Графік функції – це множина всіх точок Координатної площини, абсциси яких рівні значенням аргументу, а ординати – відповідним значенням функції. Пригадаємо: IV III II I

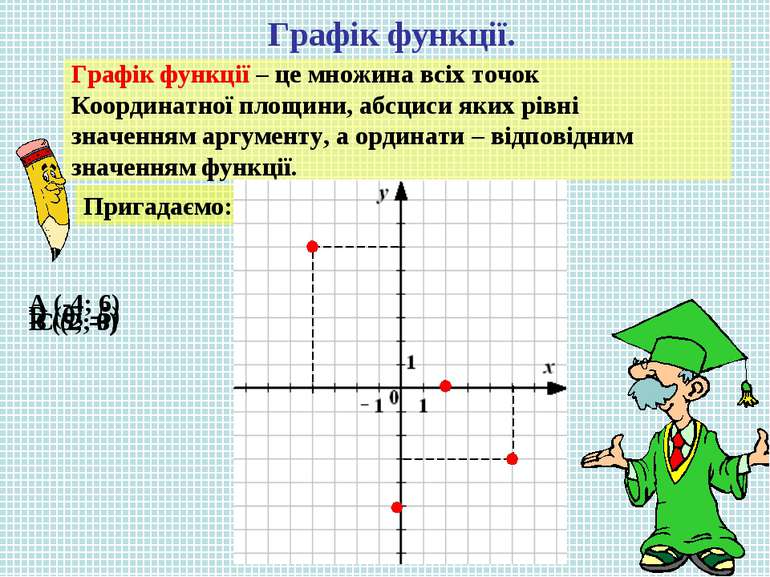
Графік функції. Графік функції – це множина всіх точок Координатної площини, абсциси яких рівні значенням аргументу, а ординати – відповідним значенням функції. Пригадаємо: A (-4; 6) B (5; -3) C (2; 0) D (0; -5)

Завдання. -1 0 1 2 3 4 x y 1 0,75 0,6 0,5 3 1,5

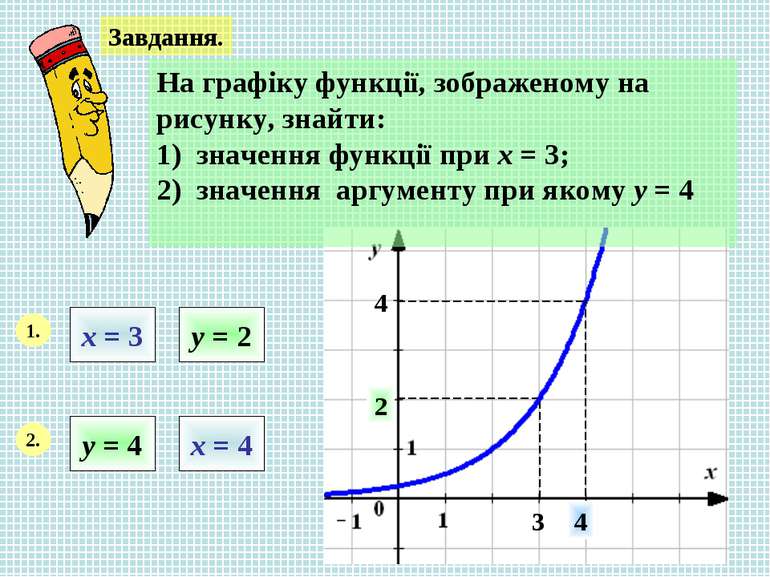
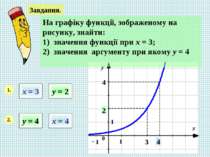
Завдання. На графіку функції, зображеному на рисунку, знайти: 1) значення функції при х = 3; 2) значення аргументу при якому у = 4 1. х = 3 у = 2 3 2 2. у = 4 4 4 х = 4

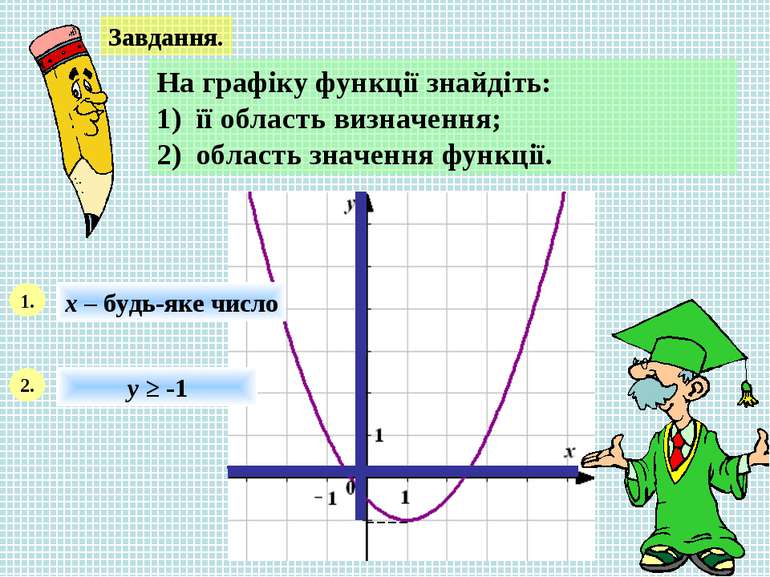
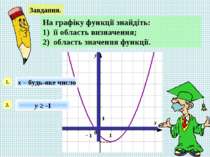
Завдання. На графіку функції знайдіть: 1) її область визначення; 2) область значення функції. 1. х – будь-яке число 2. у ≥ -1

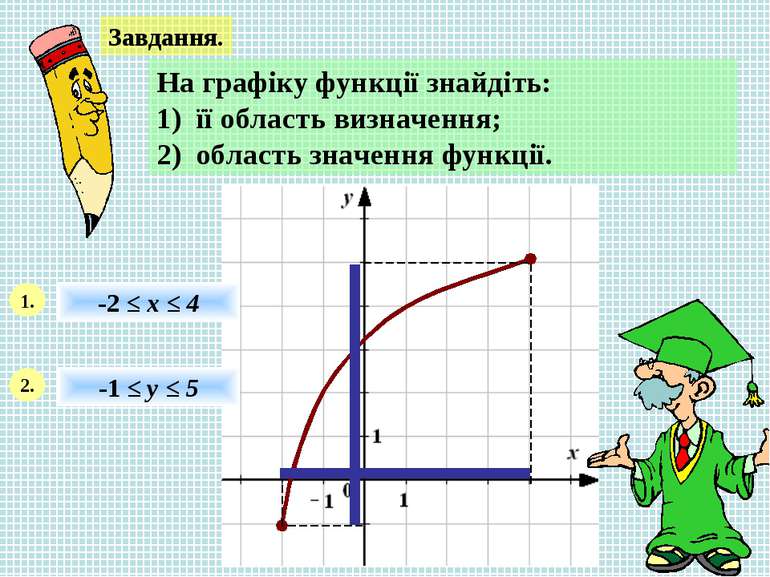
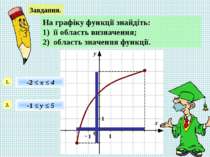
Завдання. На графіку функції знайдіть: 1) її область визначення; 2) область значення функції. 1. 2. -2 ≤ х ≤ 4 -1 ≤ у ≤ 5

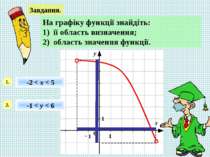
Завдання. На графіку функції знайдіть: 1) її область визначення; 2) область значення функції. 1. 2. -2 < х < 5 -1 < у < 6

Знайдемо значення аргументу при яких формула як функція має зміст. Так, як формула являє собою дріб, то її знаменник не може дорівнювати нулю, тобто , звідси і Отже, область значення даної функції – всі значення х, крім чисел -3 і 1.