Презентація на тему:
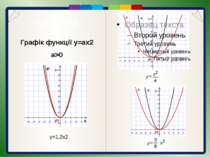
Графік функції y=(x+m)2+n. Графік функції y=ax2

Тема 3 Функція. Квадратична функція Поняття квадратичної функції. Графік функції y=x2+n. Графік функції y=(x+m)2 Графік функції y=(x+m)2+n. Графік функції y=ax2 Графік функції y=a(x+m)2+n Графік функції y=ax2+bx+c Властивості квадратичної функції Найпростіші перетворення графіків функцій Розв’язування вправ. Самостійна робота Розв'язування вправ

Пункт 3.4-3.5. Пригадайте: 1). Що є графіком функції y=(x+m)2? 2). Що є графіком функції y=x2 +n? Графік функції y=(x+m)2+n Графік функції y=ax2

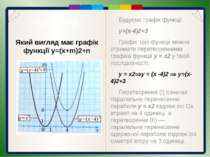
Пункт 3.4-3.5. Будуємо графік функції y=(x+2)2-3 Графік цієї функції можна отримати перетвореннями графіка функції у = х2 у такій послідовності: у = х2 у = (х + 2)2 y=(x+2)2-3 Перетворення (І) означає паралельне перенесення параболи у = х2 вздовж осі Oх вліво на 2 одиниці, а перетворення (ІІ) — паралельне перенесення одержаної параболи вздовж осі симетрії вниз на 3 одиниці. Який вигляд має графік функції y=(x+m)2+n

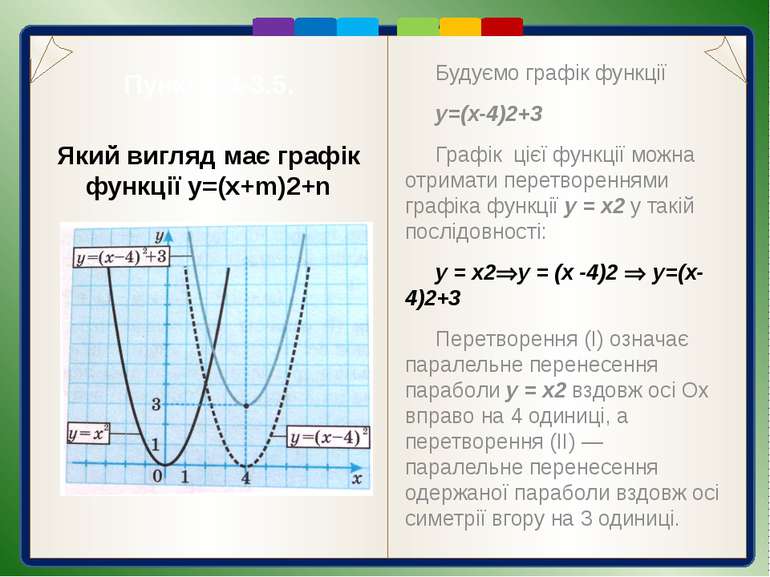
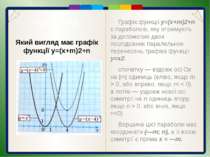
Пункт 3.4-3.5. Будуємо графік функції y=(x-4)2+3 Графік цієї функції можна отримати перетвореннями графіка функції у = х2 у такій послідовності: у = х2 у = (х -4)2 y=(x-4)2+3 Перетворення (І) означає паралельне перенесення параболи у = х2 вздовж осі Oх вправо на 4 одиниці, а перетворення (ІІ) — паралельне перенесення одержаної параболи вздовж осі симетрії вгору на 3 одиниці. Який вигляд має графік функції y=(x+m)2+n

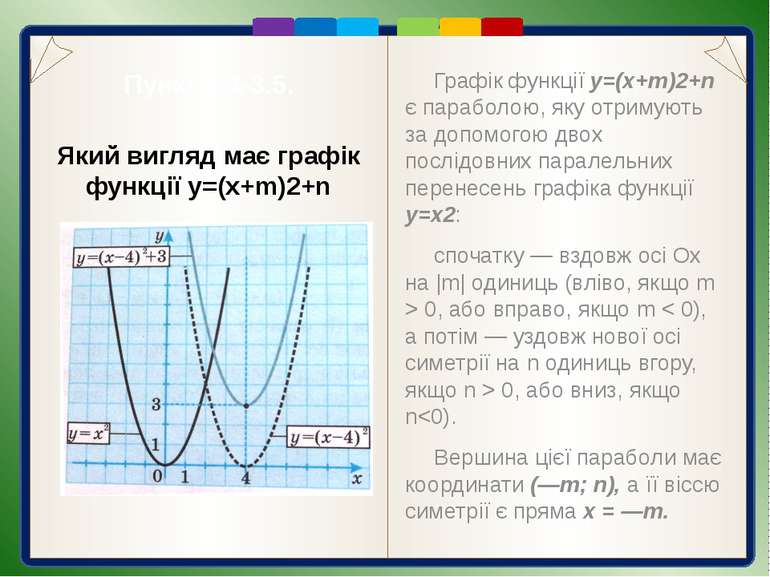
Пункт 3.4-3.5. Графік функції y=(x+m)2+n є параболою, яку отримують за допомогою двох послідовних паралельних перенесень графіка функції у=x2: спочатку — вздовж осі Ох на |m| одиниць (вліво, якщо m > 0, або вправо, якщо m < 0), а потім — уздовж нової осі симетрії на n одиниць вгору, якщо n > 0, або вниз, якщо n

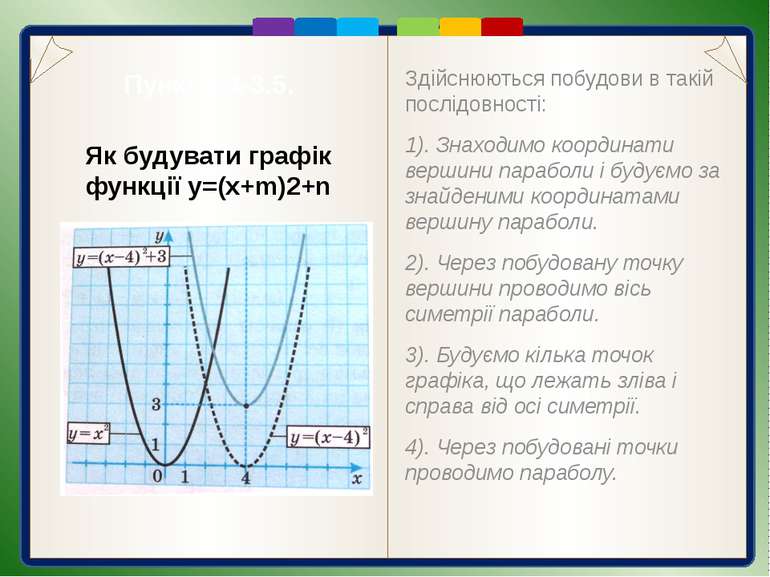
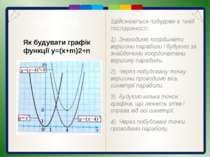
Пункт 3.4-3.5. Здійснюються побудови в такій послідовності: 1). Знаходимо координати вершини параболи і будуємо за знайденими координатами вершину параболи. 2). Через побудовану точку вершини проводимо вісь симетрії параболи. 3). Будуємо кілька точок графіка, що лежать зліва і справа від осі симетрії. 4). Через побудовані точки проводимо параболу. Як будувати графік функції y=(x+m)2+n

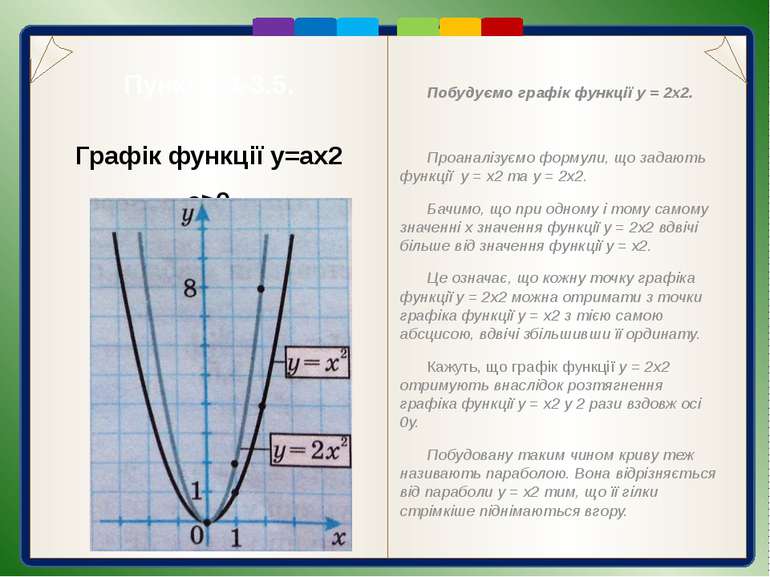
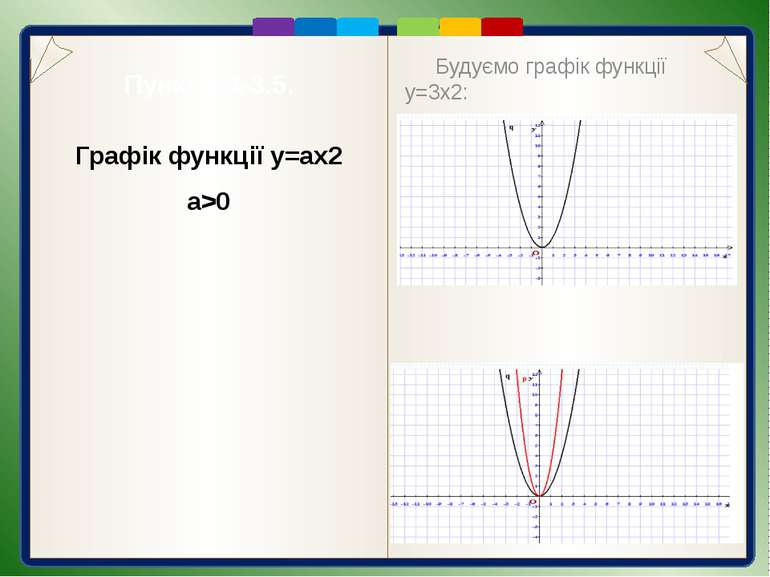
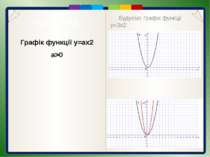
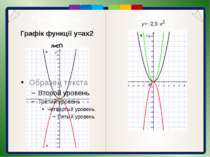
Пункт 3.4-3.5. Графік функції y=ax2 a>0 Побудуємо графік функції у = 2х2. Проаналізуємо формули, що задають функції у = х2 та у = 2х2. Бачимо, що при одному і тому самому значенні х значення функції у = 2х2 вдвічі більше від значення функції у = х2. Це означає, що кожну точку графіка функції у = 2х2 можна отримати з точки графіка функції у = х2 з тією самою абсцисою, вдвічі збільшивши її ординату. Кажуть, що графік функції у = 2х2 отримують внаслідок розтягнення графіка функції у = х2 у 2 рази вздовж осі 0у. Побудовану таким чином криву теж називають параболою. Вона відрізняється від параболи у = х2 тим, що її гілки стрімкіше піднімаються вгору.

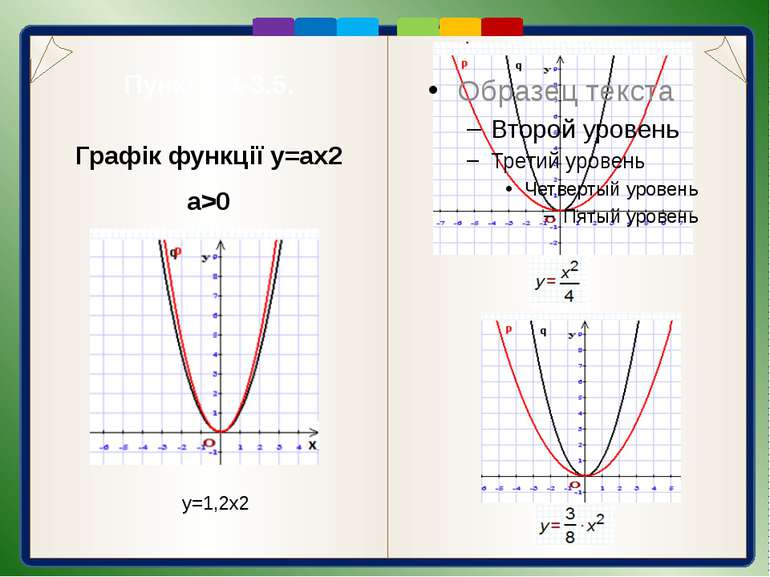
Пункт 3.4-3.5. Будуємо графік функції у=3х2: 1). Будуємо графік функції у=х2 2). Виконаємо розтягнення від осі ОХ параболи у=х2 в 3 рази. Графік функції y=ax2 a>0

Пункт 3.4-3.5. Графік функції y=ax2 a>0 y=1,2x2

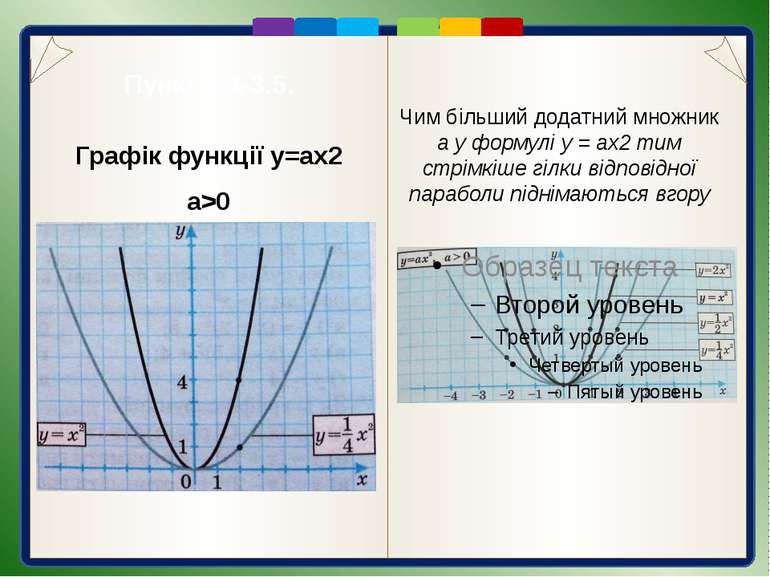
Пункт 3.4-3.5. Графік функції y=ax2 a>0 Чим більший додатний множник а у формулі у = ax2 тим стрімкіше гілки відповідної параболи піднімаються вгору

Пункт 3.4-3.5. Графік функції y=ax2 a

Пункт 3.4-3.5. Графік функції y=ax2 a

Пункт 3.4-3.5. Графік функції y=ax2 a

Пункт 3.4-3.5. Графік функції y=ax2 a

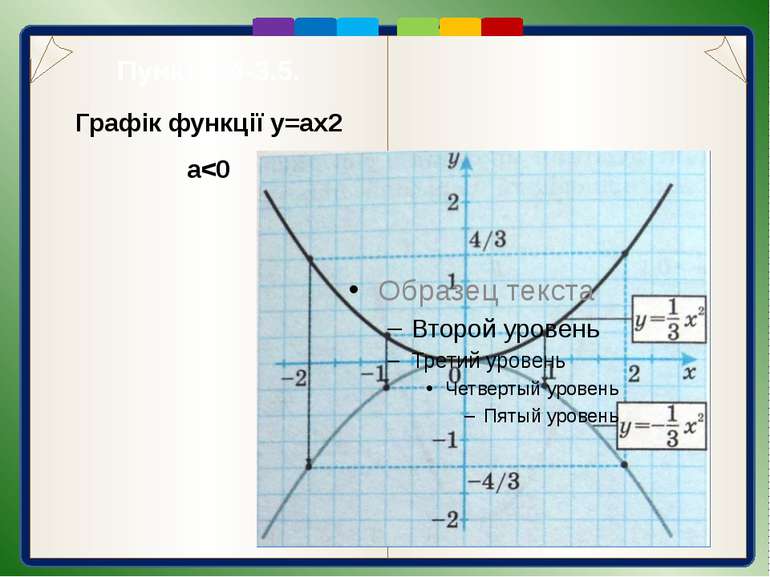
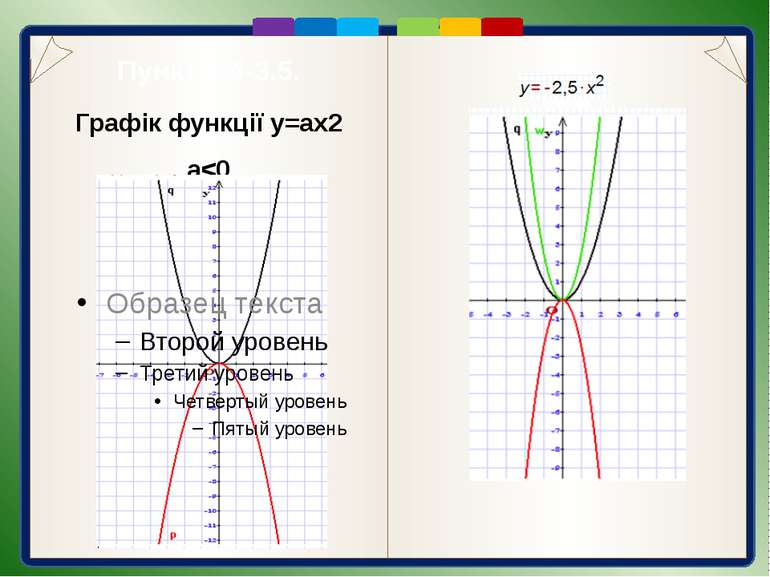
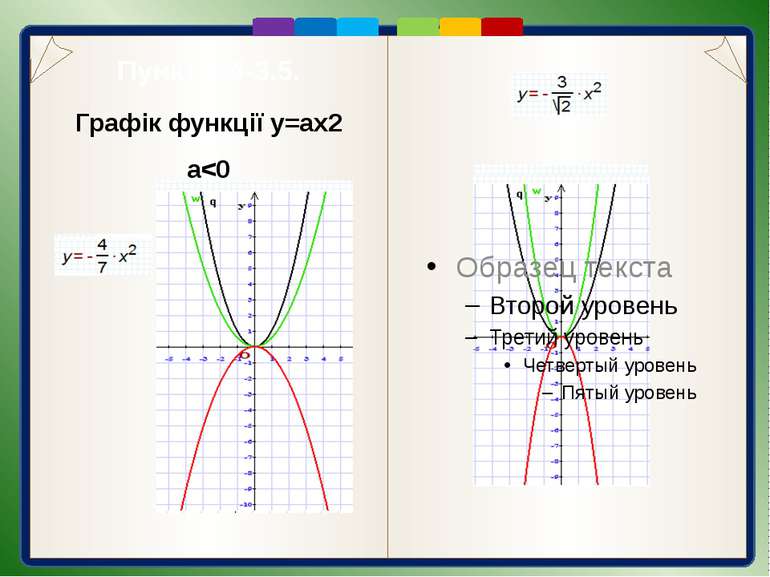
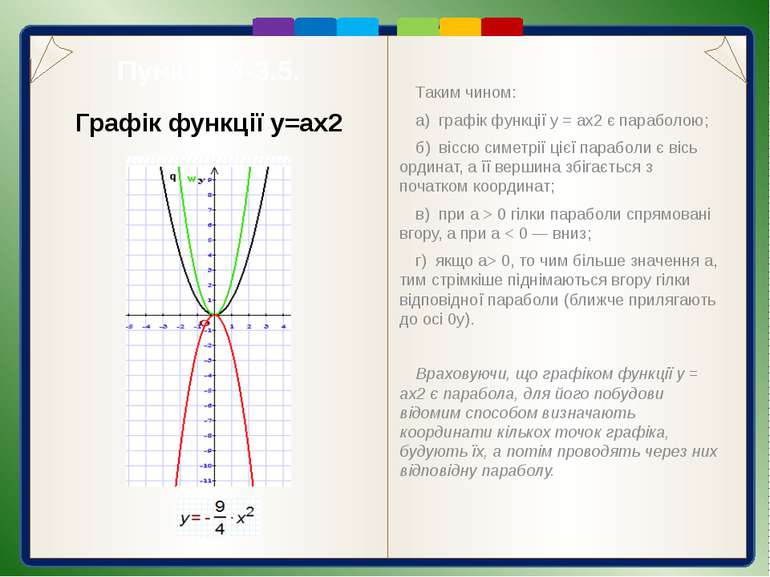
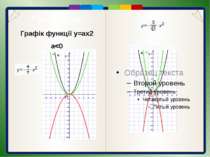
Пункт 3.4-3.5. Графік функції y=ax2 a 0 гілки параболи спрямовані вгору, а при а < 0 — вниз; г) якщо а> 0, то чим більше значення а, тим стрімкіше піднімаються вгору гілки відповідної параболи (ближче прилягають до осі 0у). Враховуючи, що графіком функції у = ах2 є парабола, для його побудови відомим способом визначають координати кількох точок графіка, будують їх, а потім проводять через них відповідну параболу.

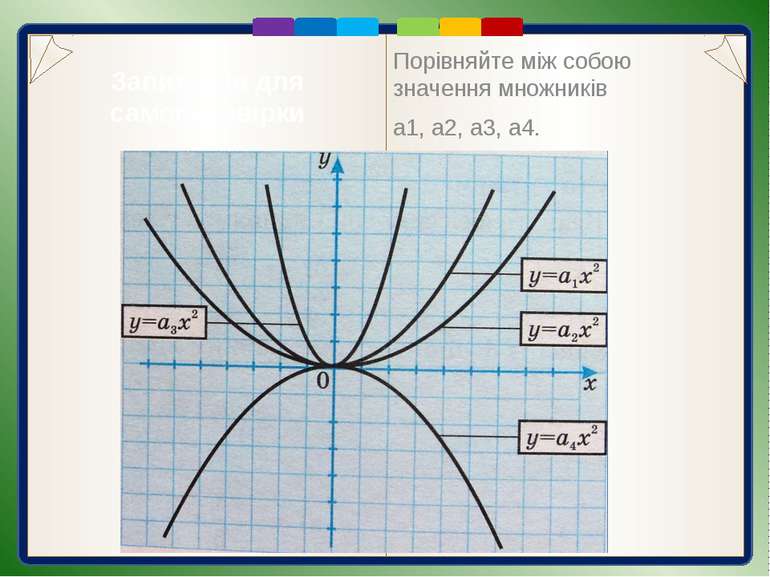
Запитання для самоперевірки Що є графіком функції у = (х + 3,5)2 — 1? 2) Опишіть послідовність побудови цього графіка. 3) Що є графіком функції у=ах2? 4) Як впливає на вигляд графіка функції у=ах2 знак множника а? 5) Через яку точку проходять графіки всіх функцій виду у=ах2?

Запитання для самоперевірки Порівняйте між собою значення множників а1, а2, а3, а4.