Презентація на тему:
Площа бічної та повної поверхонь конуса

Площа бічної та повної поверхонь конуса 11 клас

МЕТА УРОКУ 1. Домогтися засвоєння формул для обчислення площ бічної та повної поверхонь конуса; 2. Сформулювати вміння розв'язувати задачі на обчислення площ бічної та повної поверхонь конуса.

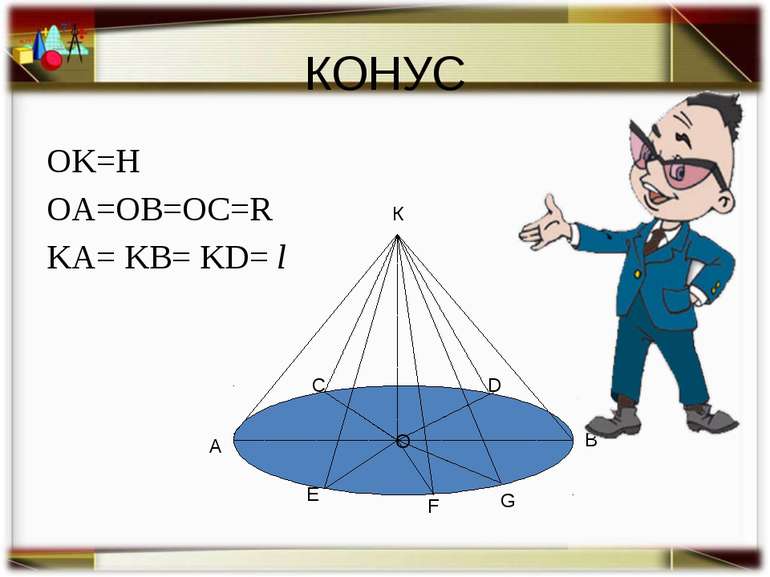
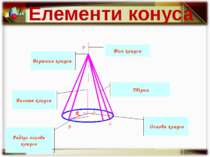
Назва цієї фігури пішла від грецького слова «конос», так греки називали ялинкову шишку. Конус

Конус серед нас

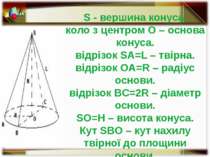
Конус – це тіло, отримане обертанням прямокутного трикутника навколо прямої, яка є нерухомим катетом. Це є одна з фігур обертання

КОНУС OK=H OA=OB=OC=R KA= KB= KD= l О А В К С D E F G

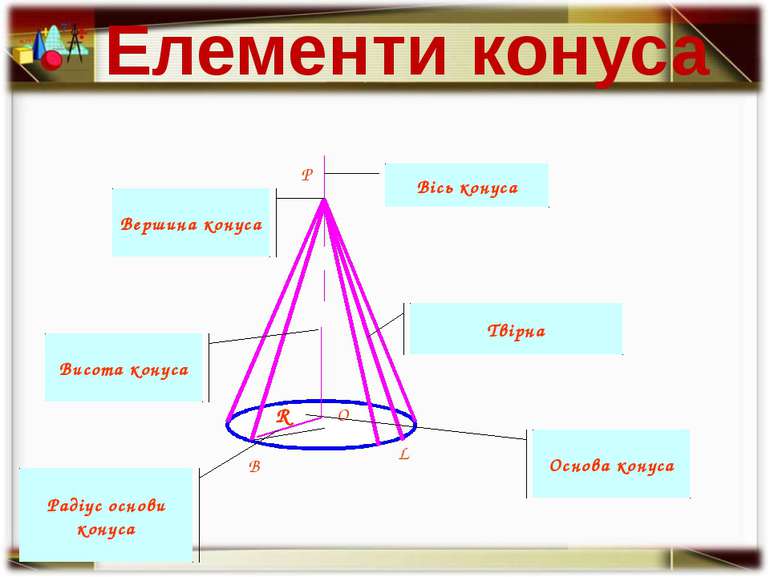
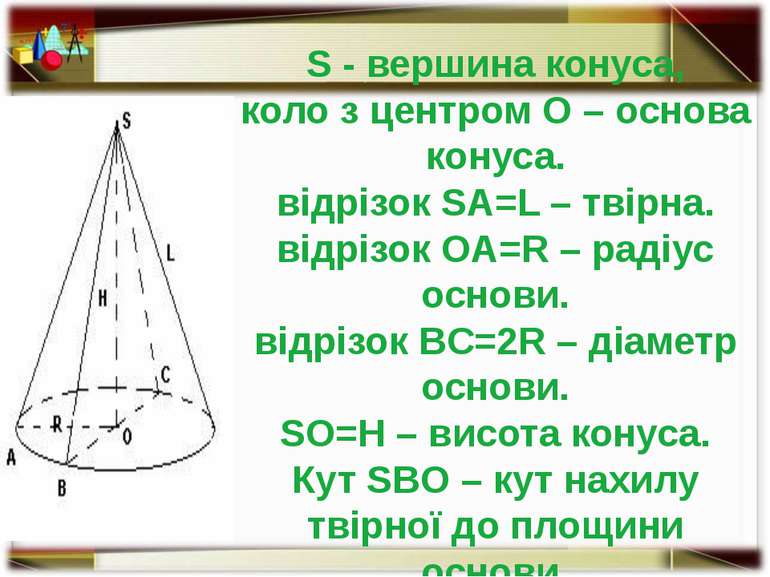
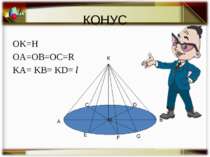
B P O R L Вісь конуса Вершина конуса Твірна Основа конуса Висота конуса Радіус основи конуса Елементи конуса

Електронний методичний посібник розділ 6, урок 6 блок 1,2,3

Розмітка БІЧНОЇ ПОВЕРХНІ КОНУСА – AK = r ПЛОЩА КРУГА: S = πr2

ФОРМУЛА ПЛОЩІ БІЧНОЇ ПОВЕРХНІ КОНУСА: Sб. = π R l R – радіус основи, l –твірна конуса.

ФОРМУЛА ПЛОЩІ ПОВНОЙ ПОВЕРХНІ КОНУСА Sп = Sб + Sосн Sп = πRl + π R2 Sп = π R(R+l) О К А В

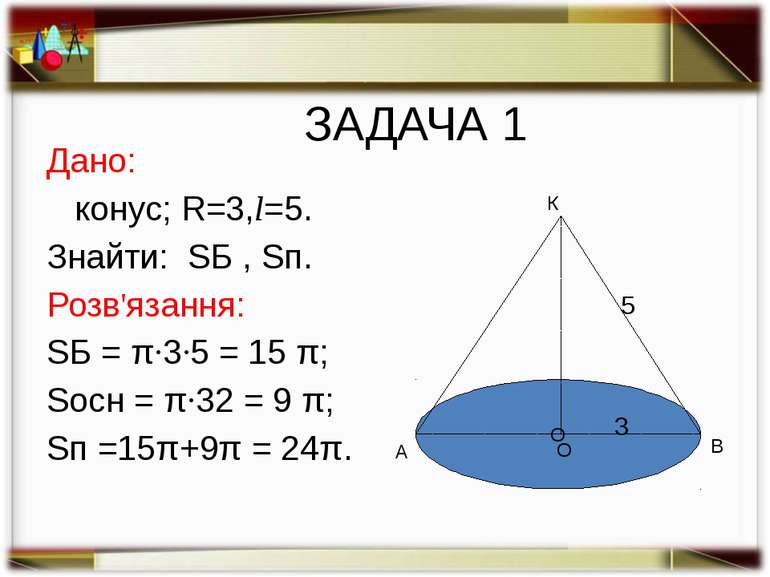
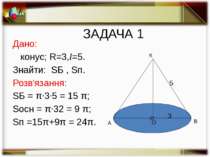
ЗАДАЧА 1 Дано: конус; R=3,l=5. Знайти: SБ , Sп. Розв'язання: SБ = π·3·5 = 15 π; Sосн = π·32 = 9 π; Sп =15π+9π = 24π. О А В К 3 5 О

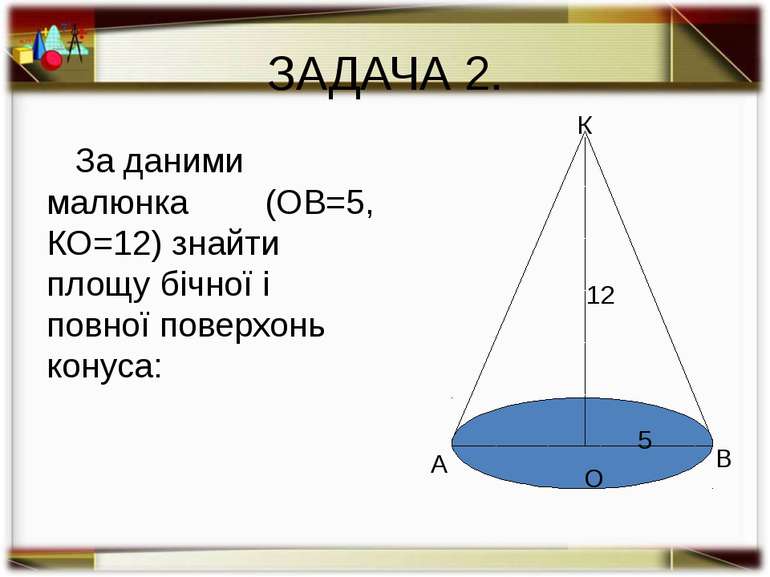
ЗАДАЧА 2. За даними малюнка (ОВ=5, КО=12) знайти площу бічної і повної поверхонь конуса: А О В К 5 12

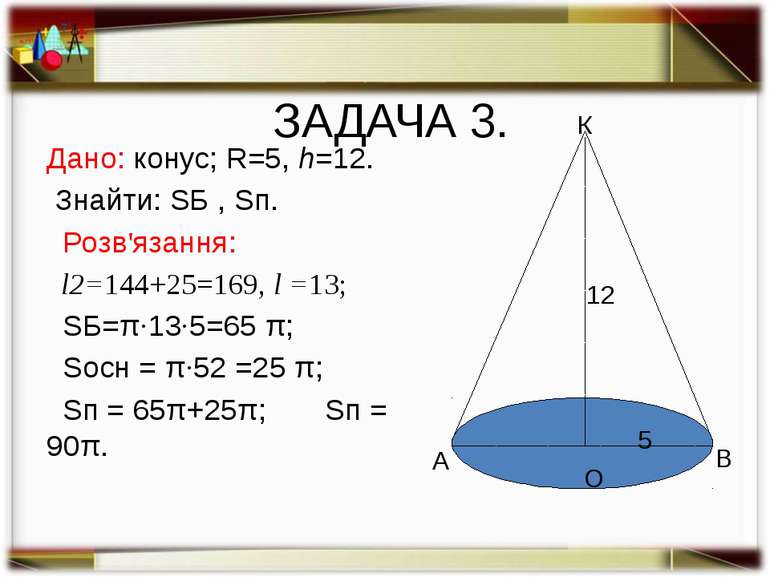
ЗАДАЧА 3. Дано: конус; R=5, h=12. Знайти: SБ , Sп. Розв'язання: l2=144+25=169, l =13; SБ=π·13·5=65 π; Sосн = π·52 =25 π; Sп = 65π+25π; Sп = 90π. О В К 5 12 А

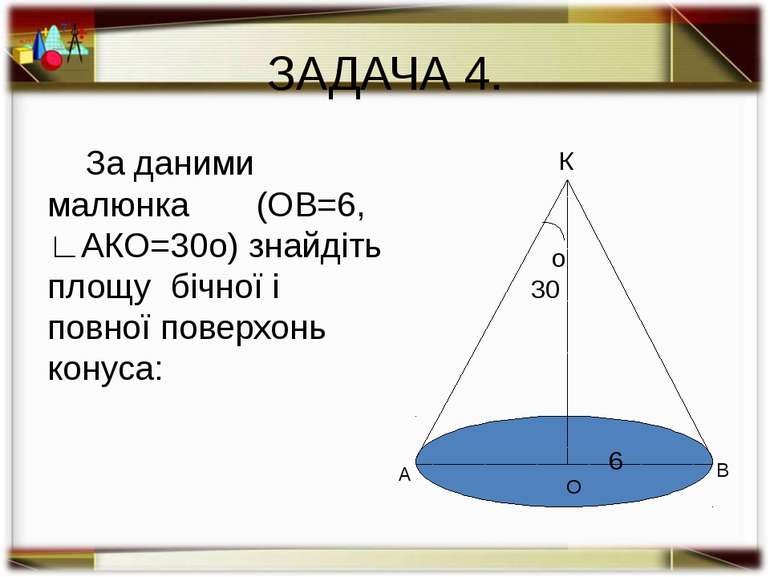
ЗАДАЧА 4. За даними малюнка (ОВ=6, ∟АКО=30о) знайдіть площу бічної і повної поверхонь конуса: о 30 К А В О 6

ЗАДАЧА 5. Дано: конус; R=6,∟АКО=30о. Знайти: SБ , Sп. Розв'язання: l = R/sin30о,l=6/0.5=12; SБ= π·12·6=72π; Sосн = π·62 =36π; Sп = 72π+36π; Sп = 108π. о 30 К А В О 6

ПРАКТИЧНА РОБОТА

ДЯКУЮ за урок!