Презентація на тему:
Многокутники

Геометрія 8 клас Многокутники

Мотивація вивчення теми Многокутники та його елементи. Опуклі та неопуклі многокутники Сума кутів опуклого многокутника Поняття площі. Властивості площі. Площа прямокутника Площа паралелограма Площа трикутника Площа трапеції Площі многокутників Тематична контрольна робота

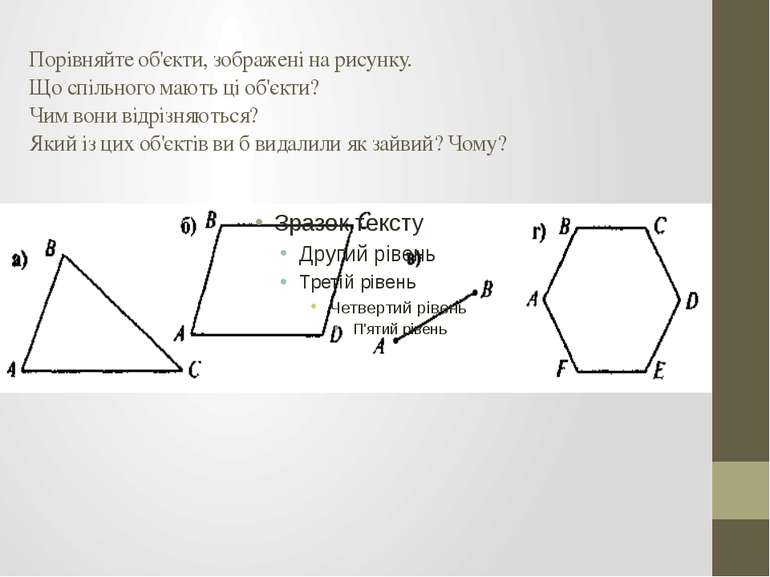
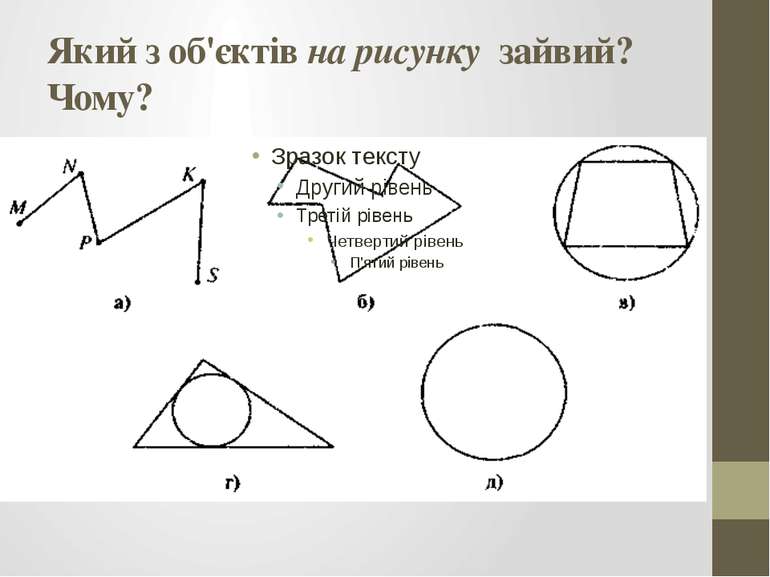
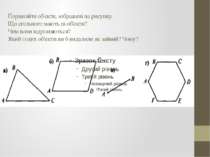
Порівняйте об'єкти, зображені на рисунку. Що спільного мають ці об'єкти? Чим вони відрізняються? Який із цих об'єктів ви б видалили як зайвий? Чому?

Тема уроку: Многокутник та його елементи. Опуклі та неопуклі многокутники

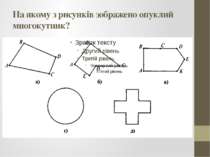
Актуалізація опорних знань Якою геометричною фігурою є вершина чотирикутника? Якою геометричною фігурою є сторона трикутника, чотирикутника? Що називають діагоналлю чотирикутника? Як називається геометрична фігура на рисунку

Актуалізація опорних знань Виконання усних вправ

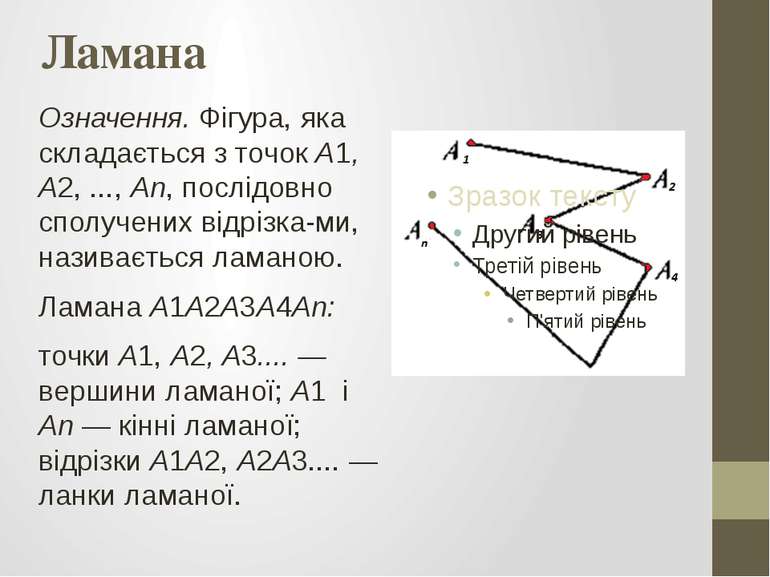
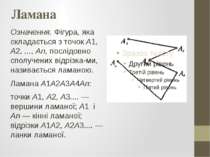
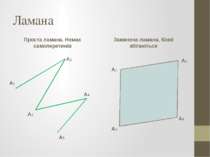
Ламана Означення. Фігура, яка складається з точок А1, А2, ..., Аn, послідовно сполучених відрізка ми, називається ламаною. Ламана А1А2А3А4Аn: точки А1, А2, А3.... — вершини ламаної; А1 і Аn — кінні ламаної; відрізки А1А2, А2А3.... — ланки ламаної.

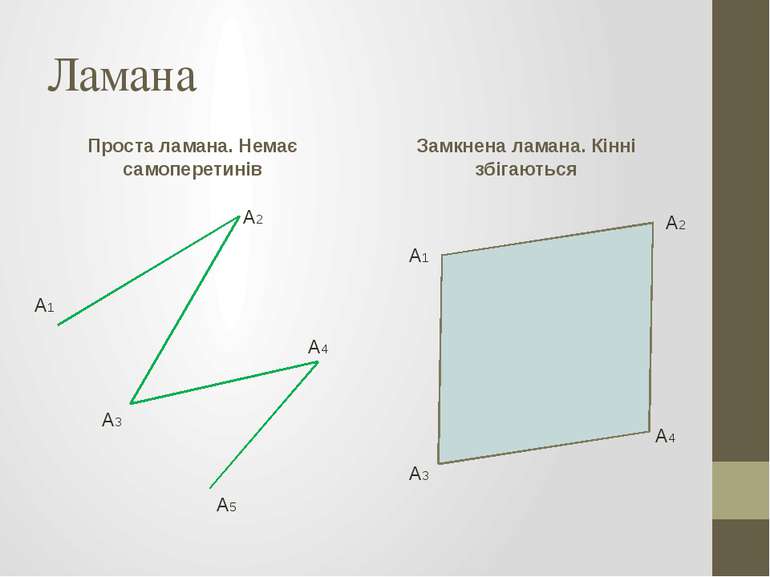
Ламана Проста ламана. Немає самоперетинів Замкнена ламана. Кінні збігаються А1 А2 А3 А4 А5 А1 А2 А3 А4

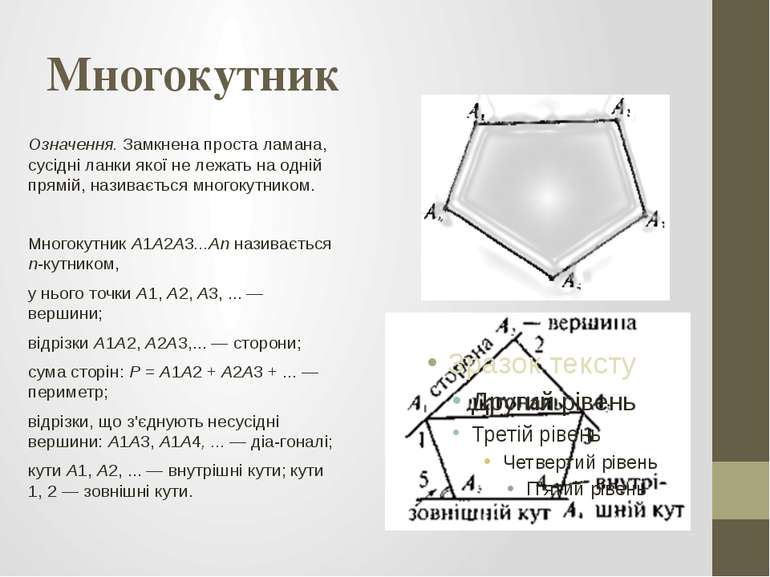
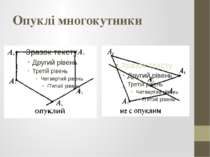
Многокутник Означення. Замкнена проста ламана, сусідні ланки якої не лежать на одній прямій, називається многокутником. Многокутник А1А2А3...Аn називається n-кутником, у нього точки А1, А2, А3, ... — вершини; відрізки А1А2, А2А3,... — сторони; сума сторін: Р = А1А2 + А2А3 + ... — периметр; відрізки, що з'єднують несусідні вершини: А1А3, A1A4, ... — діа гоналі; кути А1, А2, ... — внутрішні кути; кути 1, 2 — зовнішні кути.

Опуклі многокутники

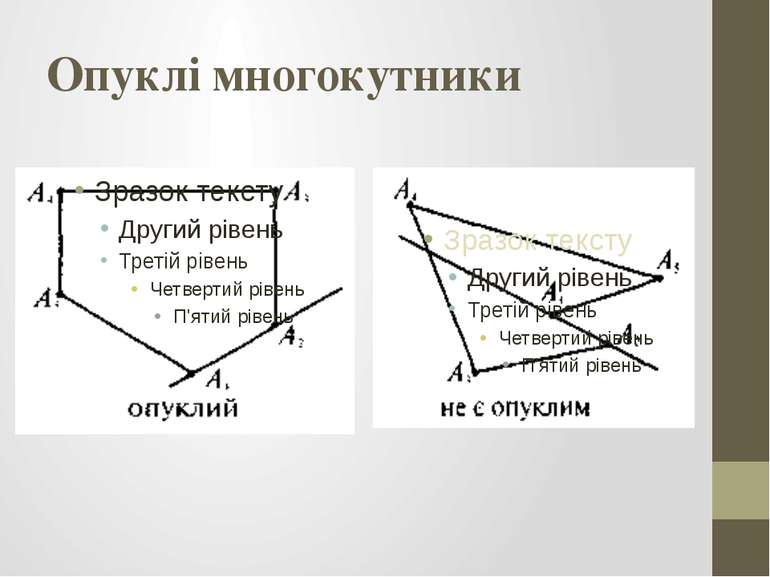
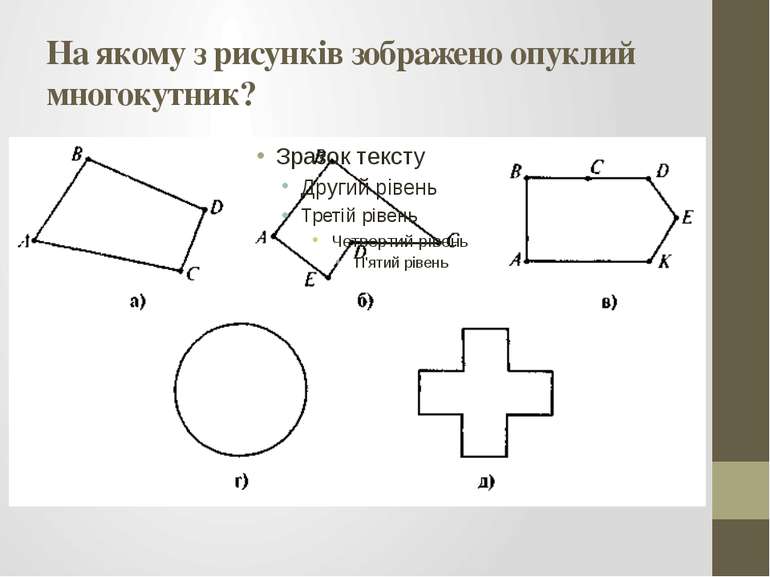
Властивості (опуклих) многокутників В опуклому n-кутнику: 1) із кожної вершини можна провести (n – 3) діагоналі; 2) кількість усіх діагоналей дорівнює ; 3) для будь-якої сторони а справедливо, що а < Р (Р — пери метр n-кутника); 4) сума внутрішніх кутів Sn = 180°(n – 2); 5) сума зовнішніх кутів, взятих по одному при кожній вершині — 360°; 6) якщо всі сторони і всі кути рівні, то n-кутник с правильним, і тоді (Р = аn, Р — периметр; а — сторона); — внутрішній кут; — зовнішній кут

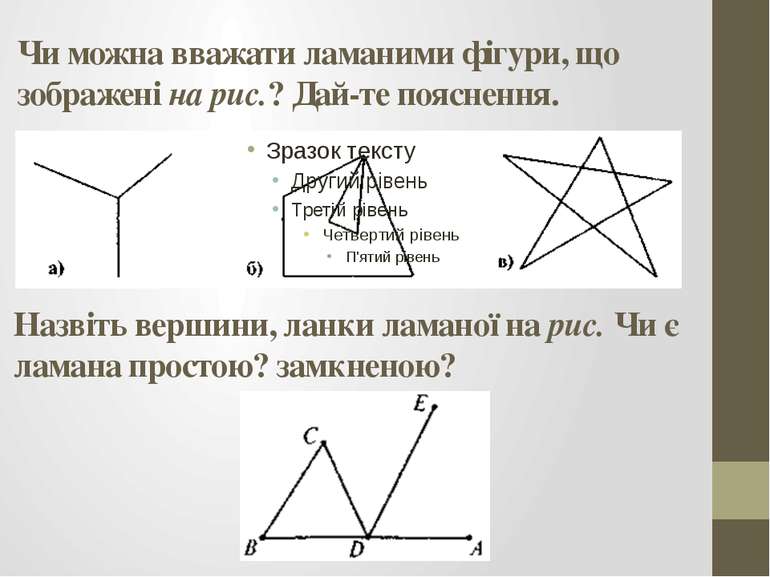
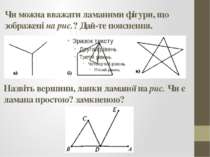
Чи можна вважати ламаними фігури, що зображені на рис.? Дай те пояснення. Назвіть вершини, ланки ламаної на рис. Чи є ламана простою? замкненою?

На якому з рисунків зображено опуклий многокутник?

Усні вправи 1). Скільки діагоналей виходить з однієї вершини семикутника? 2). Чи може діагональ шестикутника ділити його: а) на два трикутники; б) на два чотирикутники; в) на трикутник і п'ятикутник? 3). Діагональ відтинає від п'ятикутника чотирикутник. Який вид має частина, що залишилася?

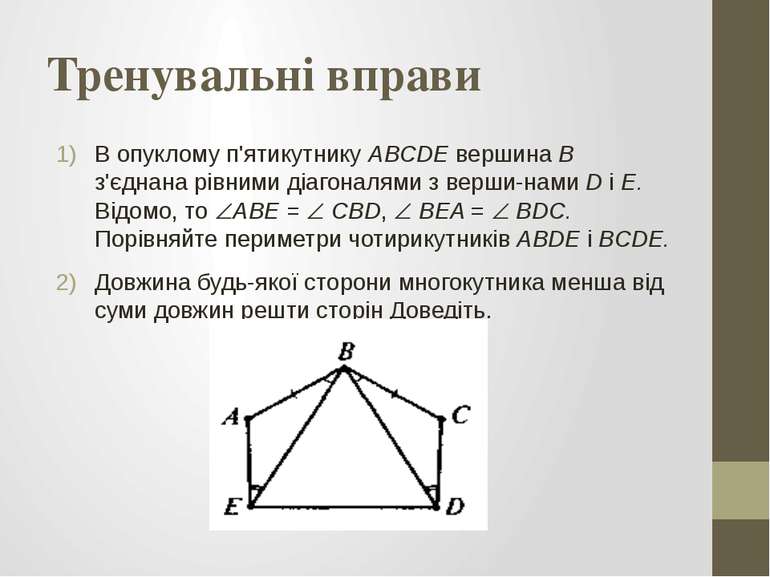
Тренувальні вправи В опуклому п'ятикутнику ABCDE вершина В з'єднана рівними діагоналями з верши нами D і Е. Відомо, то ABE = CBD, BEA = BDC. Порівняйте периметри чотирикутників ABDE і BCDE. Довжина будь-якої сторони многокутника менша від суми довжин решти сторін Доведіть.

Який з об'єктів на рисунку зайвий? Чому?