Презентація на тему:
Многокутники

що таке многокутник, його різновиди; як знайти суму кутів опуклого многокутника; як знаходиться площа паралелограма, трикутника, описаного чотирикутника, тощо.

Многокутником називається частина площини, обмежена відрізками А1А2, А2А3, …, Аn-1Аn, Аn А1. Точки А1, А2, А3,…, Аn називають вершинами многокутника, а вказані вище відрізки – сторонами многокутника. Сторони, що є сусідніми відрізками, називають сусідніми сторонами многокутника. Вершини, які належать одній стороні, називають сусідніми вершинами многокутника. Кут многокутника утворюється сусідніми сторонами многокутника. А2 А1 Аn Аn-1 А3 α β δ

Многокутник називають за кількістю його кутів: трикутник, чотирикутник, п'ятикутник тощо. Многокутник позначають за його вершинами як ABCDE. Периметром многокутника називають суму довжин усіх його сторін. Відрізок, який сполучає не сусідні вершини многокутника, називають діагоналлю CE. А E D C B

Многокутник називається опуклим, якщо усі його кути менші від розгорнутого. Властивості опуклого многокутника: опуклий многокутник розташований в одній півплощині відносно будь-якої прямої, що містить його сторону; опуклий многокутник містить будь-яку свою діагональ.

Теорема 19.1. Сума кутів опуклого n-кутника дорівнює 180˚∙(n-2) На рисунку зображено опуклий n-кутник А1А2А3…Аn. Проведемо всі його діагоналі, які проходять через вершину А1. Ці діагоналі розбивають даний многокутник на n-2 трикутники. Сума всіх кутів цих трикутників дорівнює сумі кутів n-кутника. Оскільки сума кутів кожного трикутника дорівнює 180˚, то шукана сума дорівнює 180˚∙(n-2). Теорема справедлива для всіх многокутників. Аn Аn-1 А3 А2 А1

Многокутник називається вписаним, якщо: існує коло, якому належать усі його вершини; серединні перпендикуляри всіх сторін многокутника перетинаються в одній точці. Многокутник називають описаним, якщо: існує коло, яке дотикається до всіх його сторін; бісектриси всіх кутів многокутника перетинаються в одній точці.

Площею многокутника називають величину, яка має такі властивості: рівні многокутники мають рівні площі; якщо многокутник складено з кількох многокутників, то його площа дорівнює сумі площ цих многокутників; за одиницю виміру площі приймають площу одиничного квадрата, тобто квадрата зі стороною, яка дорівнює одиниці виміру довжини.

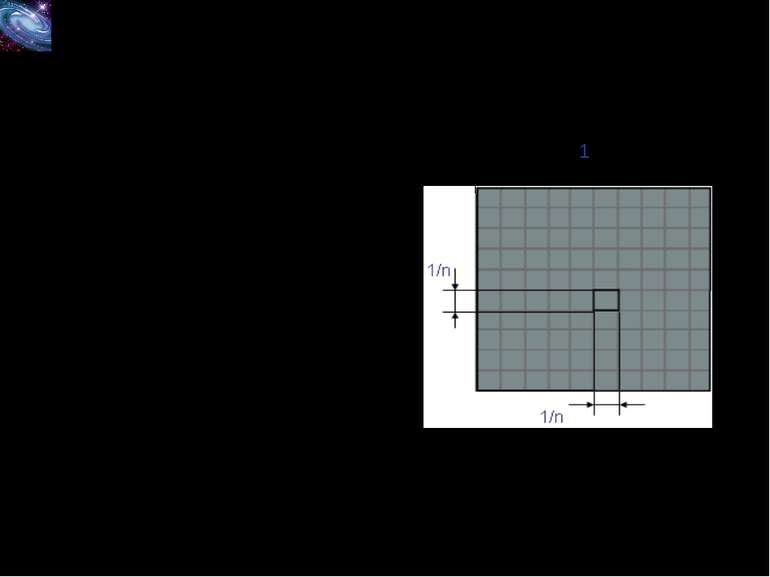
Лема. Площа квадрата зі стороною 1/n од (n – натуральне число) дорівнює 1/n2 од2. Доведення. Розглянемо одиничний квадрат і поділимо його на n2 рівних квадратів зі стороною 1/n. З означення площі многокутника (властивість 1) випливає, що всі ці квадрати мають рівні площі. За властивістю 2 сума площ цих квадратів дорівнює площі одиничного квадрата, тобто дорівнює 1 од2. Тому площа кожного маленького квадрата дорівнює 1/n2 од2. 1

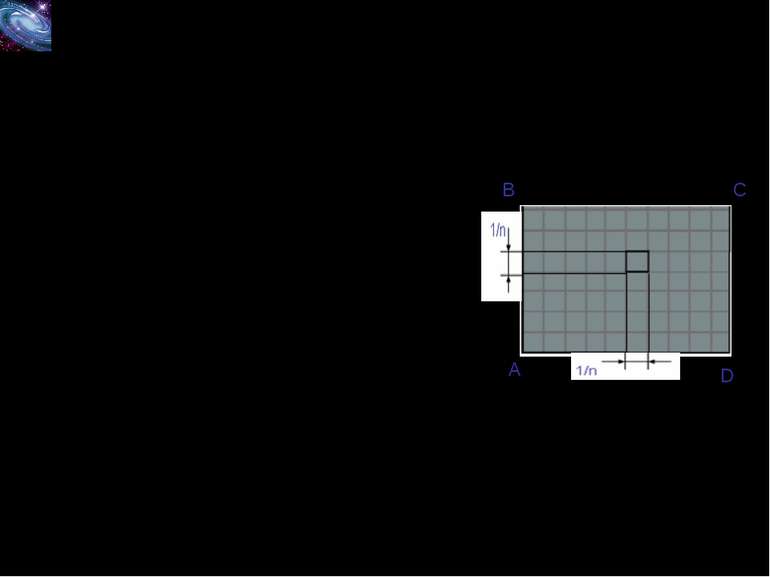
Теорема 20.1. Площа прямокутника дорівнює добутку довжин його сусідніх сторін Доведення. На рисунку зображено прямокутник ABCD, довжини сусідніх сторін якого дорівнюють a і b: AB=a, BC=b. Доведемо, що площа S прямокутника обчислюється за формулою S=ab. Нехай a і b – раціональні числа. Тоді ці числа можна подати у вигляді звичайних дробів, які зведено до однакових знаменників. Маємо a=p/n, b=q/n, де p, q, n – натуральні числа. Поділимо сторону AB на p рівних частин, а BC – на q. Через точки поділу проведемо прямі, паралельні сторонам прямокутника. Тоді прямокутник буде поділено на pq рівних квадратів зі стороною 1/n. Згідно з лемою площа кожного квадрата дорівнює 1/n2. З означення площі (властивість 2) випливає, що площа прямокутника дорівнює сумі площ усіх квадратів, тобто B C D А q частин p частин

Наслідок (площа квадрата) Площа квадрата дорівнює квадрату його сторони: S=a2, де a – сторона квадрата. a

Многокутники, які мають рівні площі, називають рівновеликими.

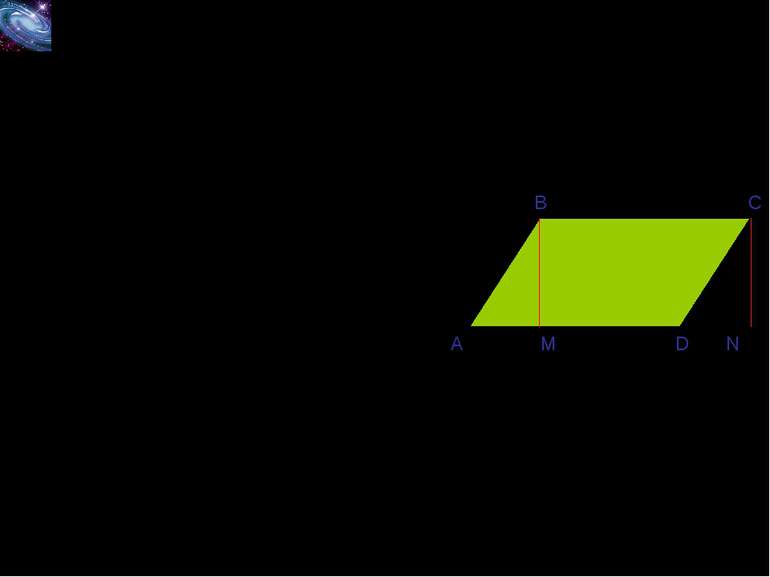
Теорема 21.1. Площа паралелограма дорівнює добутку його сторони на висоту, яка відповідає цій стороні Доведення. На рисунку зображено паралелограм ABCD, площа якого дорівнює S. Проведемо дві висоти BM i CN. Доведемо, що S=BM·BC. Покажемо, що MBCN (прямокутник) є рівновеликим даному паралелограму. Очевидно, що SABCD=SABM+SMBCD; SMBCN=SDCN+SMBCD; ∆ABM=∆DCN(тобто рівновеликі); З наведених міркувань слідує, що паралелограм ABCD i прямокутник MBCN рівновеликі. За теоремою 20.1 площа прямокутника дорівнює добутку BM∙BC. Тоді S=BM·BC, де S – площа паралелограма ABCD. А B M D C N

Теорема 22.1. Площа трикутника дорівнює половині добутку його сторони на проведену до неї висоту Доведення. На рисунку зображено ∆ABC, площа якого S. Проведемо висоту BM. Доведемо, що S=1/2AC∙BM. Проведемо прямі BNllAC i CNllAB. Тоді видно, що ABNC – паралелограм, а ∆ABC= ∆NBC (як і площі відповідно). Отже SABC=1/2SABN, звідки слідує, що SABC=1/2AC·BM. M C N B A

Наслідок №1 Площа прямокутного трикутника дорівнює половині добутку його катетів: S=1/2ab, де a і b – катети прямокутного трикутника. b a

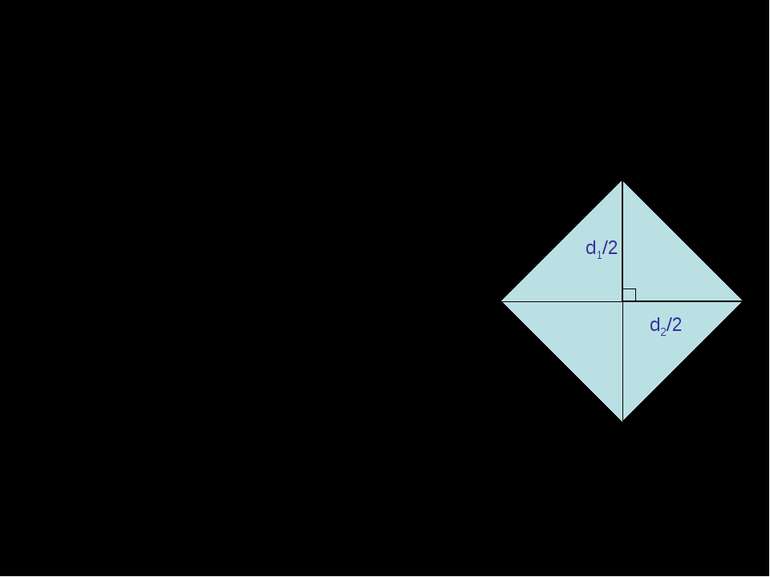
Наслідок №2 Площа ромба дорівнює половині добутку його діагоналей: S=1/2d1d2, де d1 і d2 – діагоналі ромба. Дійсно, діагоналі ділять ромб на чотири рівні прямокутні трикутники з катетами 1/2d1 і 1/2d2. Користуючись попереднім наслідком, маємо: d1/2 d2/2

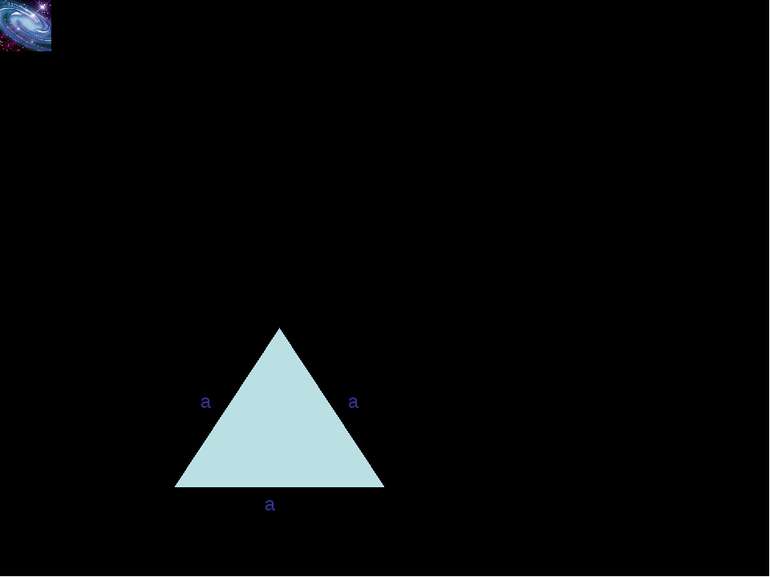
Наслідок №3 Площа рівностороннього трикутника зі стороною a обчислюється за формулою: a a a

Теорема 23.1. Площа трапеції дорівнює добутку півсуми її основ на висоту Доведення. На рисунку зображено трапецію ABCD, площа якої S. Проведемо діагональ AC та висоти для ∆ABC і ∆ACD (HA=CF=h). Тоді ми отримаємо: D C H B A F

Контроль знань Тестова частина: Многокутником називається … Діагональ – це … Поставити у відповідність поняття до їх означень: описаний многокутник; опуклий многокутник; вписаний многокутник; не опуклий многокутник; лежить по один бік від будь-якої прямої, що містить його сторону; всі вершини лежать на колі; лежить по обидві сторони від хоча б одної прямої, яка містить його сторону; всі сторони дотикаються до кола.

Тестова частина: Сума кутів опуклого n-кутника дорівнює: 180˚(n); 180˚(n-1); 180˚(n-2); 180˚(n+1). Скільки діагоналей виходять з однієї вершини семикутника: 5; 4; 6; 7. Вказати правильні аксіоми площ (їх три): рівновеликі многокутники мають не рівні площі; площа многокутника рівна подвійному периметру; площа квадрата зі стороною, що дорівнює одиниці довжини, дорівнює одиниці площі; якщо многокутник складений із кількох многокутників, то його площа дорівнює сумі площ цих многокутників; рівновеликі многокутники є рівними фігурами; рівні многокутники мають рівні площі.

Тестова частина: Встановити відповідність між поняттям і формулою: площа трикутника; площа квадрата; площа трапеції; площа ромба; площа прямокутника; площа прямокутного трикутника; площа паралелограма; 2 1 3 5 7 4 6

Практична частина: Варіант №1: Задача №1. Знайдіть площу рівнобедреного трикутника з периметром 16 см і висотою, довжина якої 4 см, поведеною до основи. Задача №2. Площа паралелограма дорівнює 36 см2, а довжини його висот 3 см і 4 см. Знайдіть периметр паралелограма. Задача №3. Основи трапеції дорівнюють 10 см і 35 см, а бічні сторони – 15 см і 20 см. Знайдіть площу трапеції.

Практична частина: Варіант №2: Задача №1. Знайдіть площу ромба з периметром 24 см і тупим кутом 150˚. Задача №2. Знайдіть площу рівнобедреної трапеції з бічною стороною 10 см, описаної навколо кола з радіусом 4 см. Задача №3. У трапеції ABCD основи BC і AD дорівнюють 2 см і 8 см відповідно. Діагоналі трапеції перетинаються в точці О. Знайдіть площі трикутників ВОC i АОD; площу трапеції ABCD.

Практична частина: Варіант №3: Задача №1. Бісектриса прямокутного трикутника ділить гіпотенузу на відрізки завдовжки 15 см і 20 см. Знайти площу трикутника. Задача №2. Висота ромба з тупим кутом 150˚ дорівнює 5 см. Знайдіть площу ромба. Задача №3. У паралелограмі ABCD діагональ BD є висотою, кут А=45˚, AD=4 см. Знайдіть площі трикутників ABC i BCD.