Презентація на тему:
Геометрія. Многокутники

Дудник Н.М.

Многокутники. Означення многокутника. Елементи многокутника. Властивість кутів многокутника. Означення правильних многокутників. Вписані та описані многокутники. Елементи правильних многокутників Формули для обчислення площі правильного многокутника, його сторони, радіусів вписаного та описаного кола. Зміст навчального матеріалу Дудник Н.М.

многокутники Дудник Н.М.

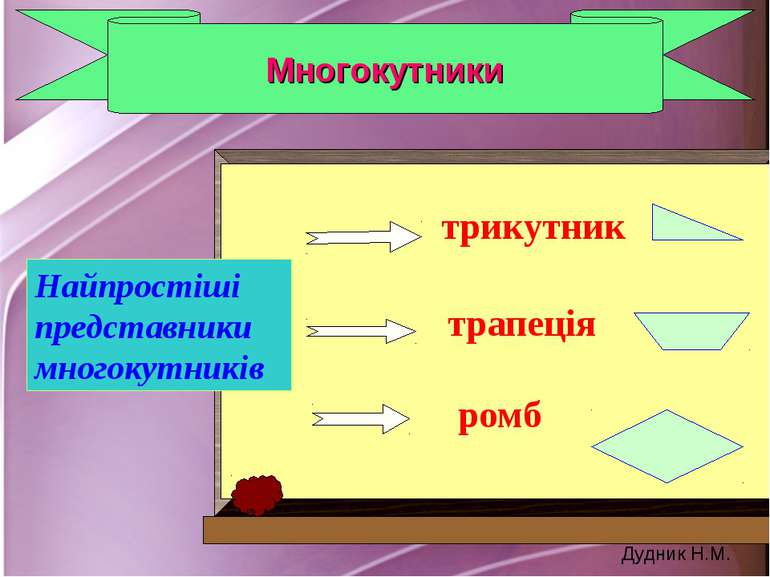
Многокутники Об’єднання простої замкненої ламаної та її внутрішньої області називається многокутником. Дудник Н.М.

Многокутники Найпростіші представники многокутників трикутник трапеція ромб Дудник Н.М.

многокутники Многокутник називається опуклим, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону. При цьому сама пряма вважається такою, що належить півплощині. Опуклий многокутник Неопуклий многокутник Дудник Н.М.

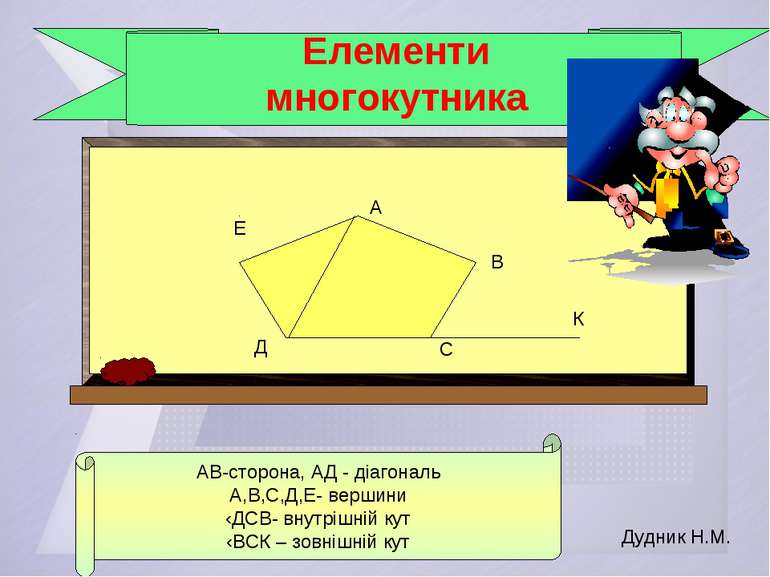
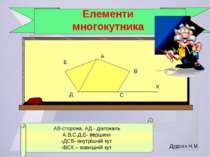
Ланки ламаної називаються сторонами многокутника. Точки, в яких збігаються дві суміжні ланки, називаються вершинами многокутника. Кути, утворені двома суміжними сторонами многокутника, називаються внутрішніми кутами многокутника. Кути, суміжні з внутрішніми кутами многокутника, називаються його зовнішніми кутами. Відрізок, що з’єднує дві вершини, які не належать одній з його сторін називається діагоналлю. Сума довжин усіх сторін многокутника називається його периметром. Дудник Н.М.

АВ-сторона, АД - діагональ А,В,С,Д,Е- вершини ‹ДСВ- внутрішній кут ‹ВСК – зовнішній кут А В С Д Е К Елементи многокутника Дудник Н.М.

Властивість кутів многокутника Дудник Н.М.

ПРАВИЛЬНІ МНОГОКУТНИКИ. Дудник Н.М.

Правильні многокутники Правильним називається опуклий многокутник, в якого всі кути і всі сторони рівні. Найпростіші приклади правильних многокутників є рівносторонній трикутник, квадрат. Дудник Н.М.

Вписані та описані многокутники Многокутник називається вписаним у коло, якщо всі його вершини лежать на колі (коло описане). Многокутник називається описаним, якщо всі сторони многокутника дотикаються до цього кола (коло вписане) Вписане й описане кола правильного многокутника мають один і той самий центр. Дудник Н.М.

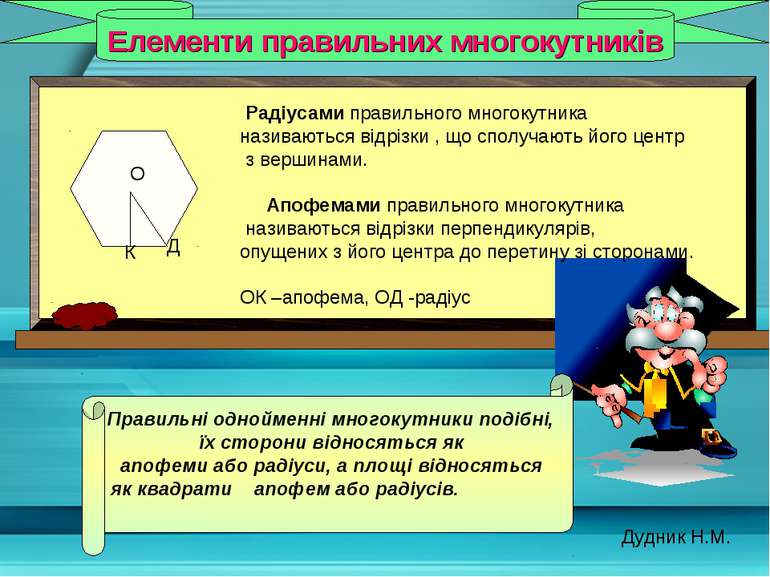
Елементи правильних многокутників Правильні однойменні многокутники подібні, їх сторони відносяться як апофеми або радіуси, а площі відносяться як квадрати апофем або радіусів. О К Радіусами правильного многокутника називаються відрізки , що сполучають його центр з вершинами. Апофемами правильного многокутника називаються відрізки перпендикулярів, опущених з його центра до перетину зі сторонами. ОК –апофема, ОД -радіус Дудник Н.М. Д

ПРАВИЛЬНІ МНОГОКУТНИКИ ПОЗНАЧЕННЯ Нехай S – площа правильного n-кутника, n— його сторона, r і R радіуси відповідно вписаного і описаного кіл. загальні формули радіусів вписаного та описаного кіл Дудник Н.М.

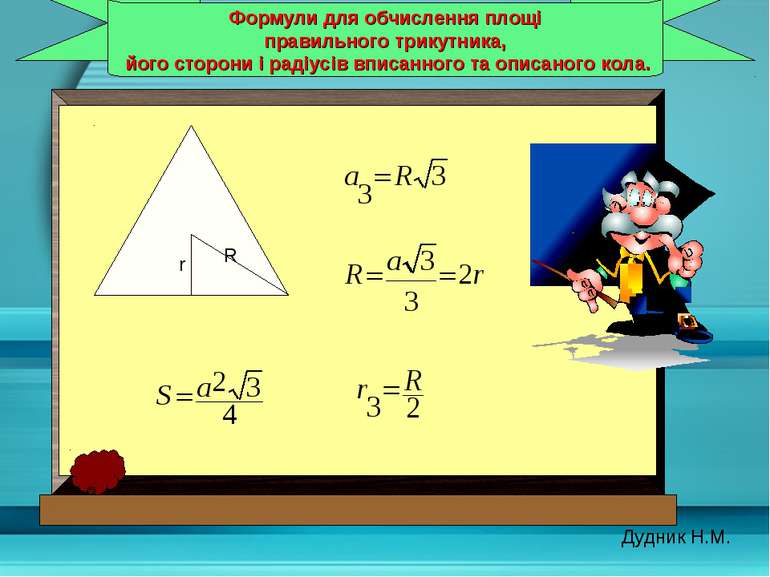
Формули для обчислення площі правильного трикутника, його сторони і радіусів вписанного та описаного кола. Дудник Н.М. r R

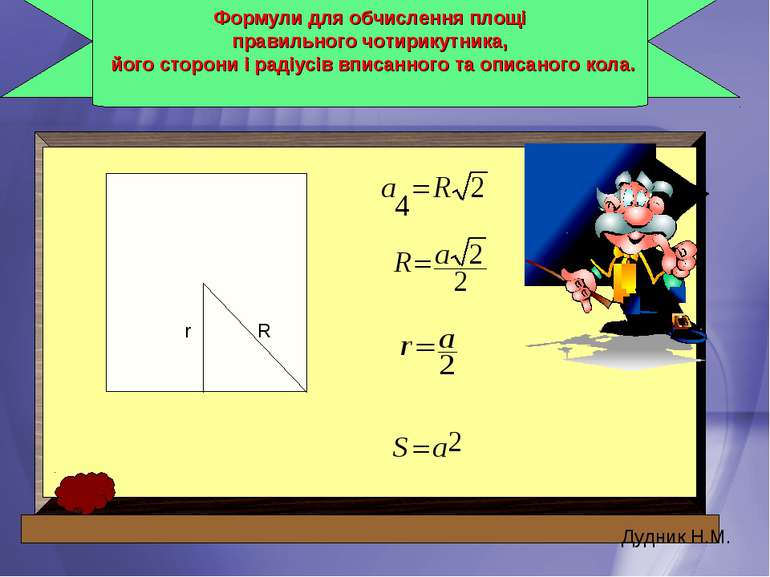
Формули для обчислення площі правильного чотирикутника, його сторони і радіусів вписанного та описаного кола. r Дудник Н.М. R

Формули для обчислення площі правильного п’ятикутника, його сторони і радіусів вписанного та описаного кола. Дудник Н.М. r R

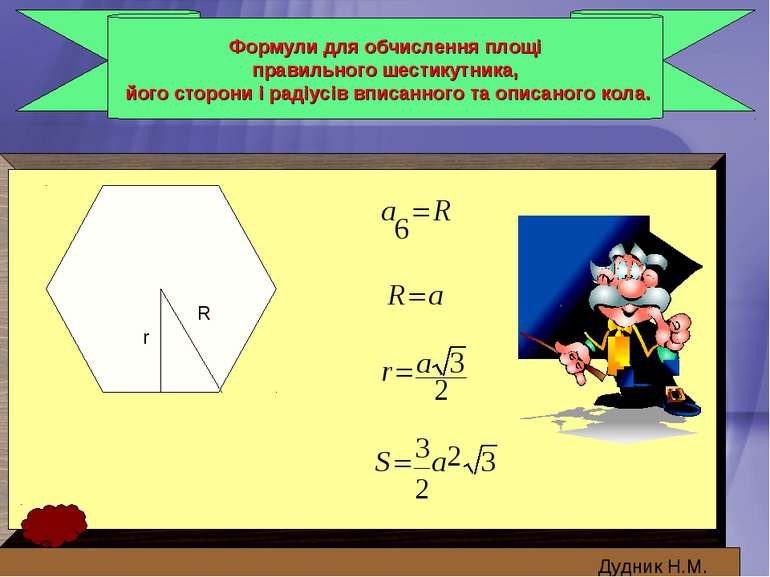
Формули для обчислення площі правильного шестикутника, його сторони і радіусів вписанного та описаного кола. Дудник Н.М. r R

Формули для обчислення площі правильного восьмикутника, його сторони і радіусів вписанного та описаного кола. Дудник Н.М. r R