Презентація на тему:
Геометрія Лобачевського та теорія відносності Ейнштейна

Геометрія Лобачевського та теорія відносності Ейнштейна Грані стикання

Альберт Ейнштейн - видатний фізик, творець теорії відносності, один із творців квантової теорії і статистичної фізики. З 1909 року - професор Цюрихського університету, а потім — Німецького університету в Празі. З 1914 р. – професор Берлінського університету, де завершив створення загальної теорії відносності, розвив квантову теорію випромінювання. За відкриття законів фотоефекта і роботи в області теоретичної фізики Ейнштейн одержав у 1921 р. Нобелівську премію. Альберт Ейнштейн (1879-1955) Учений працював і над створенням єдиної теорії поля, що поєднує гравітаційні й електромагнітні взаємодії. Наукові праці Ейнштейна зіграли велику роль у розвитку сучасної фізики – квантової електродинаміки, атомної і ядерної фізики, фізики елементарних часток, космології, астрофізики.

Стаття Ейнштейна "До електродинаміки тіл, що рухаються" (1905) окреслила засади спеціальної теорії відносності, основні постулати якої: В усіх інерційних системах відліку фізичні процеси відбуваються однаково. Швидкість світла у вакуумі не залежить від руху джерела або приймача і однакова в усіх напрямах.

Що сприяло виникненню цієї гіпотези? Наприкінці 19-го століття фізика зіткнулася з проблемою: неможливістю експериментально визначити швидкість руху Землі відносно ефіру, а, отже, й експериментально підтвердити гіпотезу існування ефіру, на якій ґрунтувалася електродинаміка. Основні рівняння електродинаміки, побудовані на основі припущення, що електромагнітні хвилі розповсюджуються в певній невагомій речовині, здавалося мали сенс лише в системі відліку, жорстко зв'язаній з цією речовиною. Досліди Майкельсона (1887) показали, що ефіру, мабуть, не існує. Згодом були відкриті перетворення, відносно яких система основних рівнянь електродинаміки є інваріантною. Ці перетворення отримали назву перетворень Лоренца.

В 1905 році Альберт Ейнштейн сміливо постулював справедливість рівнянь електродинаміки в будь-якій інерційній системі відліку. Таким чином, фундаментальна стала - швидкість світла - однакова для будь-якої інерційної системи відліку, а от довжина і час змінюються при переході від однієї системи до іншої за законом, який задають перетворення Лоренца. Відповідно, будь-який закон фізики повинен бути лоренц-інваріантним, включно із законами Ньютона, які повинні бути записані з врахуванням зміни в поняттях довжини і часу. При малих швидкостях ці зміни дуже незначні і починають проявлятися лише при швидкостях, близьких до швидкості світла.

Наслідком спеціальної теорії відносності є принцип причинності. Будь-яка інформація не може передаватися зі швидкістю, що перевищувала б швидкість світла у вакуумі, інакше завжди знайшлася б система відліку, в якій наслідок передував би причині. Оскільки фізичні тіла не можуть рухатися зі швидкістю, більшою за швидкість світла, при наближенні до швидкості світла маса будь-якого тіла необмежено зростає.

З точки зору спеціальної теорії відносності простір і час тісно пов'язані між собою. Їх слід вважати єдиним чотиривимірним многовидом, що має назву „простір-час”. Спостерігачі, що рухаються один відносно одного, по-різному визначають "просторові" і "часовий" напрямки у цьому многовиді. Тому простір і час більше неможливо розглядати як дві окремі сутності. Загальна теорія відносності доповнила цю картину тим, що енергія гравітаційного поля (породжена матерією) здатна деформувати простір-час так, що „прямі” лінії в просторі та часі мають властивості „кривих” ліній.

Математики використовують термін „викривлення” для позначення будь-якого простору, де геометрія не є Евклідовою.

Німецький математик Фелікс Клейн в ХІХ ст. довів таку важливу для нас теорему: Якщо в просторі можливі довільні зсуви і повороти, то це може бути тільки а) простір сталої додатної кривизни з звичайною сферичною геометрією (сума кутів трикутника більша двох прямих); б) плоский простір з нульовою кривизною і геометрією Евкліда (сума кутів трикутника дорівнює двом прямим); в) простір сталої від'ємної кривизни (сума кутів трикутника менша двох прямих).

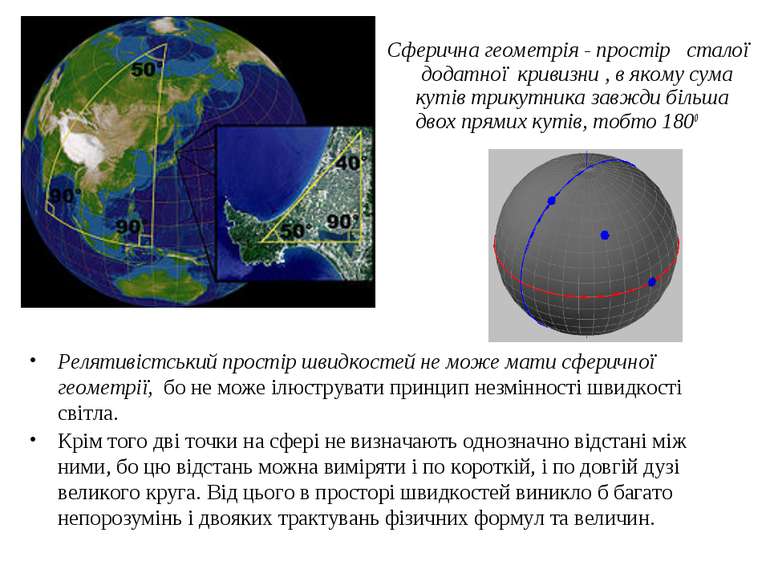
Релятивістський простір швидкостей не може мати сферичної геометрії, бо не може ілюструвати принцип незмінності швидкості світла. Крім того дві точки на сфері не визначають однозначно відстані між ними, бо цю відстань можна виміряти і по короткій, і по довгій дузі великого круга. Від цього в просторі швидкостей виникло б багато непорозумінь і двояких трактувань фізичних формул та величин. Сферична геометрія - простір сталої додатної кривизни , в якому сума кутів трикутника завжди більша двох прямих кутів, тобто 1800

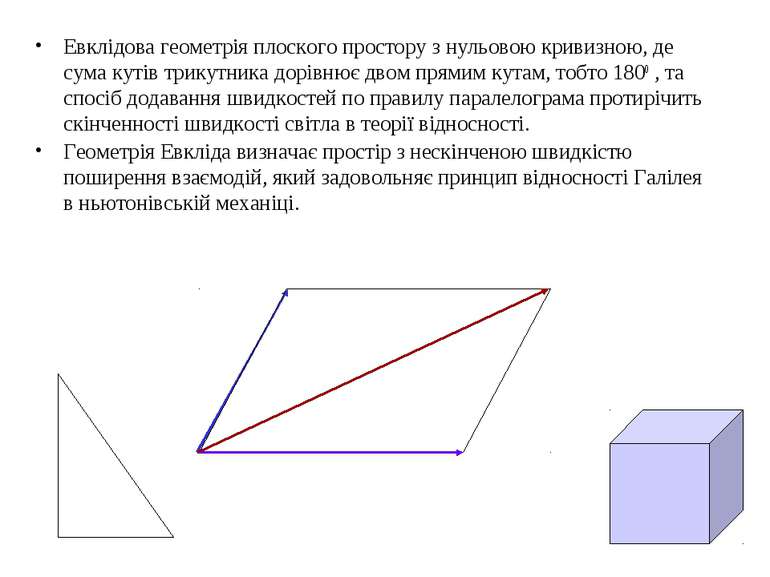
Евклідова геометрія плоского простору з нульовою кривизною, де сума кутів трикутника дорівнює двом прямим кутам, тобто 1800 , та спосіб додавання швидкостей по правилу паралелограма протирічить скінченності швидкості світла в теорії відносності. Геометрія Евкліда визначає простір з нескінченою швидкістю поширення взаємодій, який задовольняє принцип відносності Галілея в ньютонівській механіці.

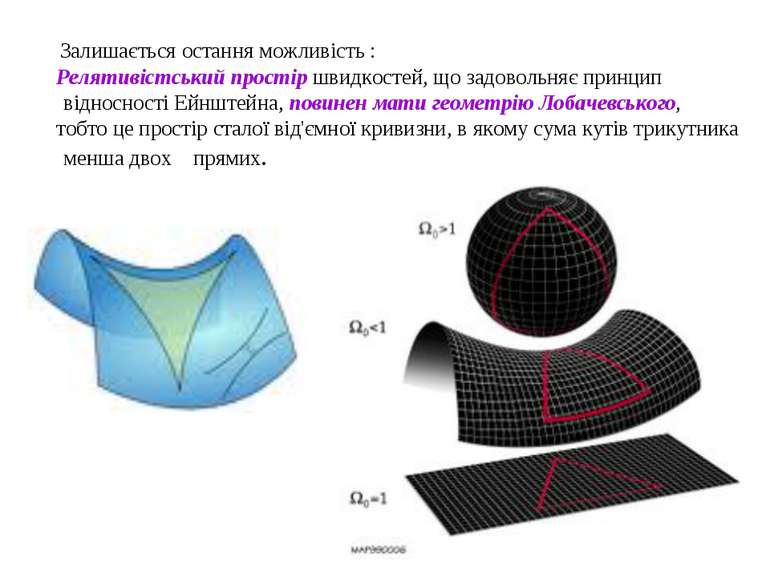
Залишається остання можливість : Релятивістський простір швидкостей, що задовольняє принцип відносності Ейнштейна, повинен мати геометрію Лобачевського, тобто це простір сталої від'ємної кривизни, в якому сума кутів трикутника менша двох прямих.

МИКОЛА ІВАНОВИЧ ЛОБАЧЕВСЬКИЙ Микола Іванович Лобачевський (1792—1856 pp.) М. І. Лобачевський народився 1 грудня 1792 р. в Нижньому Новгороді у сім'ї повітового землеміра. Після закінчення Казанської гімназії був зарахований до університету 14 лютого 1807 р. У 1814 р. Лобачевському було надано звання ад'юнкта (доцента), а ще через два роки—професора. З цього часу починається його тридцятирічна професорська діяльність у рідному університеті. У 1827 р. обраний ректором університету, який став центром освіти та наукової діяльності всього краю. Лобачевський як ректор користувався заслуженим авторитетом і повагою. Рада університету обирала його на цю посаду шість разів підряд (1827— 1846). Але світову славу вченого йому принесли геніальні дослідження в галузі геометрії. У 1829 p., Лобачевський опублікував у журналі «Казанский вестник», що видавався співробітниками університету, статтю «Про начала геометрії».

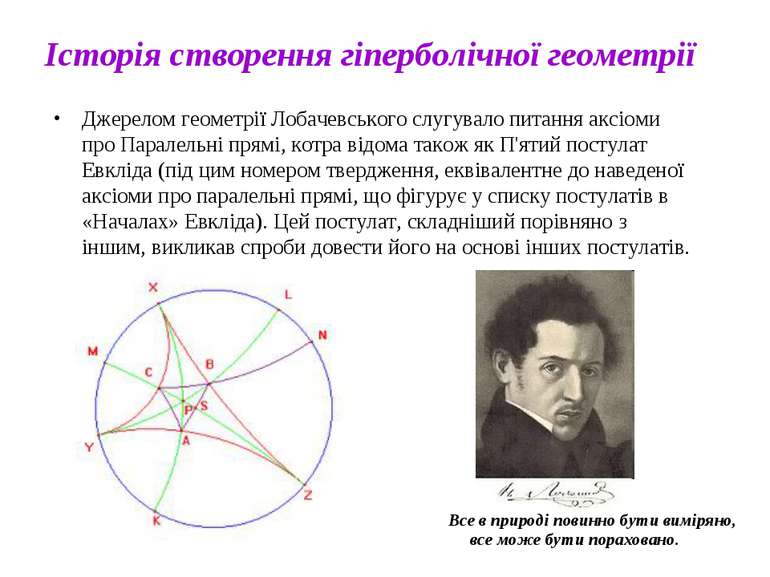
Історія створення гіперболічної геометрії Джерелом геометрії Лобачевського слугувало питання аксіоми про Паралельні прямі, котра відома також як П'ятий постулат Евкліда (під цим номером твердження, еквівалентне до наведеної аксіоми про паралельні прямі, що фігурує у списку постулатів в «Началах» Евкліда). Цей постулат, складніший порівняно з іншим, викликав спроби довести його на основі інших постулатів. Все в природі повинно бути виміряно, все може бути пораховано.

Історія створення гіперболічної геометрії Ось неповний список учених, що займались доведенням V постулату до XIX ст.: давньогрецькі математики Птолемей (II ст.), Прокл (V ст.) (доведення Прокла базується на припущенні скінченності відстані між двома паралельними), Ібн-аль-Хайсам з Іраку (кінець X ст. — початок XI ст.) (Ібн-аль-Хайсам намагався довести V постулат, виходячи з припущення, що кінець рухомого перпендикуляру до прямої описує прямую лінію), іранський математик Омар Хайям (друга половина XI — початок XII вв.), азербайджанський математик Насиреддин Тусі (XIII ст.) (Хайям та Насиреддин при доведенні V постулату виходили з припущення, що дві збіжні прямі не можуть при продовженні стати розбіжними при перетині), Омар Хайям

Історія створення гіперболічної геометрії німецький математик К. Клавій (1574), італійські математики П. Катальді (вперше в 1603 надрукував роботу, повністю присвячену питанню паралельних прямих), Дж. Бореллі (1658), Дж. Вітале (1680), англійський математик Джон Волліс (1663, опубліковано в 1693) (Уолліс грунтує доведення V постулату на припущенні, що для кожної фігури існує подібна їй, але не рівна фігура). Доведення вказаних вчених зводились до заміни V постулату іншими припущеннями, що здавались більш очевидними. Дж. Бореллі

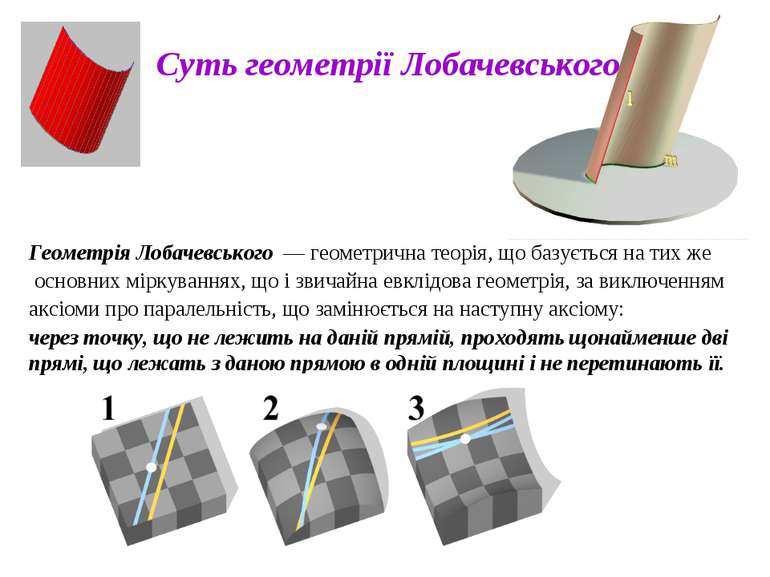
Суть геометрії Лобачевського Лобачевський розв'язав задачу, яку протягом більш як двох тисяч років марно намагалися розв'язати багато видатних учених-математиків: він довів, що V постулат Евкліда не можна дістати як теорему з інших постулатів і аксіом, які містяться в «Началах» Евкліда. Він довів також, що Евклідова геометрія не є єдино можливою геометрією. Це спростовувало ідею німецького професора Канта про те, що людина народжується з уявленням про зовнішній світ, де діє лише Евклідова геометрія.

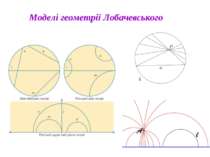
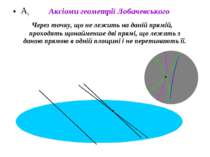
Суть геометрії Лобачевського Геометрія Лобачевського — геометрична теорія, що базується на тих же основних міркуваннях, що і звичайна евклідова геометрія, за виключенням аксіоми про паралельність, що замінюється на наступну аксіому: через точку, що не лежить на даній прямій, проходять щонайменше дві прямі, що лежать з даною прямою в одній площині і не перетинають її.

Моделі геометрії Лобачевського

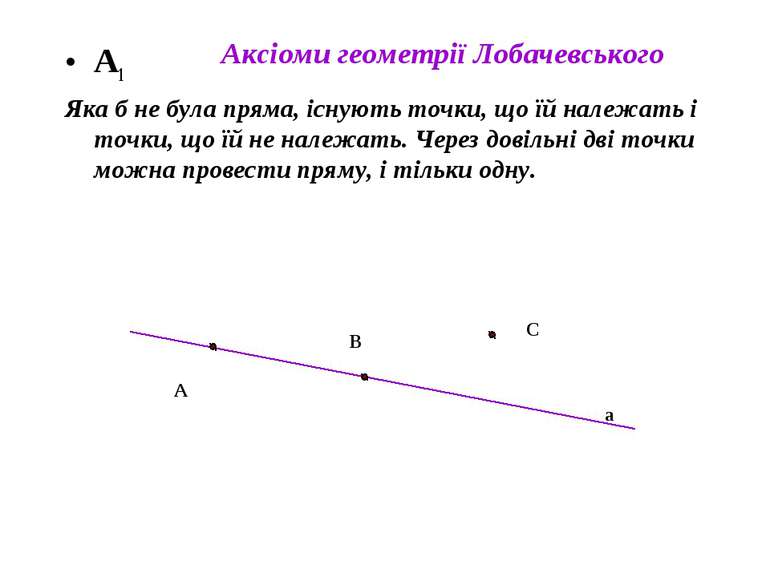
А1 Яка б не була пряма, існують точки, що їй належать і точки, що їй не належать. Через довільні дві точки можна провести пряму, і тільки одну. A В С a Аксіоми геометрії Лобачевського

А2 З трьох точок на прямій одна і тільки одна лежить між двома іншими. A В С a Аксіоми геометрії Лобачевського

А3 Будь який відрізок має певну довжину, більшу 0. Довжина відрізка дорівнює сумі довжин його частин, на які він розбивається будь-якою його точкою. A В С Аксіоми геометрії Лобачевського

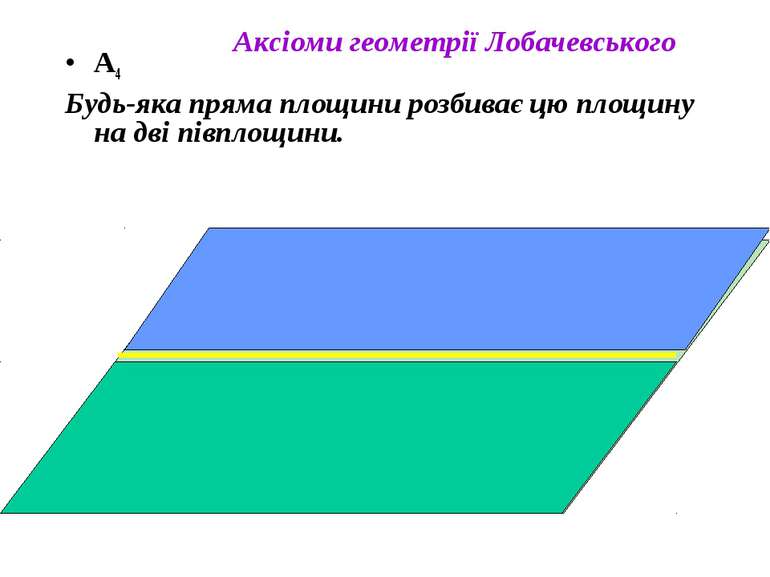
А4 Будь-яка пряма площини розбиває цю площину на дві півплощини. Аксіоми геометрії Лобачевського

А5 Будь-який кут має градусну міру більшу 0. Розгорнутий кут дорівнює 1800. С В О Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що виходить з вершини кута і проходить між його сторонами. А Аксіоми геометрії Лобачевського

А6 На будь-якому промені від його початкової точки можна відкласти відрізок заданої довжини, і тільки один. A В С Аксіоми геометрії Лобачевського

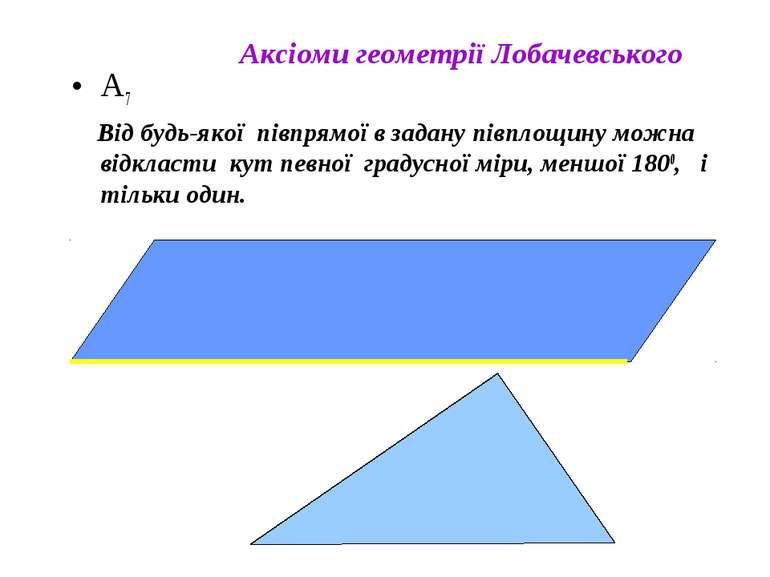
А7 Від будь-якої півпрямої в задану півплощину можна відкласти кут певної градусної міри, меншої 1800, і тільки один. Аксіоми геометрії Лобачевського

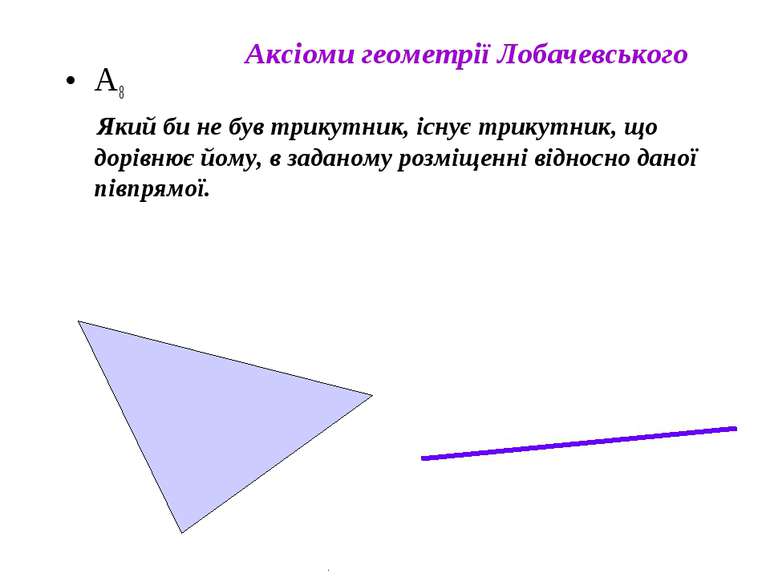
А8 Який би не був трикутник, існує трикутник, що дорівнює йому, в заданому розміщенні відносно даної півпрямої. Аксіоми геометрії Лобачевського

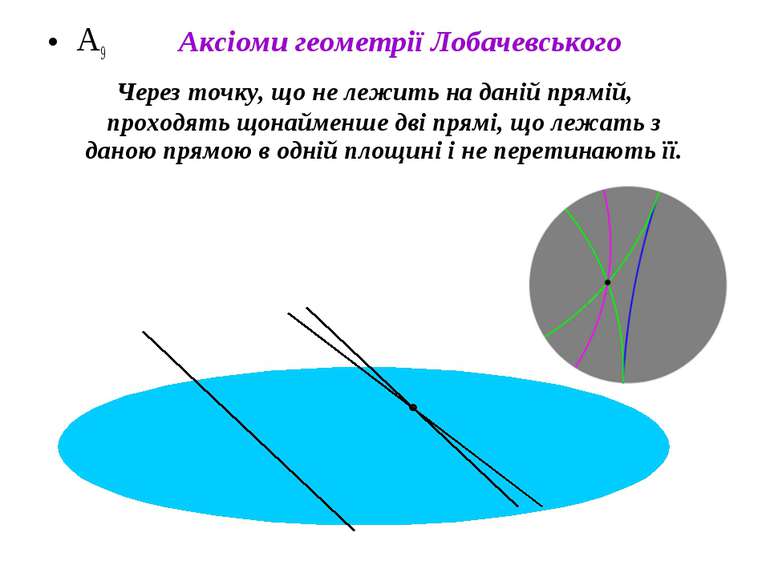
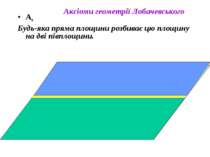
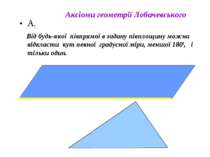
А9 Через точку, що не лежить на даній прямій, проходять щонайменше дві прямі, що лежать з даною прямою в одній площині і не перетинають її. Аксіоми геометрії Лобачевського

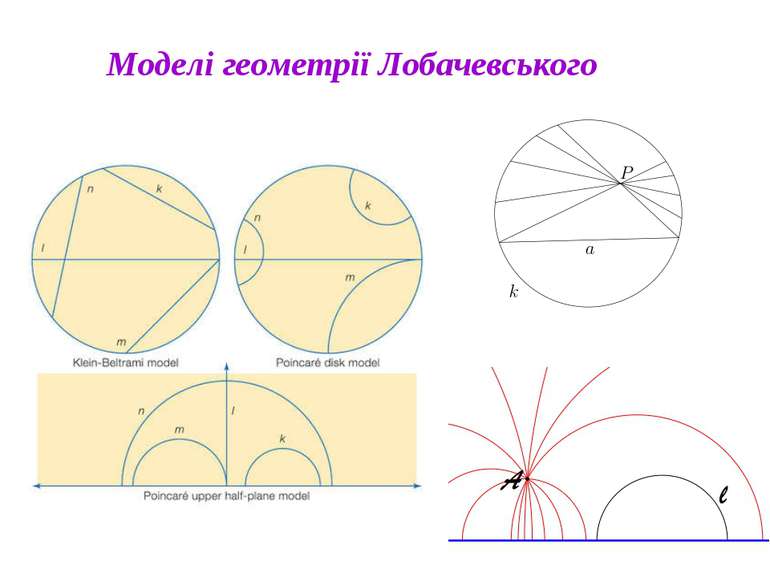
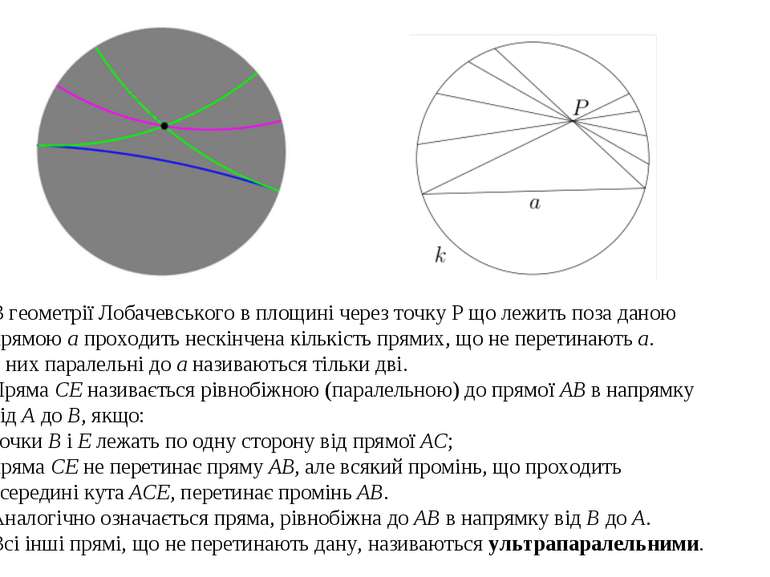
В геометрії Лобачевського в площині через точку Р що лежить поза даною прямою а проходить нескінчена кількість прямих, що не перетинають а. З них паралельні до а називаються тільки дві. Пряма CE називається рівнобіжною (паралельною) до прямої AB в напрямку від A до B, якщо: точки B і E лежать по одну сторону від прямої AC; пряма CE не перетинає пряму AB, але всякий промінь, що проходить всередині кута ACE, перетинає промінь AB. Аналогічно означається пряма, рівнобіжна до AB в напрямку від B до A. Всі інші прямі, що не перетинають дану, називаються ультрапаралельними.

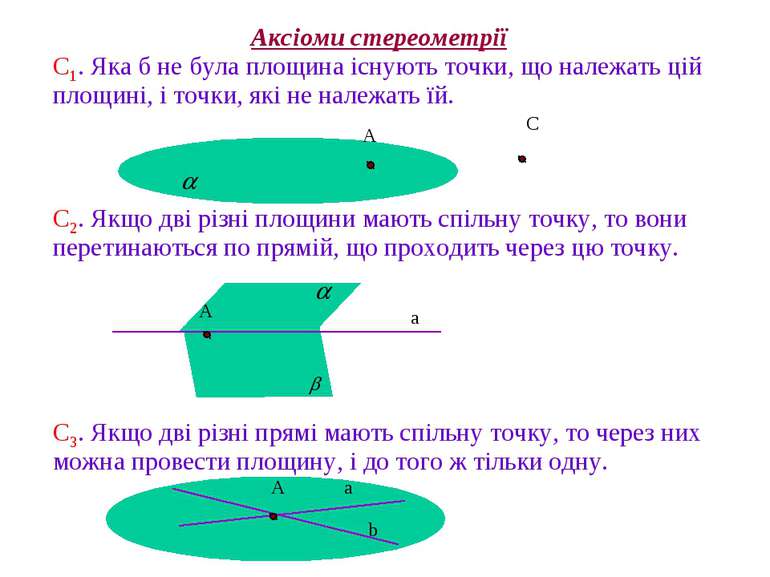
С1. Яка б не була площина існують точки, що належать цій площині, і точки, які не належать їй. С2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку. С3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну. Аксіоми стереометрії A C a A A a b