Презентація на тему:
Многокутник

Правильні многокутники

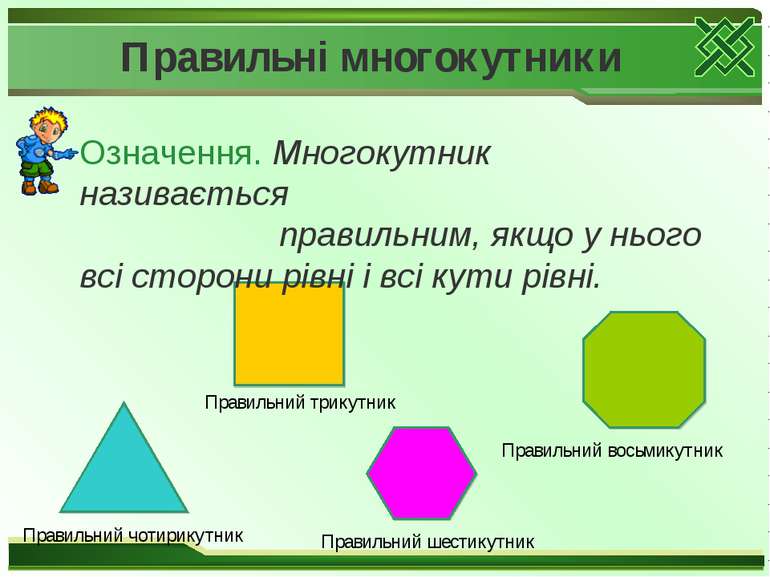
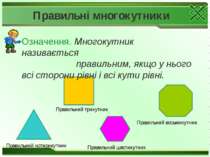
Правильні многокутники Означення. Многокутник називається правильним, якщо у нього всі сторони рівні і всі кути рівні. Правильний восьмикутник Правильний шестикутник Правильний трикутник Правильний чотирикутник

Правильні многокутники Які з поданих фігур є правильними многокутниками

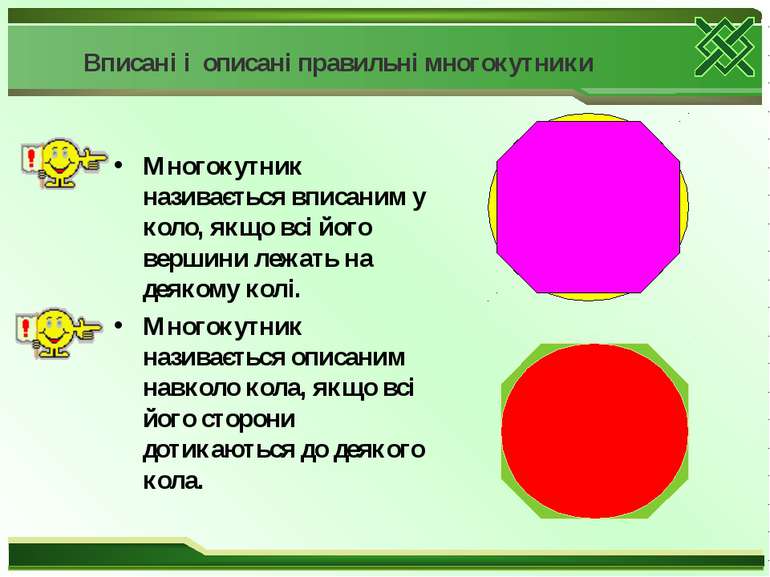
Вписані і описані правильні многокутники Многокутник називається вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до деякого кола.

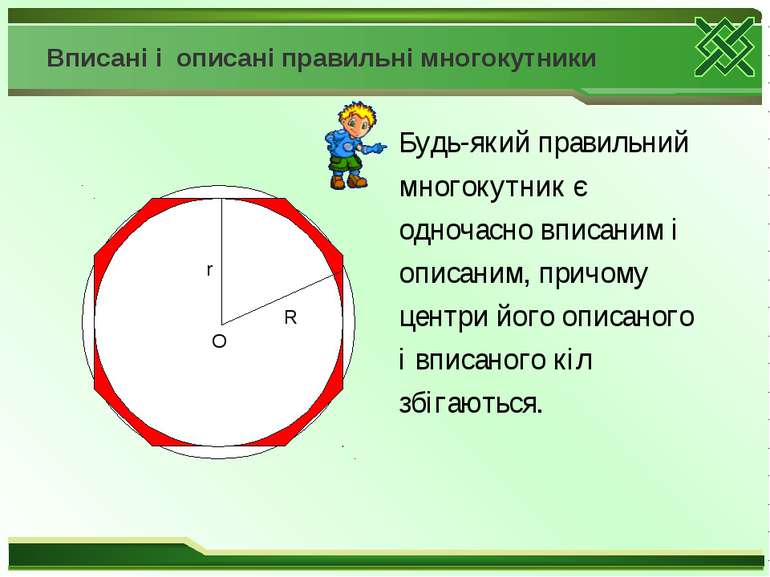
Вписані і описані правильні многокутники Будь-який правильний многокутник є одночасно вписаним і описаним, причому центри його описаного і вписаного кіл збігаються. R r О

Формули для радіусів вписаних і описаних кіл правильних многокутників

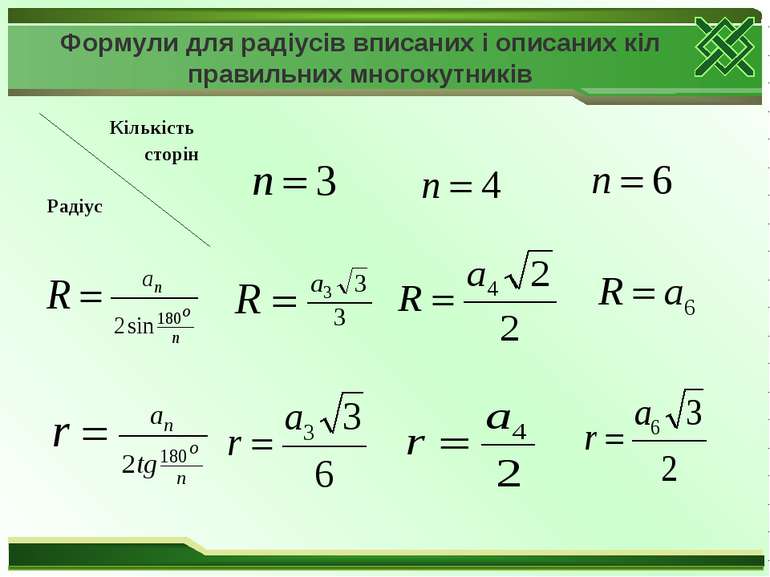
Задача Виразіть сторону правильного n-кутника через радіус R описаного навколо нього і радіус r вписаного в нього кола. Обчисліть , якщо n=3,4,6.

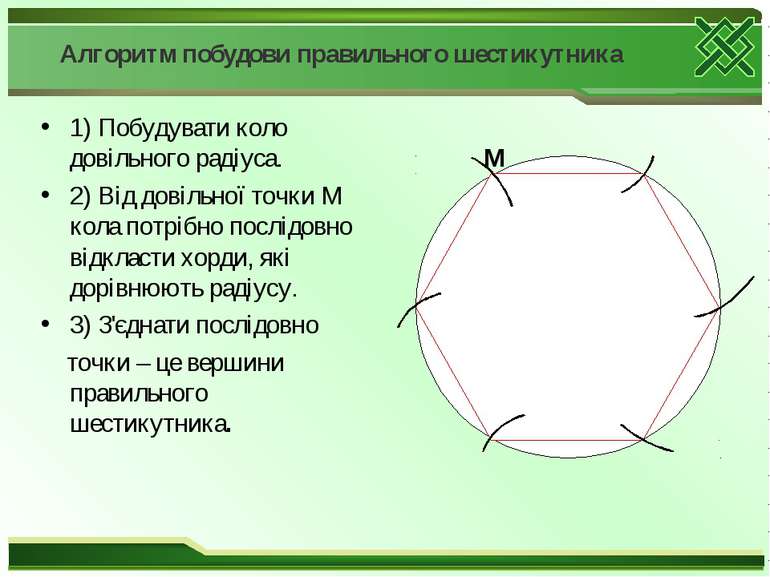
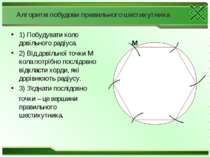
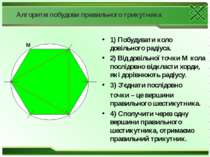
Алгоритм побудови правильного шестикутника 1) Побудувати коло довільного радіуса. 2) Від довільної точки М кола потрібно послідовно відкласти хорди, які дорівнюють радіусу. 3) З'єднати послідовно точки – це вершини правильного шестикутника. М

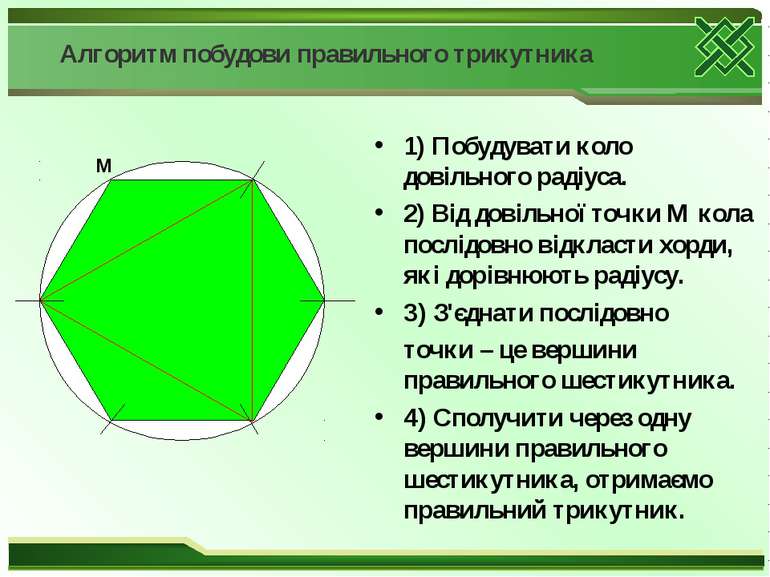
Алгоритм побудови правильного трикутника 1) Побудувати коло довільного радіуса. 2) Від довільної точки М кола послідовно відкласти хорди, які дорівнюють радіусу. 3) З'єднати послідовно точки – це вершини правильного шестикутника. 4) Сполучити через одну вершини правильного шестикутника, отримаємо правильний трикутник. М

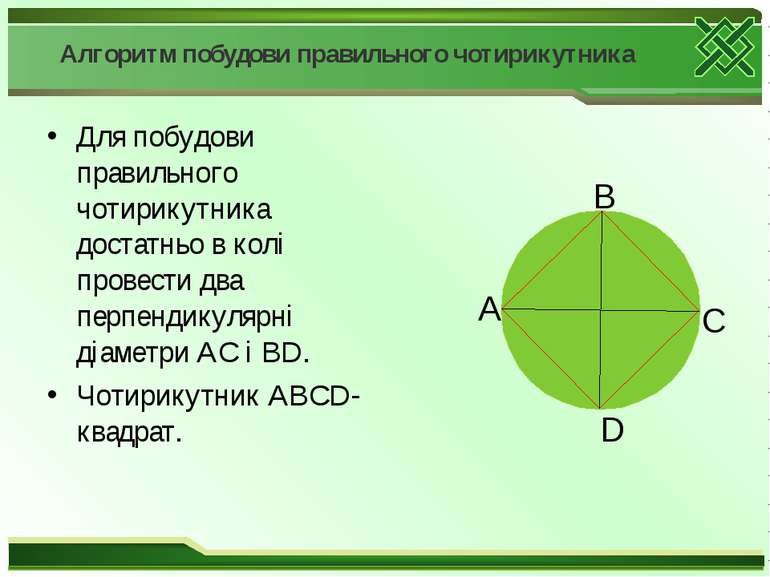
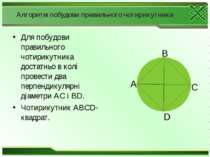
Алгоритм побудови правильного чотирикутника Для побудови правильного чотирикутника достатньо в колі провести два перпендикулярні діаметри АС і ВD. Чотирикутник АВСD- квадрат. C A D B

Стародавні вчені, які вміли будувати будь-який із правильних n-кутників, де n=3,4,5,6.8,10,намагалися розв'язати цю задачу і для n=7,9. Їм це не вдалося. І лише у кінці XVIII ст. 19-річний студент Геттінгенського університету, в майбутньому видатний німецький математик Карл Фрідріх Гаусс повністю розв'язав питання про побудову правильних многокутників циркулем і лінійкою – це було його перше відкриття. Він довів, що за допомогою циркуля і лінійки можна побудувати правильний 17-кутник. Взагалі він довів, що поділити коло на n рівних частин, або, що те саме, побудувати правильний n-кутник, за допомогою циркуля і лінійки можна лише тоді, коли n є просте число виду n= , де k- ціле додатне число або нуль, наприклад: n=3,5,17,257,65537. При цьому очевидно, що коли побудовано правильний n-кутник, то легко побудувати і правильний 2n-кутник. Гаусс дуже пишався своїм першим відкриттям, і рисунок правильного сімнадцятикутника звелів викарбувати на своїй могильній плиті.

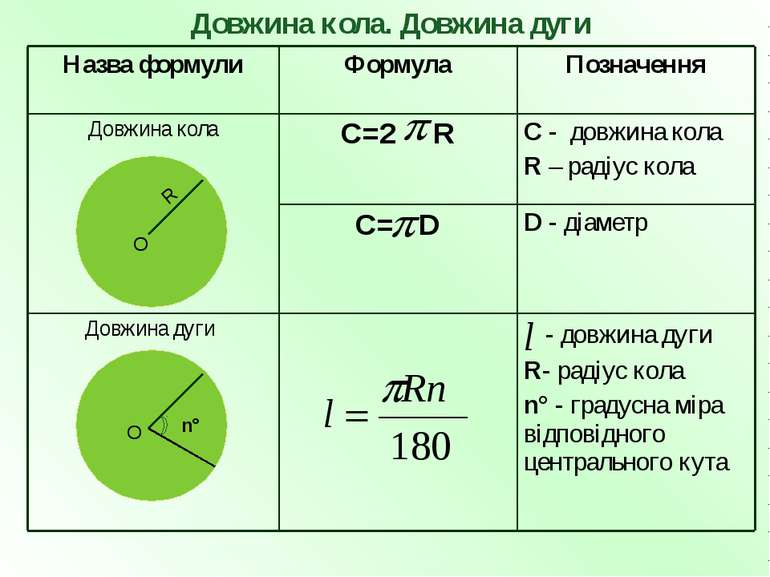
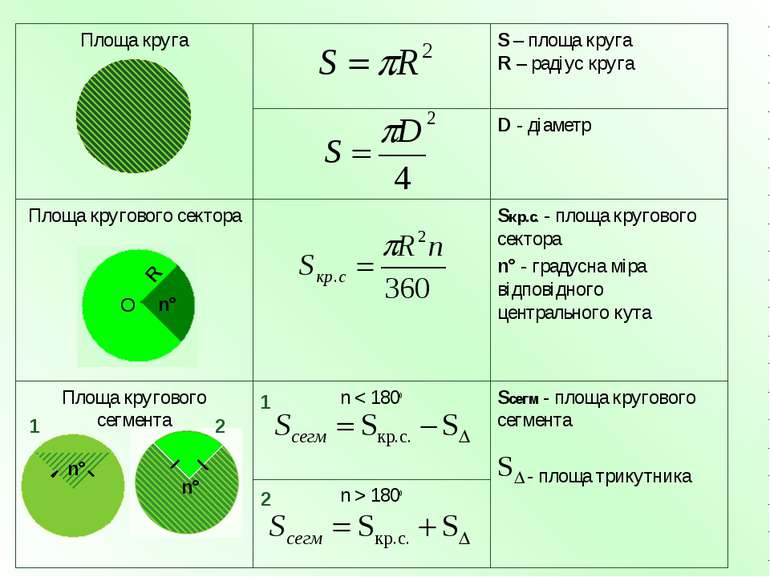
- довжина дуги R- радіус кола n° - градусна міра відповідного центрального кута Довжина дуги D - діаметр C= D C - довжина кола R – радіус кола С=2 R Довжина кола Позначення Формула Назва формули Довжина кола. Довжина дуги

n > 180o Sсегм - площа кругового сегмента - площа трикутника n < 180o Площа кругового сегмента Sкр.с. - площа кругового сектора n° - градусна міра відповідного центрального кута Площа кругового сектора D - діаметр S – площа круга R – радіус круга Площа круга О R n° 1 2 1 2 n° n°

Задача У дворі нашої школи є клумба квадратної форми. Навесні ми будемо садити квіти на нашу клумбу. Спочатку ми будемо садити конвалії по колу, яке можна вписати в квадратну клумбу. Потім тюльпани - в формі квадрата, який вписаний в коло. Скільки саджанців конвалій і цибулин тюльпанів потрібно посадити, якщо розміри клумби 6х6 квадратних метрів? Садити квіти потрібно через кожні 20 см.

Розв’язання Оскільки коло вписане в квадрат, то радіус кола дорівнює половині сторони квадрата. Знайдемо кількість конвалій, потрібних для посадки. 19:0,2=95( шт ) Сторона вписаного квадрата буде дорівнювати м. Периметр цього квадрата дорівнює Обчислимо кількість цибулин тюльпанів, необхідних для посадки 16,8 : 0,2 = 84 (шт) Відповідь: 95 конвалій; 84 цибулини тюльпанів

Задача В кондитерському цеху зробили круглий торт радіусом 18 см. Для пакування є два види коробок: квадратної форми і форми правильного шестикутника. В яку коробку помістимо торт, якщо сторона квадратної коробки 36 см, а шестикутної – 20 см ?

Розв’язання Оскільки радіус торта дорівнює 18 см, то для розв’язання задачі потрібно перевірити радіуси вписаних кіл для двох видів коробок. Сторона квадратної коробки дорівнює 36 см, отже, радіус вписаного кола дорівнює 18 см. Таким чином, торт поміститься в квадратну коробку. Перевіримо другу коробку. Трикутник АОВ прямокутний, О B A

За співвідношеннями між сторонами і кутами прямокутного трикутника маємо: : Сторона коробки дорівнює Порівняємо сторони обох коробок. Таким чином, торт не поміститься в коробку форми правильного шестикутника.

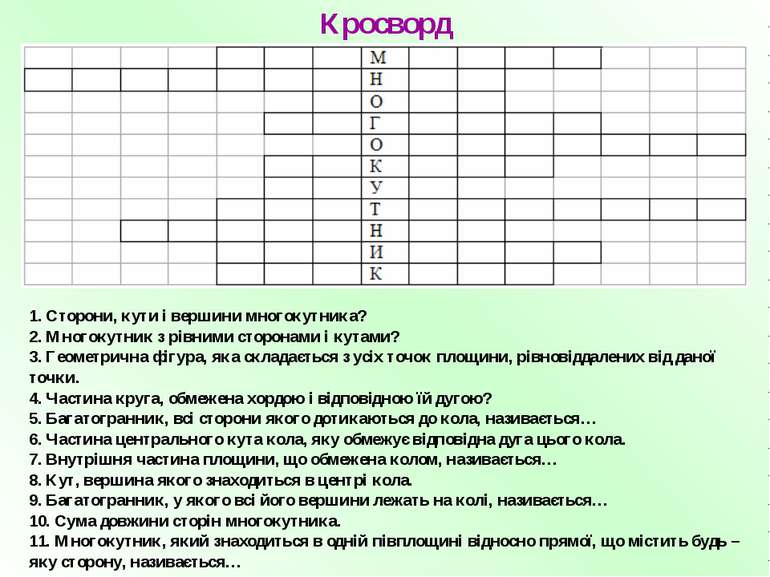
1. Сторони, кути і вершини многокутника? 2. Многокутник з рівними сторонами і кутами? 3. Геометрична фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. 4. Частина круга, обмежена хордою і відповідною їй дугою? 5. Багатогранник, всі сторони якого дотикаються до кола, називається… 6. Частина центрального кута кола, яку обмежує відповідна дуга цього кола. 7. Внутрішня частина площини, що обмежена колом, називається… 8. Кут, вершина якого знаходиться в центрі кола. 9. Багатогранник, у якого всі його вершини лежать на колі, називається… 10. Сума довжини сторін многокутника. 11. Многокутник, який знаходиться в одній півплощині відносно прямої, що містить будь – яку сторону, називається… Кросворд

Список використаних джерел Апостолова Г.В. Геометрія: 9: дворівн. підруч. для загальноосвіт. навч. закл./ Г.В. Апостолова. – К. : Генеза, 2009. – 304с. : іл. О.С. Істер, Збірник завдань для державної підсумкової атестації з математики: 9кл./ О.С. Істер, О.І. Глобін, О.В. Комаренко.- К.: Центр навч.- метод. л-ри, 2011.-112с.:іл. Мерзляк А.Г., Полонський В.Б., Якір М.С. Геометрія: Підруч. для 9 кл. шкіл з поглибл. вивченням математики.- Х.:Гімназія, 2009.-272с.: іл. О.Г. Черватюк, Г.Д. Шиманська, Елементи цікавої математики на уроках математики, видавництво “Радянська школа”, Київ – 1968. -188с. http://dpravda.org/ http://www.topledi.com/ http://www.guolit.com/ http://stroimat.com.ua/