Презентація на тему:
Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб
Завантажити презентацію
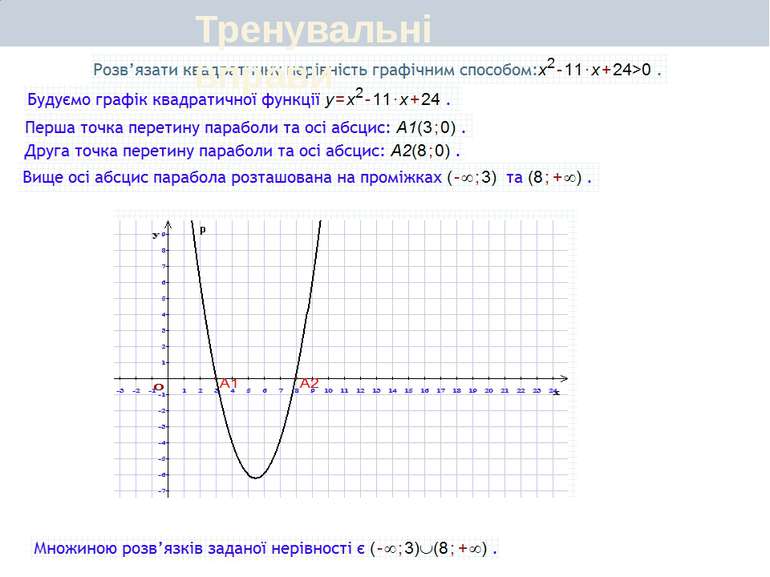
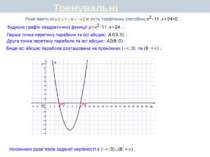
Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб
Завантажити презентаціюПрезентація по слайдам:
Тема 4 Квадратні нерівності та системи рівнянь другого степеня Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб. Розв’язування нерівностей другого степеня з однією змінною. Аналітичний спосіб Метод інтервалів Степінь рівняння з двома змінними. Розв’язування систем рівнянь з двома змінними Розв’язування вправ. Самостійна робота Розв’язування текстових задач складанням систем рівнянь з двома змінними
Пункт 5.1. Пригадайте: Що таке квадратний тричлен? На проміжку (а; b) значення функції є додатними. Як розміщені точки графіка цієї функції на даному проміжку відносно осі Ох? Як за графіком функції встановити числові проміжки, де вона набуває від'ємних значень? Де розміщені точки графіка функції, в яких її значення дорівнюють нулю? Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб.
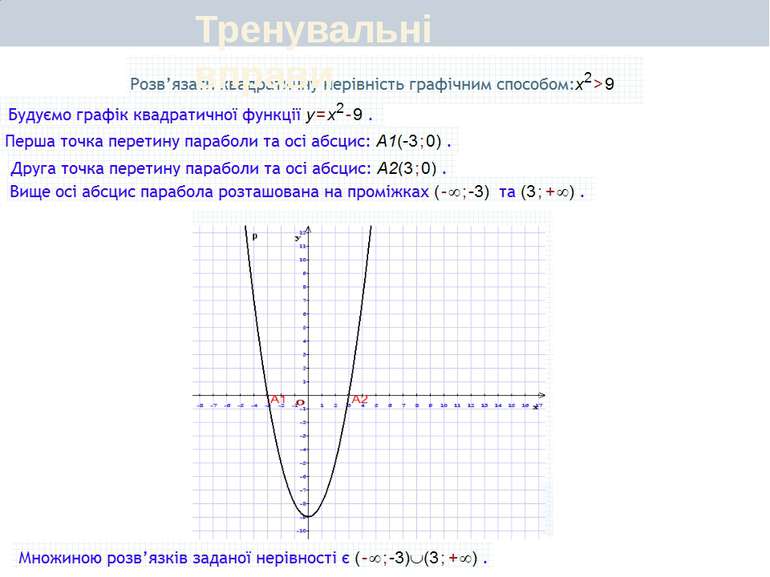
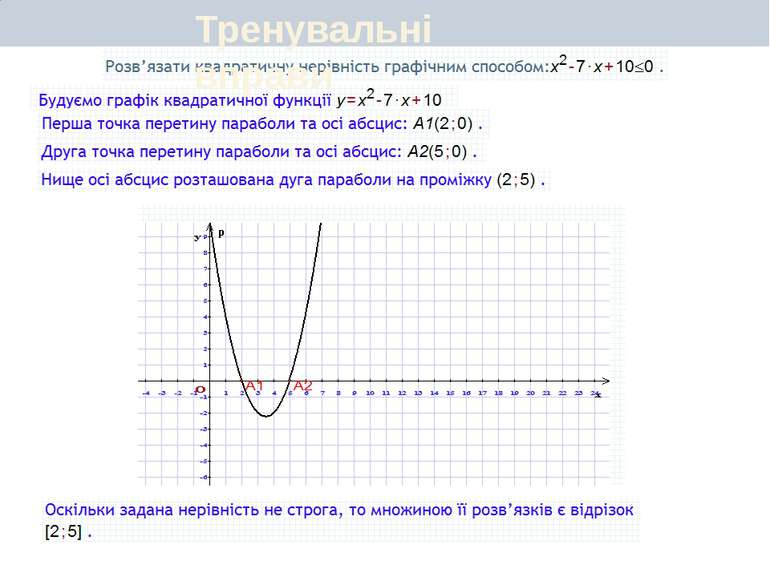
Первинне закріплення вивченого матеріалу Тренувальні вправи Запитання для самоперевірки У чому суть графічного способу розв'язування нерівностей другого степеня з однією змінною? Скільки розв'язків може мати квадратна нерівність? Наведіть відповідні графічні ілюстрації.
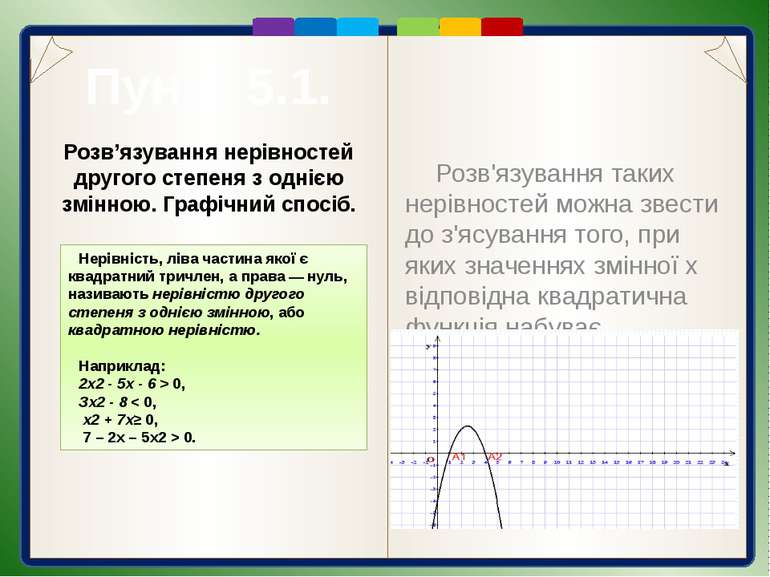
Пункт 5.1. Розв'язування таких нерівностей можна звести до з'ясування того, при яких значеннях змінної х відповідна квадратична функція набуває додатного (невід'ємного) або від'ємного (недодатного) значення. Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб. Нерівність, ліва частина якої є квадратний тричлен, а права — нуль, називають нерівністю другого степеня з однією змінною, або квадратною нерівністю. Наприклад: 2х2 - 5х - 6 > 0, Зх2 - 8 < 0, х2 + 7х≥ 0, 7 – 2х – 5х2 > 0.
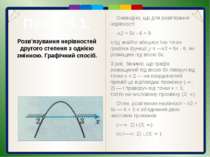
Пункт 5.1. Щоб розв'язати нерівність другого степеня, досить знати спрямування гілок відповідної параболи і наявність у неї спільних точок з віссю Ох, тобто точок, у яких значення даної функції дорівнюють нулю (нулі функції). Наприклад, гілки параболи у = —х2 + 5х - 6 спрямовані вниз. Для знаходження нулів цієї функції розв'яжемо рівняння -х2 + 5х - 6 = 0. Маємо: х1 = 2, х2 = 3. Отже, графік функції у = —х2 + 5х - 6 розміщений відносно осі Ох так, як зображено на рисунку. Додатні значення функції — це значення ординат тих точок її графіка, що лежать над віссю Ох (відповідну частину графіка виділено на рисунку жирною лінією). Абсциси усіх цих точок належать проміжку (2; 3). Отже, розв'язком нерівності —х2 + 5х — 6 > 0 є проміжок (2; 3): х (2; 3). Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб.
Пункт 5.1. Очевидно, що для розв'язання нерівності -х2 + 5х - 6 < 0 слід знайти абсциси тих точок графіка функції у = —х2 + 5х - 6, які розміщені під віссю 0х. З рис. бачимо, що графік розміщений під віссю 0х ліворуч від точки х = 2 — на координатній прямій це відповідає проміжку (-∞; 2) — і праворуч від точки х = З, тобто на числовому проміжку (3; ∞). Отже, розв'язком нерівності - х2 + 5х — 6 < 0 є об'єднання двох числових проміжків (—∞; 2) і (3; ∞): х (—∞; 2) (3; ∞ ). Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб.
Пункт 5.1. Якщо схематичне зображення розміщення графіка функції у = ах2 + bх + с відносно осі 0x має вигляд, як на рис., то очевидно, що при всіх дійсних значеннях х ця функція набуває додатних значень. У такому випадку розв'язком нерівності ах2 + bх + с > 0 буде множина всіх дійсних чисел, тобто числовий проміжок (-∞; ∞), а нерівність ах2 + bх + с < 0 не матиме розв'язків. Приклади розв’язування квадратних нерівностей Графічний спосіб.
Пункт 5.1. Розв'язання. Для спрощення розв'язання замінимо дану нерівність рівносильною нерівністю, помноживши обидві її частини на -1. Маємо: Зх2 + 5х + 2 > 0. Знайдемо корені рівняння Зх2 + 5х + 2 = 0. D = 25-24= 1; Побудуємо схематичне зображення розміщення графіка функції у = Зх2 + 5х + 2 відносно осі Ох. Знайдемо значення х, при яких гілки параболи розміщені над віссю Ох (Зx2 + 5х + 2 > 0). З рисунка видно, що це ті значення, що знаходяться на координатній прямій ліворуч від точки х = —1 (числовий проміжок (-∞; —1)), а також праворуч від точки х=-2/3 (числовий проміжок (-2/3; ∞ ). Відповідь, х є (-∞; -1) U (-2/3;∞) Приклади розв’язування квадратних нерівностей Графічний спосіб. Приклад 1. Розв'язати нерівність: — Зх2 — 5х — 2 < 0.
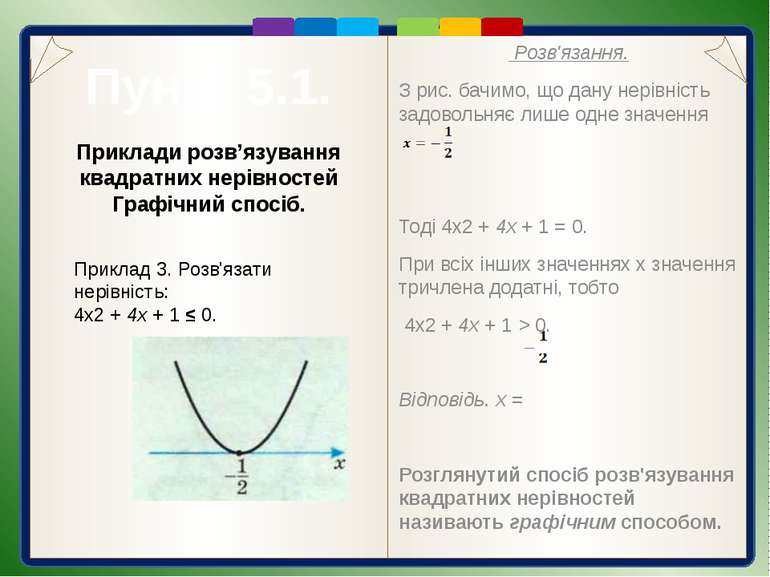
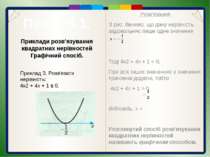
Пункт 5.1. Розв'язання. Знайдемо корені тричлена 4х2 + 4х + 1, тобто нулі функції у = 4х2 + 4х+ 1. 4х2 + 4х + 1 = 0; (2x+ 1)2 = 0; Побудуємо схематичне зображення графіка цієї функції відносно осі 0х. Бачимо, що над віссю 0x (4x2 + 4х + 1 > 0) розміщені всі точки параболи, крім однієї —з абсцисою . Отже, розв'язком даної нерівності є всі дійсні числа, крім . Відповідь. Приклади розв’язування квадратних нерівностей Графічний спосіб. Приклад 2. Розв'язати нерівність: 4х2 + 4х + 1 > 0.
Пункт 5.1. Розв'язання. З рис. бачимо, що дану нерівність задовольняє лише одне значення Тоді 4х2 + 4х + 1 = 0. При всіх інших значеннях х значення тричлена додатні, тобто 4х2 + 4х + 1 > 0. Відповідь. х = Розглянутий спосіб розв'язування квадратних нерівностей називають графічним способом. Приклади розв’язування квадратних нерівностей Графічний спосіб. Приклад 3. Розв'язати нерівність: 4х2 + 4х + 1 ≤ 0.
Схожі презентації
Категорії