Презентація на тему:
Координатно-параметричний метод розв`язування рівнянь і нерівностей. (Факультатив)

Вчитель: Шушпанова Т. М.

а а х х 0 0 або 0х – координатна числова вісь 0а – параметрична вісь (х0а) або (а0х) – КП площина

КП – метод заснований на знаходженні множини всіх точок КП – площини, де значення координат Х і параметра а задовольняють заданій в умовах завдання співвідношенню F(х;а)=0

При запису відповіді поставимо у відповідність кожному допустимому фіксованому значенню параметра а значення шуканої величини Х – координати відповідних точок знайденої множини.

Будь-яке рівняння чи нерівність з параметрами розв’язують як звичайні рівняння чи нерівність доти, поки всі перетворення або міркування, необхідні для розв’язування, можна виконати однозначно. Буває зручно супроводжувати відповідні міркування схемами. Зазначимо, що рівняння та нерівності з параметрами найчастіше розв’язують за допомогою їх рівносильних перетворень, хоча інколи використовують: властивості функцій, метод інтервалів (для розв ’язування нерівностей) ,рівняння – наслідки, рівносильні перетворення. Орієнтиром при розв’язуванні завдань з параметрами є:

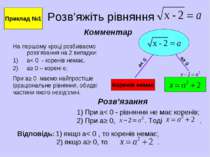
Розв’яжіть рівняння На першому кроці розбиваємо розв’язання на 2 випадки: a< 0 - коренів немає, a≥ 0 – корені є; Приклад №1 При a≥ 0 маємо найпростіше ірраціональне рівняння, обидві частини якого невід’ємні. Розв’язання 1) При a< 0 - рівняння не має коренів; 2) При a≥ 0, . Тоді . Комментар

Розв`яжіть рівняння Для всіх коренів даного рівняння х≥0. (1) Тоді задане рівняння рівносильне рівнянням: (2) (3) Для всіх коренів рівняння (4) Тоді рівняння (3) рівносильне рівнянням: (5) (6) Розглянемо рівняння (6) як квадратне відносно а: D= Тоді а= Отже, а= або а= Звідси (7) Або (8) Ураховуючи умови (1) і (4), одержимо, що , Отже, рівняння (7) не має коренів. Приклад №2 Комментар ОДЗ данного рівняння є ОДЗ буде враховано при переході до рівнянь (2) та (5). Для (2),(3),(5),(6) повністю аналогічне міркування до прикладу (2) Аналізуючи рівняння (6), користуємося орієнтиром, а саме: спробуйте розглянути задане рівняння як квадратне відносно якоїсь змінної(чи функції). У даному випадку розглянемо це рівняння як квадратне відносно параметра a. * Цей спосіб ефективний тільки тоді, коли дискримінант одержаного квадратного тричлена є повним квадратом, як у розглянутого випадку. Розв`язок

Якщо для коренів рівняння (8) виконується умова (1) (х≥ 0), то автоматично виконується й умова (4) ( ). Із рівняння (8) одержимо: Це рівняння має корені, якщо D=1+4а ≥0, тобто при а ≥- Тоді , Для умова х ≥0, виконується, Отже, - корінь заданого рівняння при а ≥- Урахуємо умову х ≥ 0 для : ≥ 0, , , . Відповідь: При 2) При a>0 х= ; 3)При а0 у відповідь потрібно записати тільки одну формулу( ), при дві формули ( і ), а при a

Розв`яжіть нерівність Із теорії відомо: або Якщо в одержані системи параметр а входить лінійно, то в таких випадках іноді буває зручно виразити параметр через змінну, розглянути параметр як функцію від цієї змінної і використати графічну ілюстрацію розв`язування нерівностей (у системі координат хОа) для зображення розв`язків сукупності нерівностей зручно використовувати дві системи координат, у яких осі Ох розташовані на одній прямій, І на кожній виділять штриховкою відповідні розв`язки.При різних значеннях а пряма а=const або не перетинає заштриховані області (при а ), або перетинає їх по відрізках. Абсциси точок перетину є розв`язками систем (1)і (2), а отже, і розв`язками заданої нерівності. Приклад №3

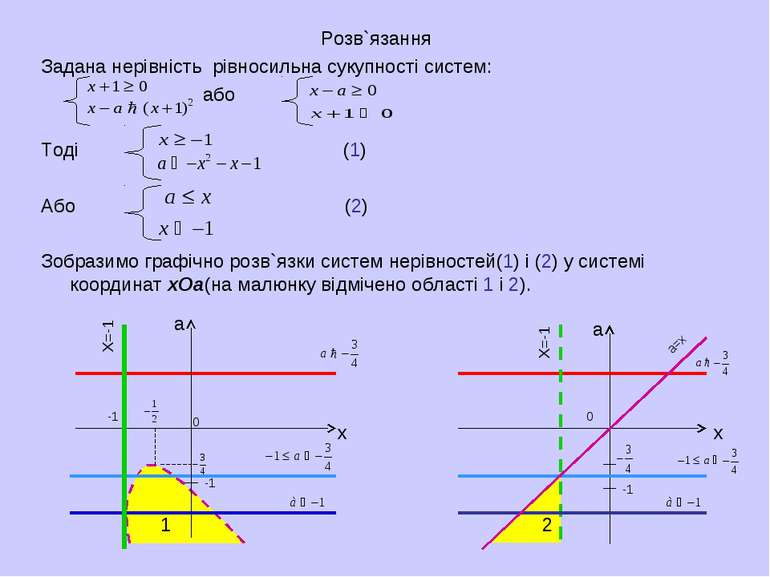
Розв`язання Задана нерівність рівносильна сукупності систем: або Тоді (1) Або (2) Зобразимо графічно розв`язки систем нерівностей(1) і (2) у системі координат хОа(на малюнку відмічено області 1 і 2).

За малюнками ми бачимо, що при а розв`язків немає(немає зафарбованих точок); якщо , то пряма а=const перетинає тільки заштриховану область 1 Причому одержаний інтервал обмежений зліва і справа вітками параболи а= . Але для відповіді нам потрібно записати х через а. Для цього з рівняння знаходимо х: Як бачимо, ,тобто - рівняння правої вітки параболи, а - лівої. Тоді відповідь у цьому випадку буде такою : Якщо a

Для області 2 інтервал для х обмежений зліва прямою х=а, а справа – прямою х=-1, тобто Об`єднання цих інтервалів можна коротше записати так : Відповідь: При - розв`язків немає; При - ; При а