Презентація на тему:
Розв’язування квадратичних нерівностей

Розв’язування квадратичних нерівностей

Зміст ax2+bx+c≤0, a>0 ax2+bx+c≥0, a>0 ax2+bx+c0 ax2+bx+c>0, a>0 ax2+bx+c≤0, a

Розглянемо та запишемо алгоритм розв’язування нерівності ax2+bx+c≤0, a>0 графічним способом

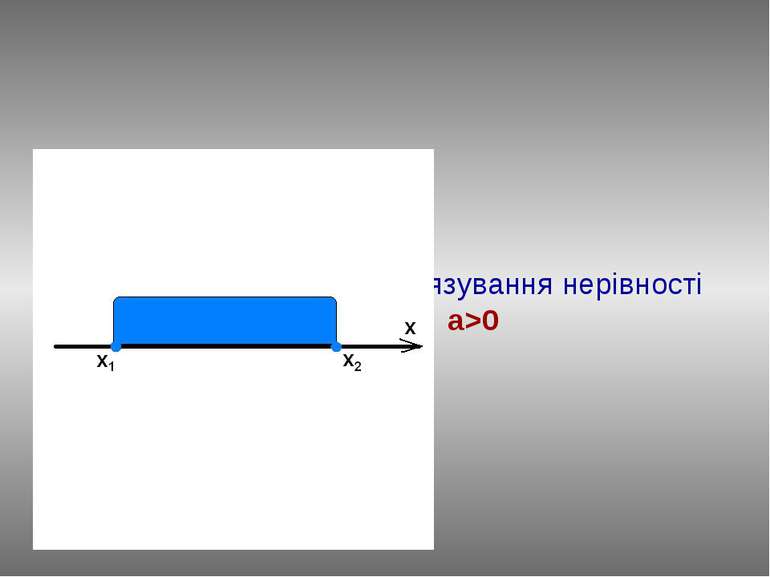
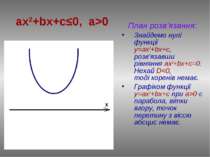
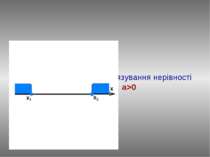
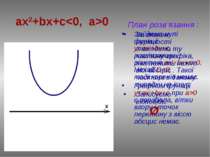
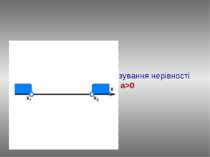
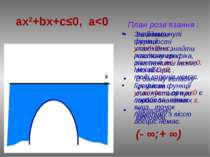
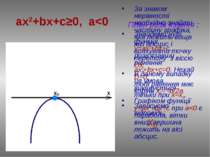
ax2+bx+c≤0, a>0 План розв’язання: Знаходимо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D>0, тоді у(х1)=0, у(х2)=0. Відмітимо числа х1 и х2 на вісі абсцис. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а (х1;0) та (х2;0) точки перетину з віссю ОХ. За знаком нерівності виділяємо ту частину графіка, яка лежить нижче вісі абсцис і враховуємо точки перетину з віссю. Визначаємо проміжок, на якому виділили частину графіка. Записуємо відповідь: [х1 ; х2]

Повторимо алгоритм розв’язування нерівності ax2+bx+c≤0, a>0

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

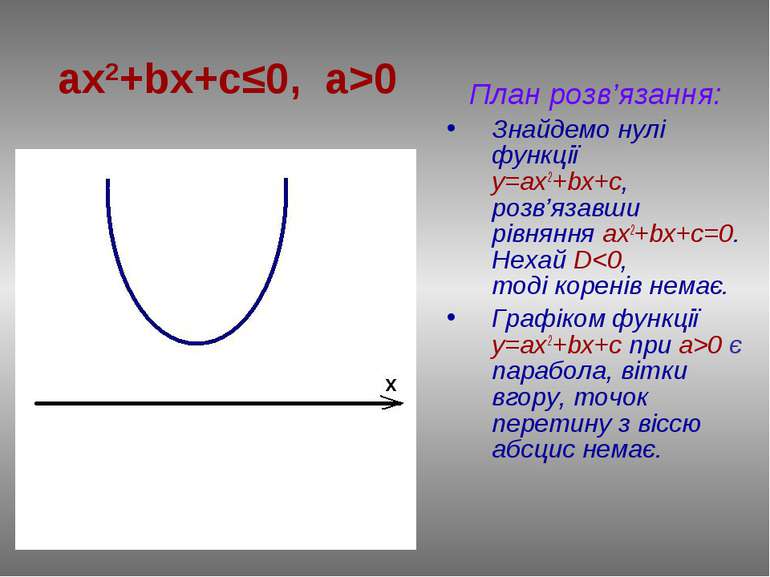
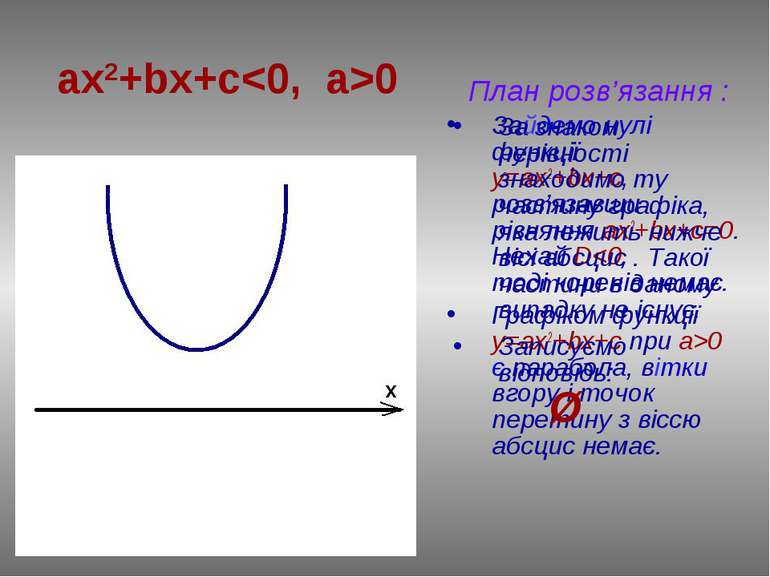
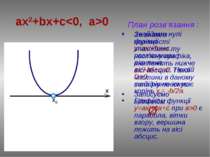
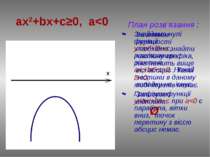
План розв’язання: Знайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D0 є парабола, вітки вгору, точок перетину з віссю абсцис немає. ax2+bx+c≤0, a>0

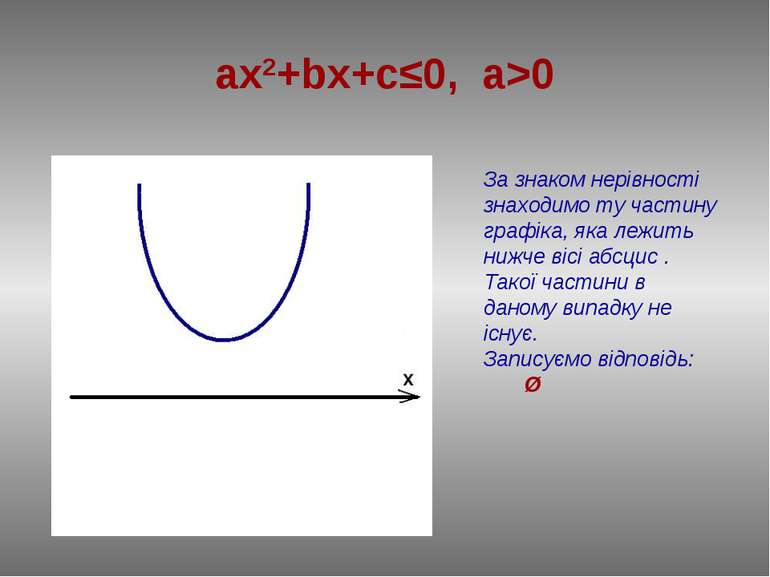
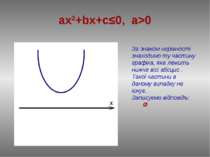
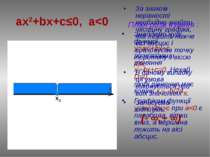
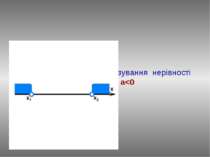
ax2+bx+c≤0, a>0 За знаком нерівності знаходимо ту частину графіка, яка лежить нижче вісі абсцис . Такої частини в даному випадку не існує. Записуємо відповідь: Ø

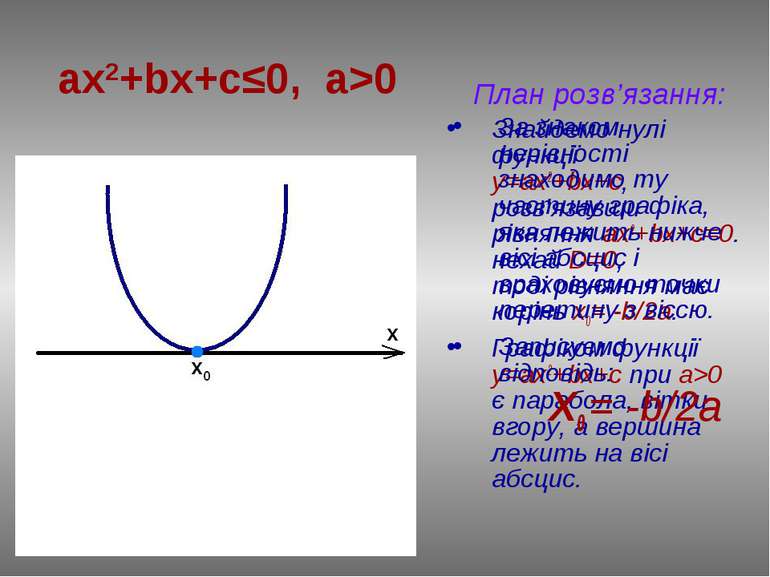
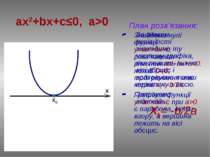
План розв’язання: Знайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а вершина лежить на вісі абсцис. ax2+bx+c≤0, a>0 За знаком нерівності знаходимо ту частину графіка, яка лежить нижче вісі абсцис і враховуємо точки перетину з віссю. Записуємо відповідь: Х0 = -b/2a

Розглянемо та запишемо алгоритм розв’язування нерівності ax2+bx+c≥0, a>0 графічним способом

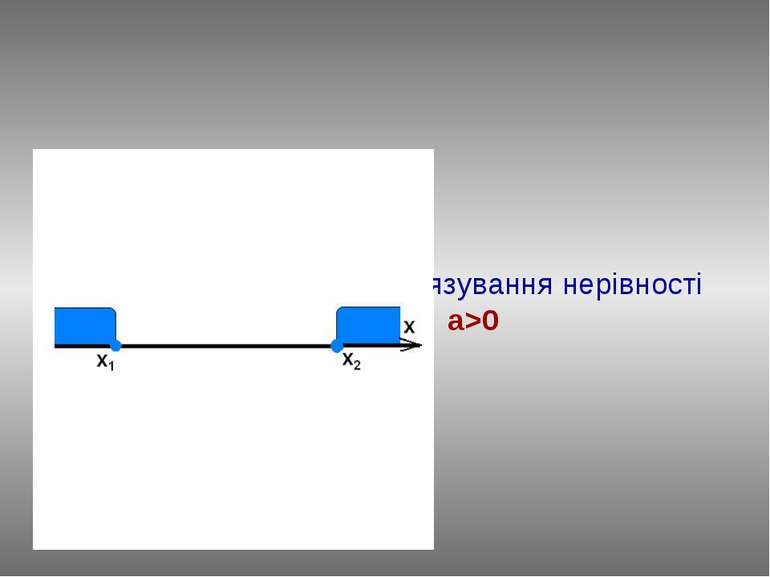
План розв’язання: Знайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D>0, тоді у(х1)=0, у(х2)=0. Відмітимо числа х1 и х2 на вісі абсцис. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а (х1;0) та (х2;0) точки перетину з віссю ОХ. ax2+bx+c≥0, a>0 За знаком нерівності виділяємо ті частини графіка, які лежать вище вісі абсцис і враховуємо точки перетину з віссю. Визначаємо проміжки, на яких виділили частини графіка. Записуємо відповідь: (-∞;х1 ]U[х2;+∞)

Повторимо алгоритм розв’язування нерівності ax2+bx+c≥0, a>0

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

План розв’язання: Знайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D0 є парабола, вітки вгору, точок перетину з віссю абсцис немає. ax2+bx+c≥0, a>0 За знаком нерівності знаходимо ту частину графіка, яка лежить вище вісі абсцис . В даному випадку ця умова виконується для любих значеннях х. Записуємо відповідь: (- ∞;+ ∞)

План розв’язання: Знайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а вершина лежить на вісі абсцис. ax2+bx+c≥0, a>0 За знаком нерівності знаходимо ту частину графіка, яка лежить вище вісі абсцис та враховуємо точку перетину з віссю Ох. В даному випадку ця умова виконується при любих значеннях х. Записуємо відповідь: (- ∞;+ ∞)

Розглянемо та запишемо алгоритм розв’язування нерівності ax2+bx+c0 графічним способом

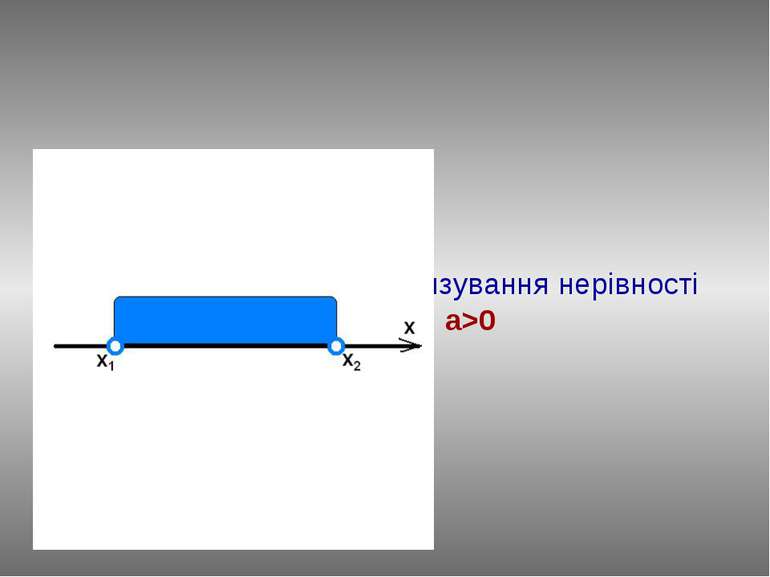
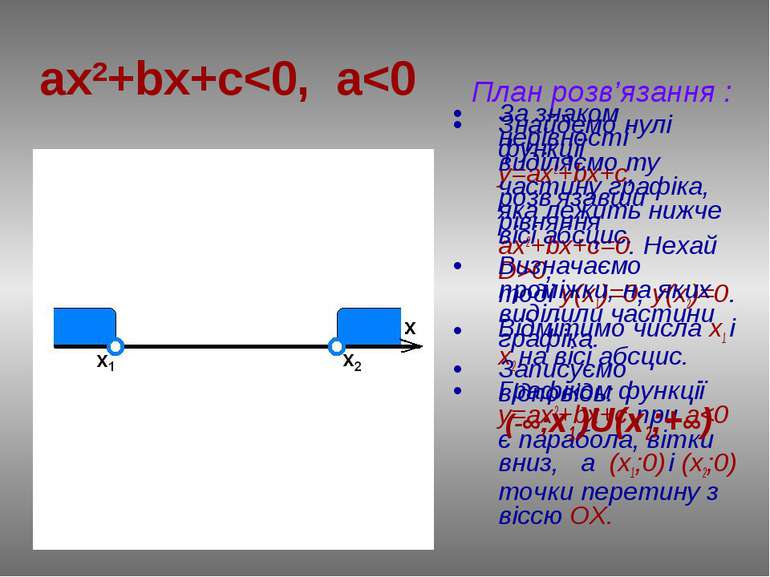
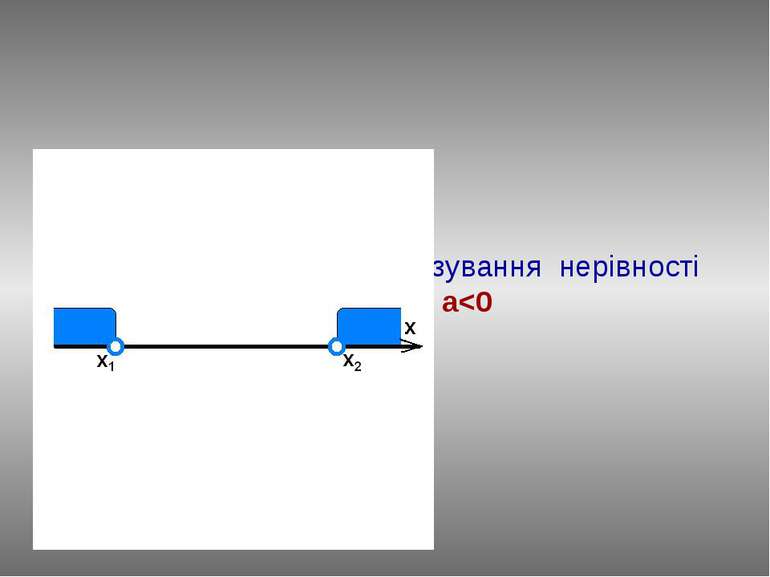
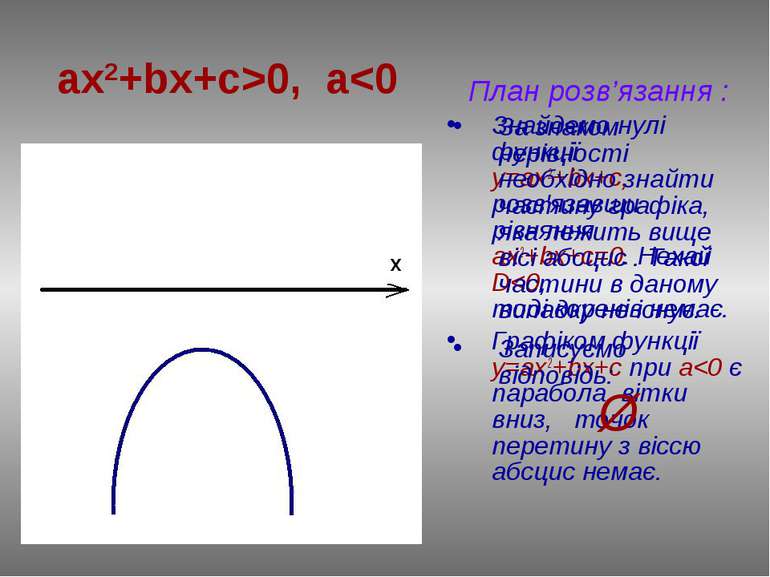
ax2+bx+c0 План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D>0, тоді у(х1)=0, у(х2)=0. Відмітимо числа х1 і х2 на вісі абсцис. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а (х1;0) і (х2;0) точки перетину з віссю ОХ. За знаком нерівності виділяємо ту частину графіка, який лежить нижче вісі абсцис . Визначаємо проміжок на якому виділили частину графіка. Записуємо відповідь: (х1 ; х2)

Повторимо алгоритм розв’язування нерівності ax2+bx+c0

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

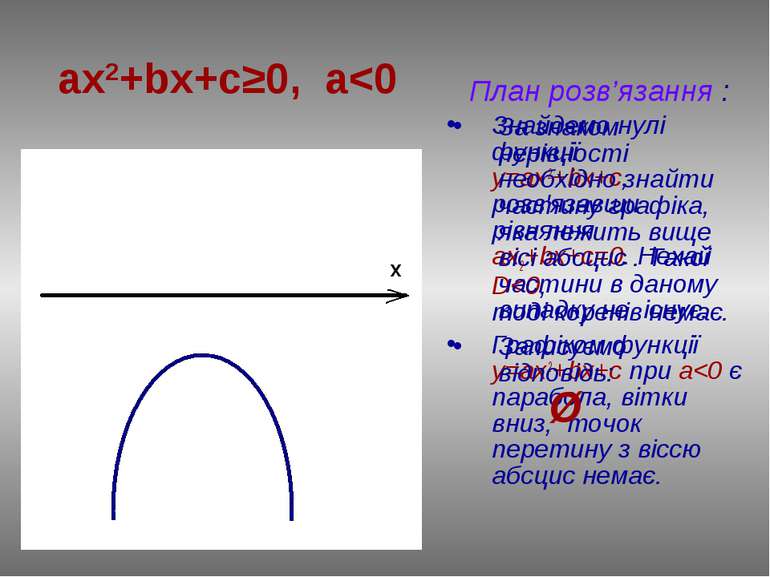
План розв’язання : Зайдемо нулі функції у=ax2+bx+c, розв’язавши рівняння ах2+bx+c=0. Нехай D0 є парабола, вітки вгору і точок перетину з віссю абсцис немає. ax2+bx+c0 За знаком нерівності знаходимо ту частину графіка, яка лежить нижче вісі абсцис . Такої частини в даному випадку не існує. Записуємо відповідь: Ø

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, вершина лежить на вісі абсцис. ax2+bx+c0 За знаком нерівності знаходимо ту частину графіка, яка лежить нижче вісі абсцис. Такої частини в даному випадку не існує. Записуємо відповідь: Ø

Розглянемо та запишемо алгоритм розв'язування нерівності ax2+bx+c>0, a>0 графічним способом

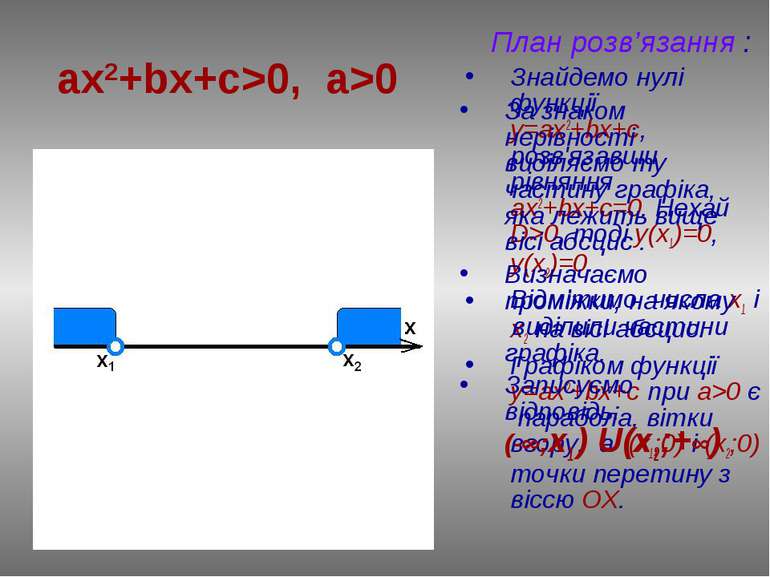
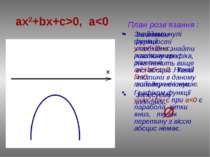
План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D>0, тоді у(х1)=0, у(х2)=0. Відмітимо числа х1 і х2 на вісі абсцис. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а (х1;0) і (х2;0) точки перетину з віссю ОХ. ax2+bx+c>0, a>0 За знаком нерівності виділяємо ту частину графіка, яка лежить вище вісі абсцис . Визначаємо проміжки, на якому виділили частини графіка. Записуємо відповідь: (-∞;х1 ) U(х2;+∞)

Повторимо алгоритм розв'язування нерівності ax2+bx+c>0, a>0

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D0 є парабола, вітки вгору , точок перетину з віссю абсцис немає. ax2+bx+c>0, a>0 За знаком нерівності необхідно знайти частину графіка, яка лежить вище вісі абсцис . В даному випадку ця умова виконується для любих значень х. Записуємо відповідь: (- ∞;+ ∞)

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a>0 є парабола, вітки вгору, а вершина лежить на вісі абсцис. ax2+bx+c>0, a>0 За знаком нерівності необхідно знайти частину графіка, яка лежить вище вісі абсцис і враховуємо точку пере тину з віссю Ох. В даному випадку ця умова виконується при всіх значеннях х крім х0. Записуємо відповідь: (- ∞;х0) U(x0;+ ∞)

Розглянемо та запишемо алгоритм розв'язування нерівності ax2+bx+c≤0, a

ax2+bx+c≤0, a

Повторимо алгоритм розв'язування нерівності ax2+bx+c≤0, a

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

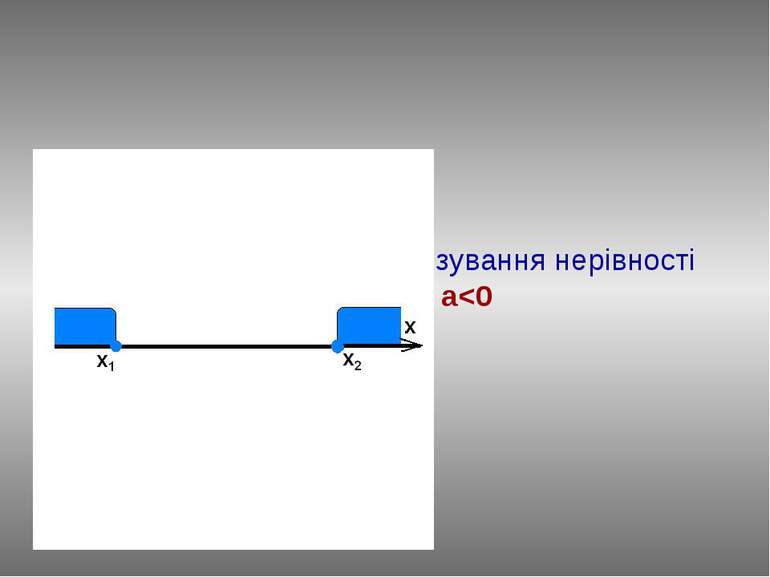
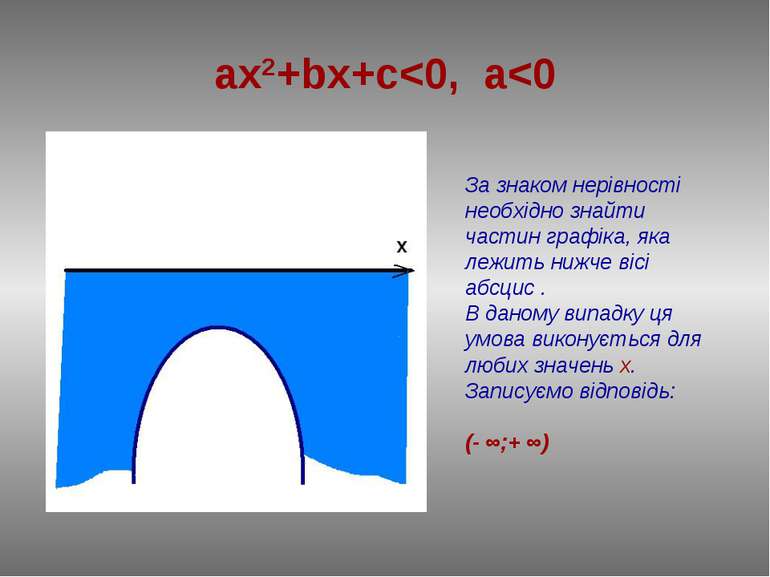
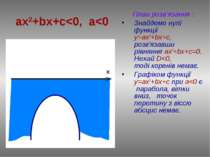
План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння х2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a

Розглянемо та запишемо алгоритм розв'язування нерівності ax2+bx+c≥0, a

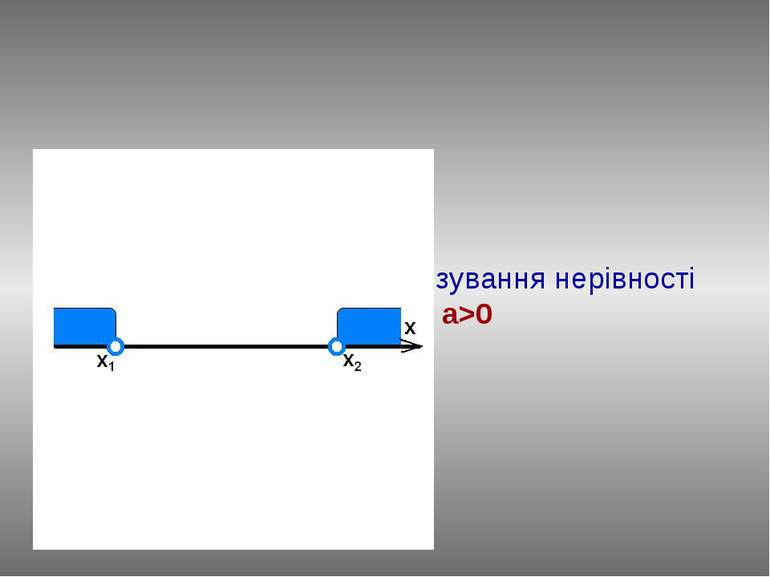
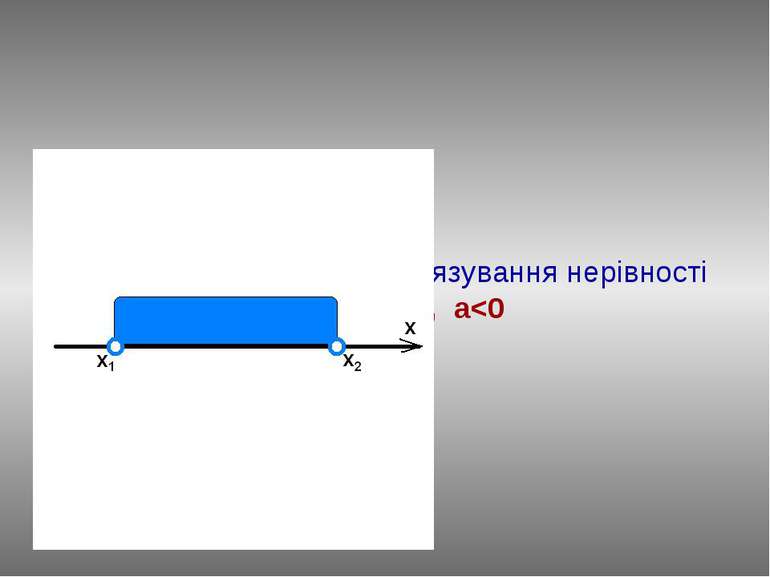
План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D>0, тоді у(х1)=0, у(х2)=0. Відмітимо числа х1 і х2 на вісі абсцис. Графіком функції у=ax2+bx+c при a

Повторимо алгоритм розв'язування нерівності ax2+bx+c≥0, a

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a

Розглянемо та запишемо алгоритм розв'язування нерівності ax2+bx+c

ax2+bx+c

Повторимо алгоритм розв'язування нерівності ax2+bx+c

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D

ax2+bx+c

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a

Розглянемо та запишемо алгоритм розв'язування нерівності ax2+bx+c>0, a

ax2+bx+c>0, a

Повторимо алгоритм розв'язування нерівності ax2+bx+c>0, a

При знаходженні коренів рівняння ах2 + bx + c=0 можливі інші випадки: D

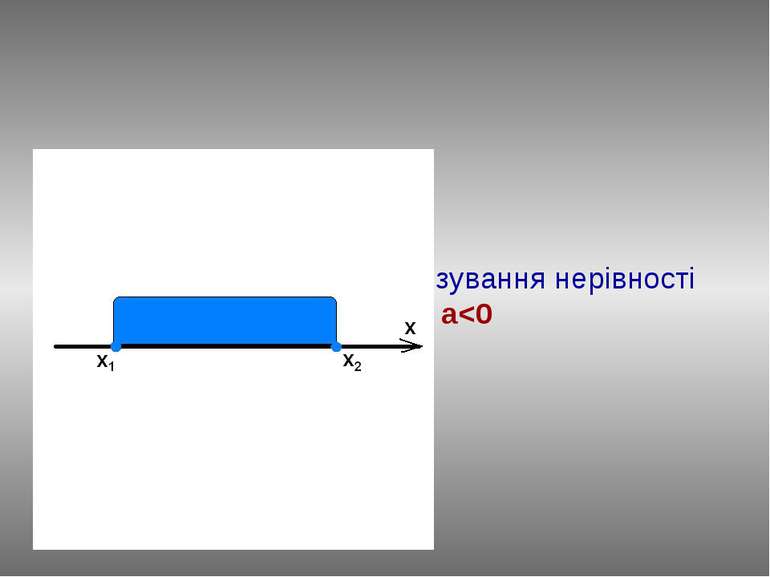
План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D

План розв’язання : Знайдемо нулі функції у=ax2+bx+c, розв'язавши рівняння ах2+bx+c=0. Нехай D=0, тоді рівняння має корінь х0= -b/2a. Графіком функції у=ax2+bx+c при a0, a

Даценко Світлана Олександрівна Вчитель математики Ставищенський НВК № 2 ім. О.С. Паланського смт Ставище Київської області 2012 рік