Презентація на тему:
Розв’язування лінійних нерівностей і систем нерівностей з однією змінною

Тема 2 Розв’язування лінійних нерівностей і систем нерівностей з однією змінною Лінійна нерівність з однією змінною. Рівносильні нерівності Система (та сукупність) нерівностей з однією змінною Числові проміжки. Переріз і об'єднання проміжків Нерівності, що містять модуль Розв’язування вправ. Самостійна робота Розв’язування систем ( та сукупностей) лінійних нерівностей з однією змінною. Доведення нерівностей Розв’язування вправ. Самостійна робота Розв'язування вправ

Готуємося до уроку Використано матеріали Бібліотеки електронних наочностей “Алгебра 7-9 клас”. Робота вчителя СЗОШ І- ІІІ ступенів № 8 м. Хмельницького Кравчук Г.Т. Мультимедійні технології на уроках алгебри 2011 рік

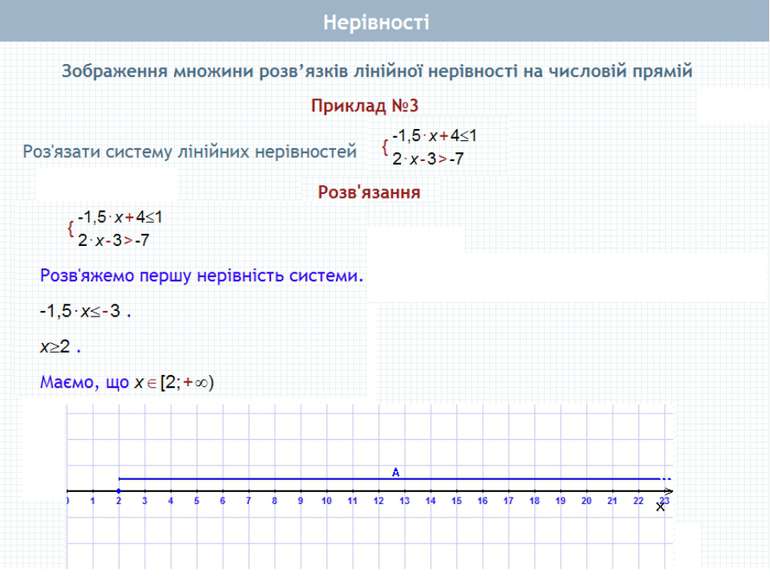
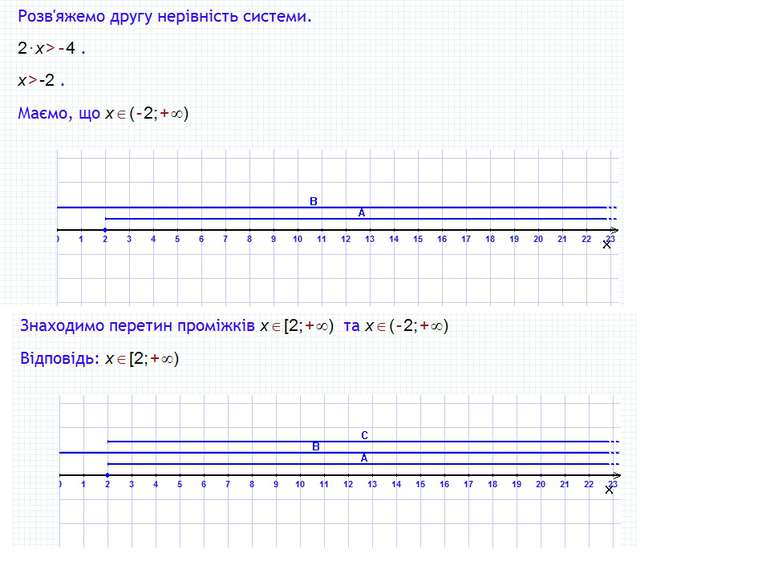
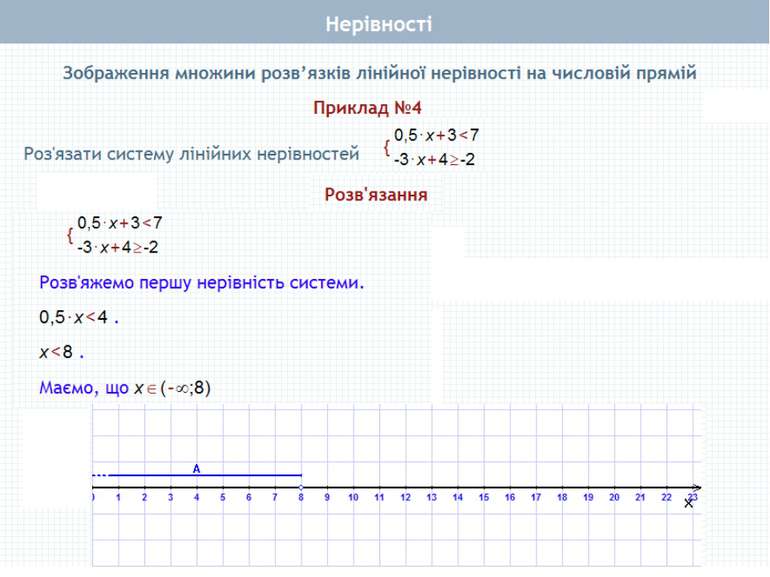
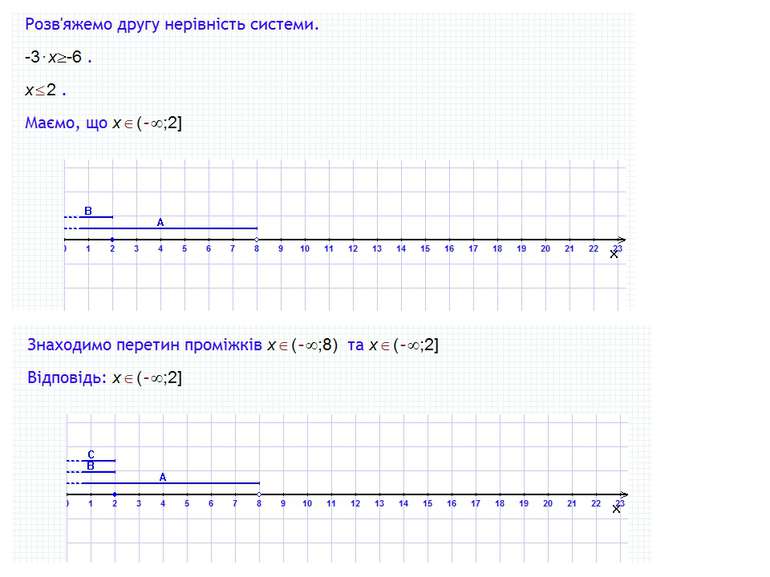
Пункт 2.2. Розв'язок системи нерівностей. Розв'язування систем нерівностей Приклади, що приводять до системи нерівностей Розв'язування подвійної нерівності Приклади Система лінійних нерівностей з однією змінною

Пригадайте В якому випадку кажуть, що два рівняння утворюють систему рівнянь? 2) Які розв'язки рівнянь системи є розв'язками самої системи рівнянь?

Пункт 2.2. Якщо доводиться знаходити спільні розв'язки двох або більшої кількості нерівностей з однією і тією самою змінною, то кажуть, що ці нерівності утворюють систему нерівностей. Систему нерівностей позначають фігурною дужкою: Як знайти розв'язок системи нерівностей

Пункт 2.2. Як знайти розв'язок системи нерівностей Розв'язок системи нерівностей – це значення змінної, яке задовольняє кожну нерівність системи. Розв'язати систему нерівностей – означає знайти всі її розв'язки або показати, що вона їх немає.

Пункт 2.2. Алгоритм: Щоб розв'язати систему нерівностей, спочатку розв'язують кожну нерівність окремо, а потім серед знайдених розв'язків знаходять розв'язки, спільні для обох нерівностей. Як знайти розв'язок системи нерівностей

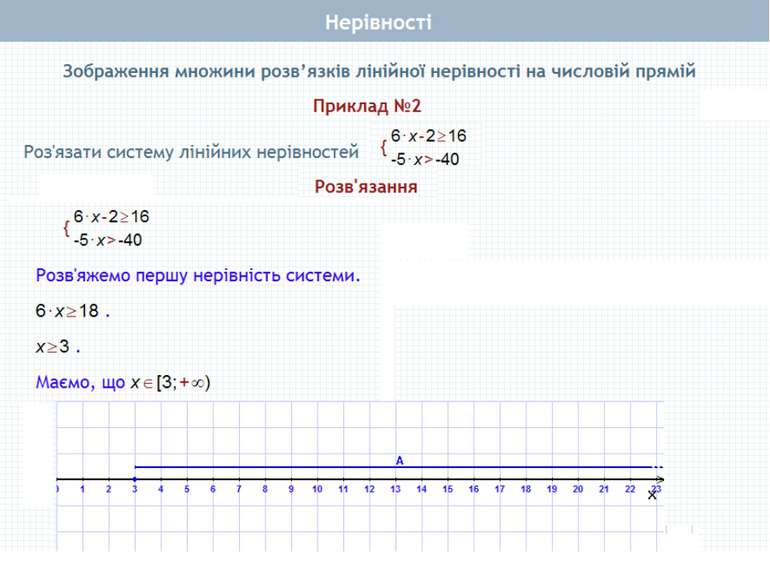
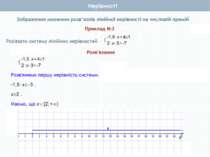
Пункт 2.2. Приклад: Розв'яжемо систему нерівностей Розв'язок кожної з нерівностей системи є числовим проміжком, відповідно (3; ∞) і (-2; ∞). Запис (3; ∞) (-2; ∞) означає переріз, тобто спільну частину даних проміжків. Розв'язком нерівності є проміжок (3; ∞). Як знайти розв'язок системи нерівностей Розв'язок системи нерівностей – це спільна частина числових проміжків, що є розв'язками кожної з нерівностей їх системи, яку називають їх перерізом і позначають за допомогою знака

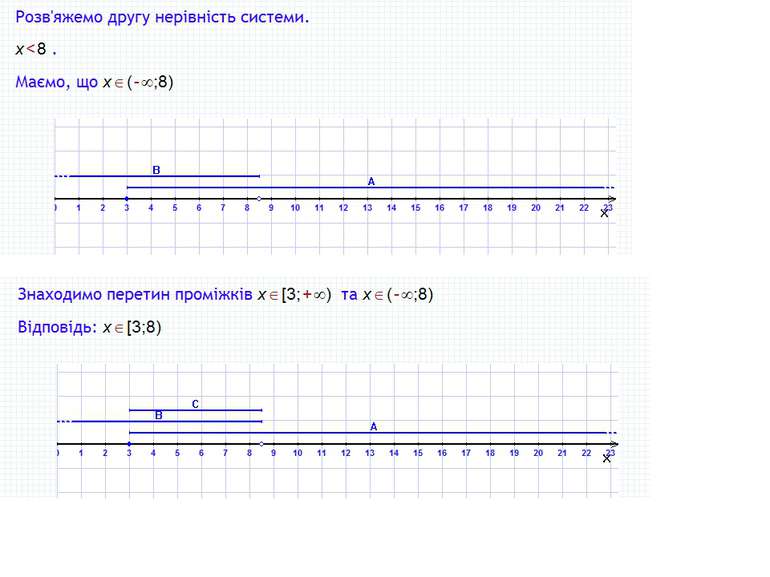
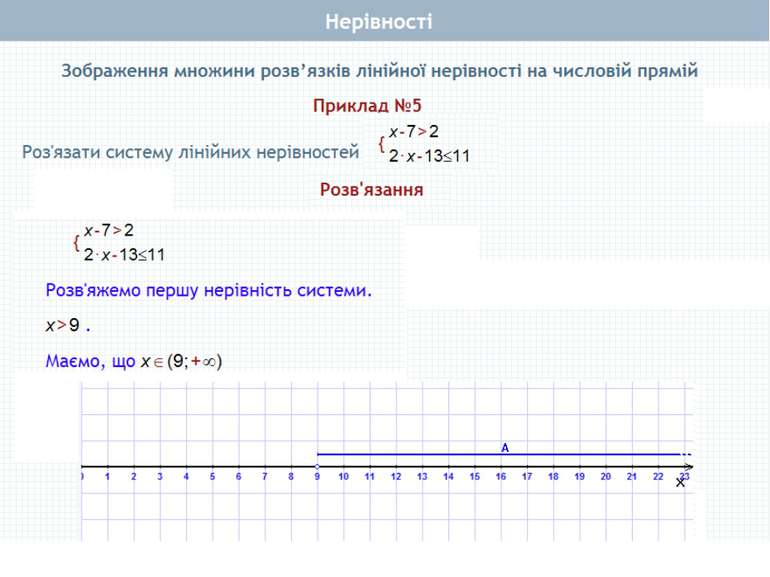
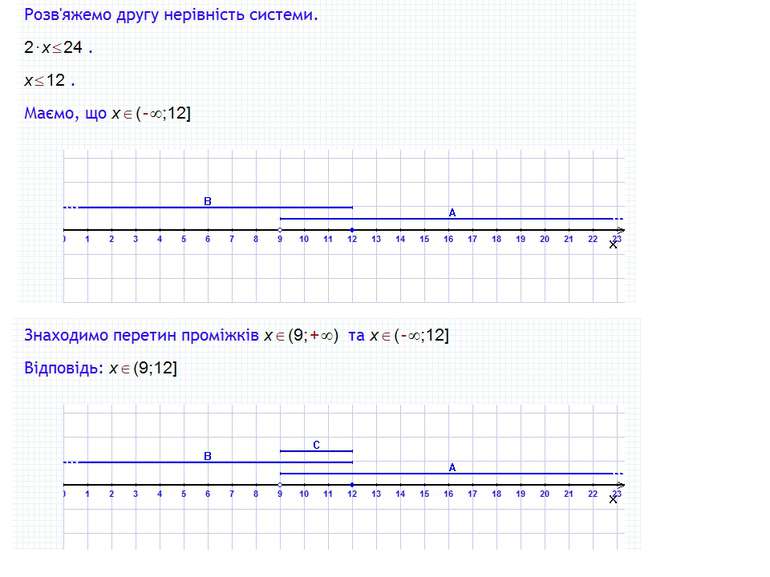
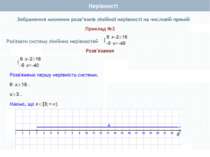
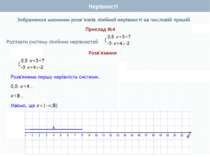
Пункт 2.2. Приклад 1 Розв'язати систему нерівностей Розв'язання: або З рисунка видно, що розв'язком системи є х≤1, тобто х (-∞; 1] Як знайти розв'язок системи нерівностей Розв'язок системи нерівностей – це спільна частина числових проміжків, що є розв'язками кожної з нерівностей їх системи, яку називають їх перерізом і позначають за допомогою знака

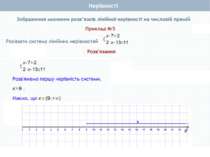
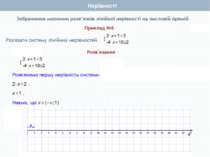
Приклад 3 Розв'язати систему нерівностей Розв'язання: Очевидно, що числові проміжки (-∞; 5) і (6; ∞) не мають жодного спільного числа. Тому система нерівностей не має розв'язку. У такому випадку кажуть, що переріз даних числових проміжків – порожня множина, яку позначають знаком . Нерівності

До систем лінійних нерівностей з однією змінною може привести розв'язування деяких нерівностей, які не є лінійними. До них належать, зокрема, нерівності виду: (ах + b)(сх + d) > 0, (ах + b)(сх + d) < 0, Для їх розв'язання використовують твердження: добуток або частка двох виразів додатні тоді і лише тоді, якщо обидва ці вирази мають однакові знаки; добуток або частка двох виразів від'ємні тоді і лише тоді, якщо ці вирази мають протилежні знаки. Отже, (ax + b)(cx + d)> 0 ( ) , якщо або Розв'язавши кожну з цих систем, отримаємо розв'язки даних нерівностей. Приклади, що приводять до систем нерівностей

Розв'язати нерівність: Розв'язання. Ця нерівність рівносильна сукупності таких двох систем: Розв'яжемо кожну з них. Розв'язком даної нерівності є числова множина, яка складається з чисел першого і другого отриманих числових проміжків. Така множина називається об'єднанням цих проміжків і позначається за допомогою знака U Отже, Числові проміжки в їх об'єднанні розташовують, як правило, в порядку зростання чисел Приклади, що приводять до систем нерівностей

Оскільки подвійна нерівність а

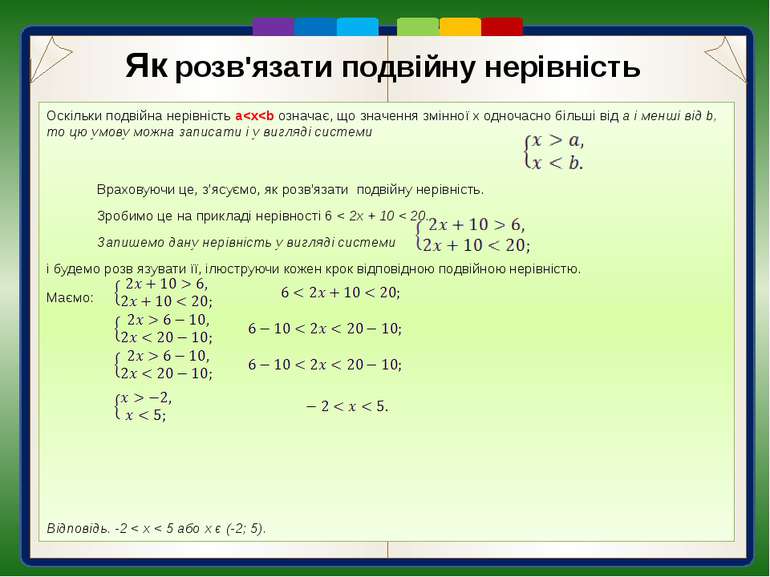
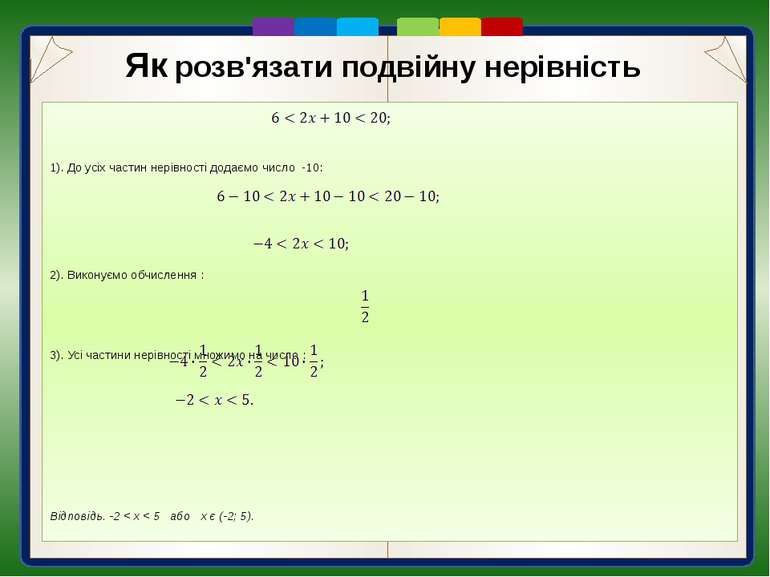
1). До усіх частин нерівності додаємо число -10: 2). Виконуємо обчислення : 3). Усі частини нерівності множимо на число : Відповідь. -2 < х < 5 або х є (-2; 5). Як розв'язати подвійну нерівність

Розв'яжемо нерівність: . Маємо: Відповідь. або х є (-4;-1). Як розв'язати подвійну нерівність

Коли дві лінійні нерівності з однією змінною утворюють систему? Як знаходять розв'язок системи лінійних нерівностей з однією змінною? Як називають спільну частину двох числових проміжків? Як можна дати означення розв'язку системи лінійних нерівностей з однією змінною, використавши поняття перерізу числових проміжків? Об'єднанням розв'язків яких двох систем лінійних нерівностей є числовий проміжок, що є розв'язком нерівності ? Як розв'язати подвійну нерівність? Проілюструйте на прикладі. Запитання для самоперевірки

Первинне закріплення вивченого матеріалу. Приклади

нерівності

нерівності

нерівності