Презентація на тему:
Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля

Жереб мені випав такий – серцем палким любити! Ласку весни, розкіш, красу, сонця ясне проміння! Ома р Хайя м

Світ – це море. Плисти бажаєш – Збудуй судно З добрих справ.

Тема заняття Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля

Знання – це скарб, йому ціни не зложиш. Визбируй же його, де тільки зможеш. Омар Хайям “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Виберіть довільних 4 кольори 1 8 2 3 4 7 6 5 “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Розв’язати вправи: а) |x| = 3 Відповідь: x = 3, x = - 3. б) |y| = 0,2 Відповідь: y = 0,2, y = - 0,2. в) |t| = -7 Відповідь: . г) |z| = 0 Відповідь: z = 0. “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Розв’язати вправи: д) |x| < 4. Відповідь: x (-4; 4); е) |x| > 5. Відповідь: x (-∞; -5) (5; ∞).     “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Знайти відповідь: 1) |x - 3| = 2 а) x1 = - 1, x2 = - 5 2) |3 - x| = 2 3) |x + 3| = 2 б) x1 = 1, x2 = 5 в) x1 = - 1, x2 = 5 “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

План розв’язування рівнянь, нерівностей, графіків, які містять знак модуля область визначення; нулі підмодулевих виразів; позначення даних чисел на числовій осі з урахуванням області визначення; розкриття модуля на кожному з утворених проміжків; перевірка належності коренів (розв’язків) даному проміжку. “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Спростити вираз |x – 2| + |3 – x| = |x – 2| + |3 – x| = |x – 2| + |3 – x| = |x - 2| + |3 - х| D(y) = R; x - 2 = 0; x = 2; 3 - x = 0; x = 3. а) (-∞; 2]: б) (2; 3): в) [3; ∞): “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля” - + -x + 2 + 3 – x = 5 – 2x; x - 2 + 3 – x = 1; x – 2 – 3 + x = 2x – 5.

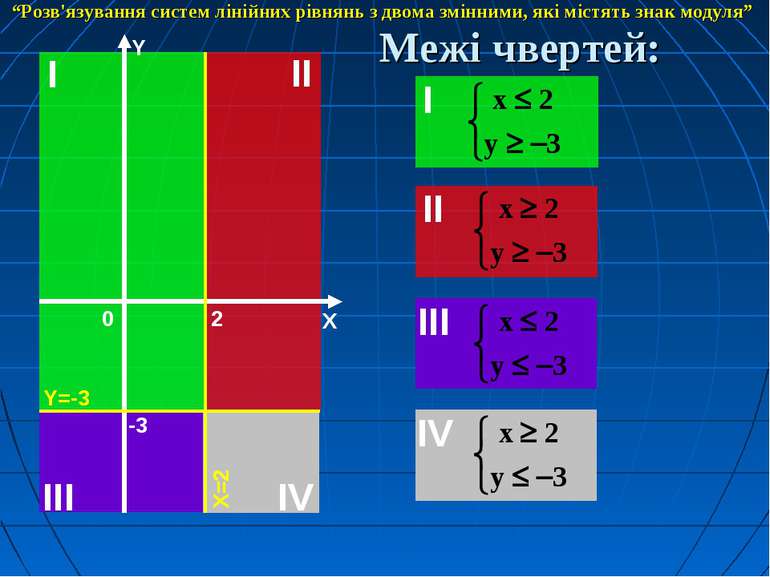
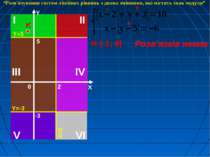
Межі чвертей: “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

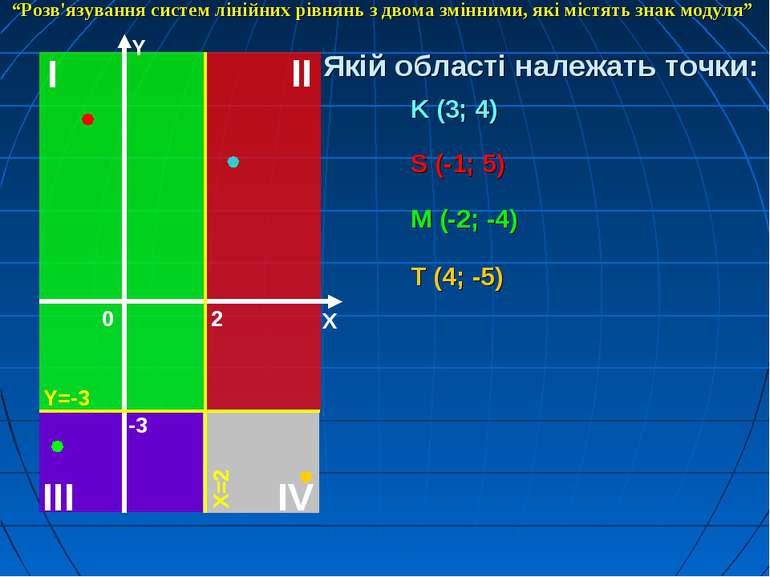
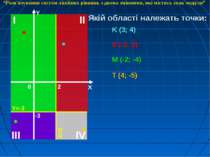
Якій області належать точки: K (3; 4) S (-1; 5) M (-2; -4) T (4; -5) “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

D(y): x R y R x = 2; y = -3; y = 5. Нулі підмодулевих виразів: “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

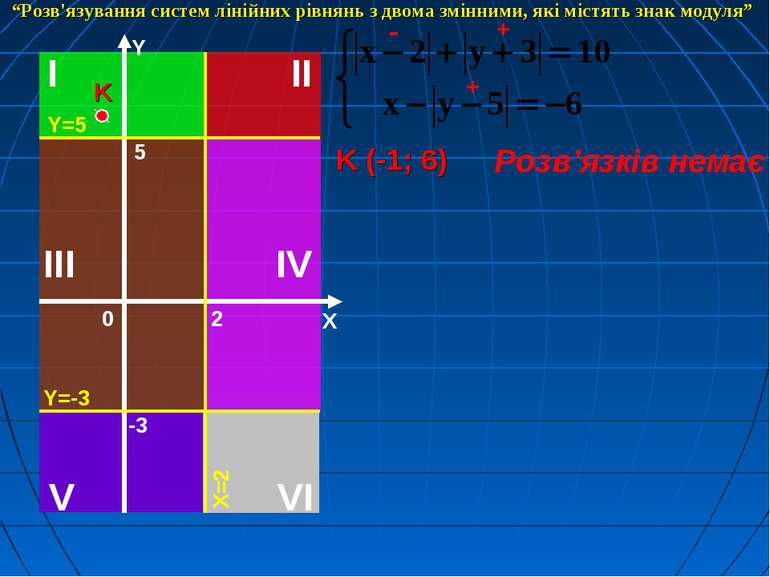
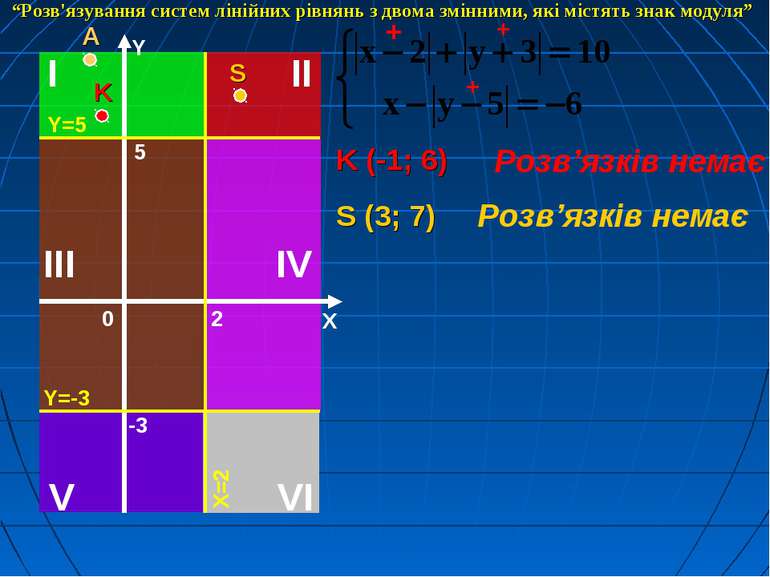
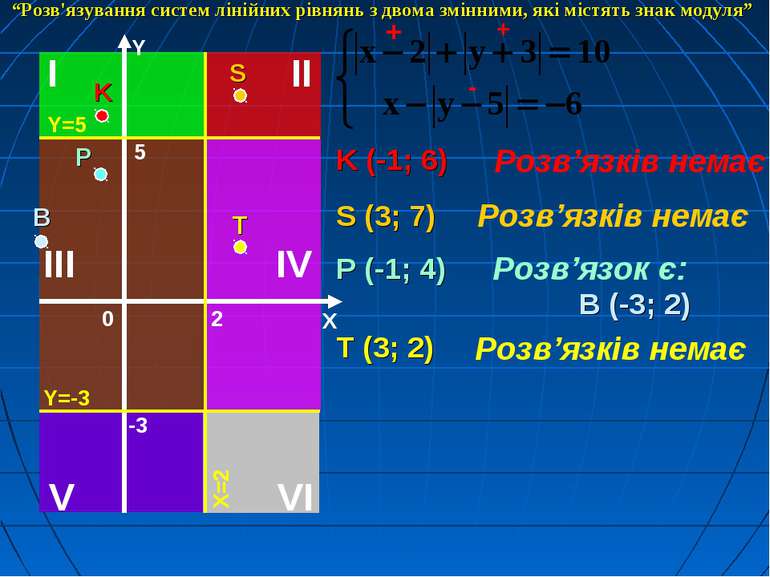
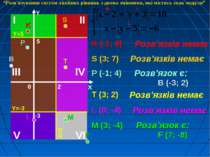
K (-1; 6) Розв’язків немає + - + “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

K (-1; 6) Розв’язків немає + + + S (3; 7) Розв’язків немає “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

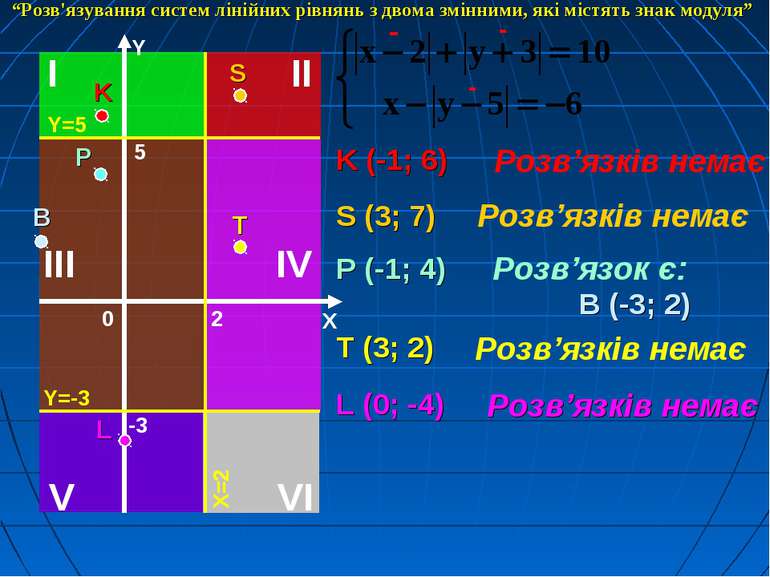
K (-1; 6) Розв’язків немає + - - S (3; 7) Розв’язків немає P (-1; 4) Розв’язок є: В (-3; 2) “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

K (-1; 6) Розв’язків немає + + - S (3; 7) Розв’язків немає P (-1; 4) Розв’язок є: В (-3; 2) T (3; 2) Розв’язків немає “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

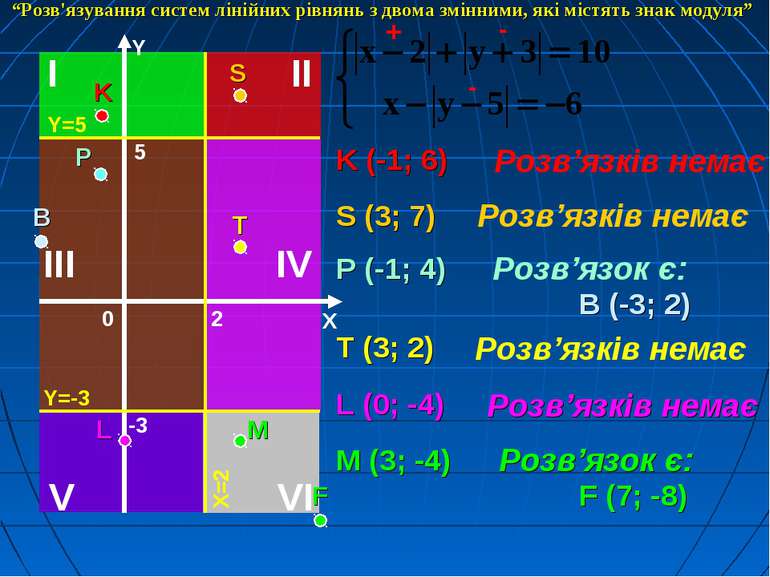
K (-1; 6) Розв’язків немає - - - S (3; 7) Розв’язків немає P (-1; 4) Розв’язок є: В (-3; 2) T (3; 2) Розв’язків немає L (0; -4) Розв’язків немає “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

K (-1; 6) Розв’язків немає - + - S (3; 7) Розв’язків немає P (-1; 4) Розв’язок є: В (-3; 2) T (3; 2) Розв’язків немає L (0; -4) Розв’язків немає M (3; -4) Розв’язок є: F (7; -8) “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Я тільки знаю, що знання шукаю, В глибинні таємниці проникаю. Омар Хайям “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”

Домашнє завдання: “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля” Розв'язати систему: Скласти систему, підмодулевими нулями якої є: X = 2; X = -3; Y = 4.

Виберіть довільних 4 кольори 1 8 2 3 4 7 6 5 “Розв'язування систем лінійних рівнянь з двома змінними, які містять знак модуля”