Презентація на тему:
Розв’язування систем рівнянь другого степеня з двома змінними

Пункт 6.2. Розв’язування систем рівнянь з двома змінними Аналітичні способи. Приклади Графічний спосіб. Приклади Пригадайте 1). В якому випадку два лінійні рівняння з двома змінними утворюють систему рівнянь? 2). Що є розв'язком системи двох лінійних рівнянь з двома змінними?

Пункт 6.2. Розв’язування систем рівнянь з двома змінними Систему рівнянь другого степеня з двома змінними можуть утворювати два рівняння, кожне з яких є рівнянням другого степеня, або одне з них є рівнянням другого степеня а інше – рівнянням першого степеня. Розв'язок такої системи – це пара значень змінних, яка задовольняє обидва рівняння системи. Способи розв'язування систем: Підстановки Додавання Деякі штучні прийоми

Пункт 6.2. Аналітичні способи Приклад 1. Розв'язати систему рівнянь: І спосіб. Таку систему зручно розв'язувати способом підстановки. З першого рівняння виразимо змінну у через х і підставимо отриманий вираз у друге рівняння. Відповідь. (-2; 8) і (8; -2)

Тема 4 Квадратні нерівності та системи рівнянь другого степеня Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб. Розв’язування нерівностей другого степеня з однією змінною. Аналітичний спосіб Метод інтервалів Степінь рівняння з двома змінними. Розв’язування систем рівнянь з двома змінними Розв’язування вправ. Самостійна робота Розв’язування текстових задач складанням систем рівнянь з двома змінними

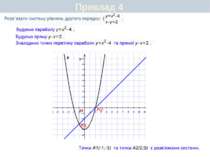
Пункт 6.2. Аналітичні способи Приклад 2. Розв'язати систему рівнянь: Розв'язуючи кожну з них отримаємо розв'язки першої системи: (4; 2) і (2; 4); розв'язки другої системи: (-4; -2) і (-2; -4). Відповідь. (-4; -2), (-2; -4), (4; 2), (2; 4).

Пункт 6.2. Аналітичні способи Приклад 1. Розв'язати систему рівнянь: Відповідь. (-2; 8) і (8; -2) ІІ спосіб. Рівняння системи є, по суті, сумою і добутком двох невідомих чисел. Тому, за теоремою, оберненою до теореми Вієта, можемо утворити квадратне рівняння, коренями якого є ці числа. z2-6z-16=0. Знаходимо його корені: z1=-2; z2=8. Отже, або і або і

Пункт 6.2. Аналітичні способи Приклад 2. Розв'язати систему рівнянь: Помножимо обидві частини другого рівняння на 2 і додамо почленно рівняння нової системи. Отже, дана система рівносильна сукупності таких двох систем:

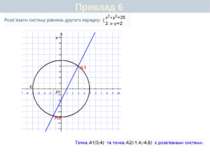
Пункт 6.2. Аналітичні способи Приклад 3. Розв'язати систему рівнянь: Розкладемо ліві частини обох рівнянь на множники. Оскільки (інакше праві частини обох рівнянь дорівнювали б нулю), то поділимо відповідні частини рівняння одна на одну. Підставимо це значення х у друге рівняння останньої системи Відповідь. (3; 1), (-3; -1).

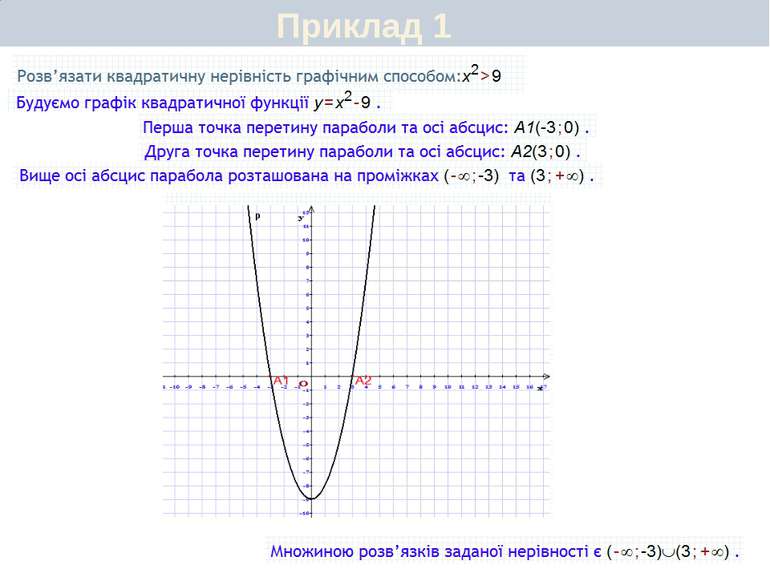
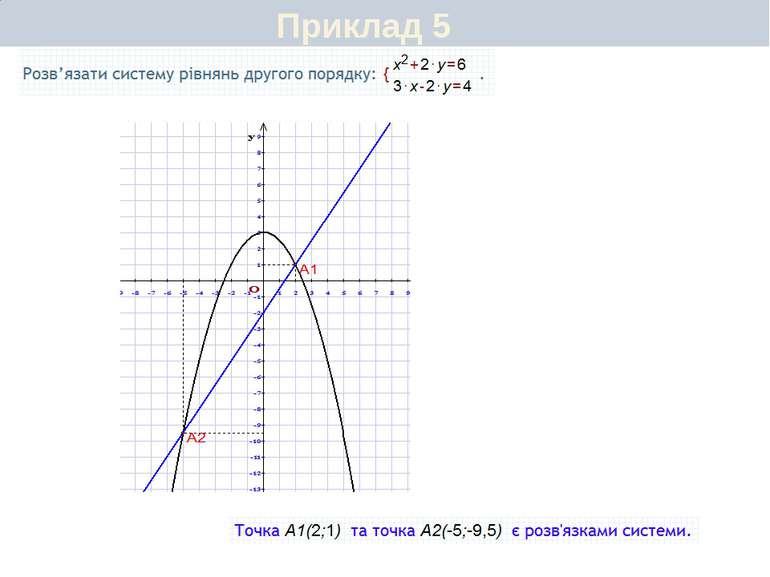
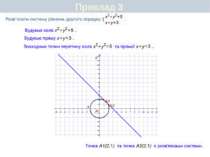
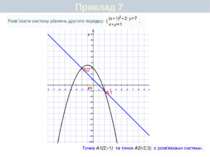
Графічний спосіб Приклад 1. Розв'язати систему рівнянь: Розв'яжемо дану систему рівнянь графічним способом. Побудуємо графіки рівнянь системи, тобто графіки функцій у = х2 + 3 і у = - х+5. Координати точок прямої є розв'язками рівняння х+у=5, а координати точок параболи у = х2 + 3 – розв'язками рівняння у - х2 = 3. Точки А (-2; 7) і В (1; 4) належать як прямій, так і параболі, тобто є спільними для них. Тому координати точок А і В є розв'язками даної системи. Відповідь. (-2; 7) і (1; 4)

Приклад 1

Приклад 2

Приклад 3

Приклад 4

Приклад 5

Приклад 6

Приклад 7

Запитання для самоперевірки Які рівняння можуть утворювати систему двох рівнянь другого степеня з двома змінними? Як встановити,чи є дана пара чисел розв'язком системи двох рівнянь другого степеня з двома змінними? Які ви можете назвати способи розв'язування систем двох рівнянь другого степеня з двома змінними? Поясніть їх суть на прикладах.