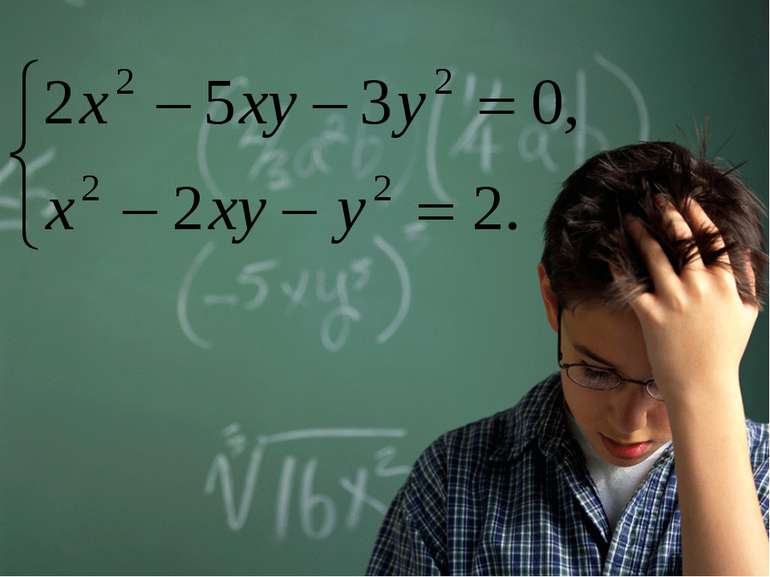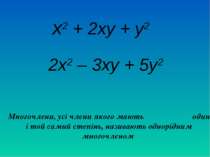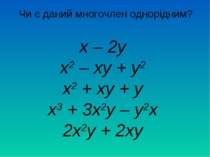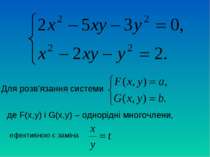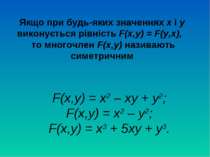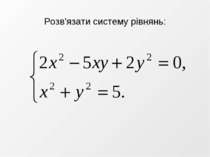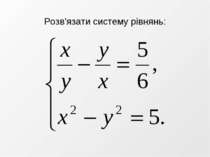Презентація на тему:
Розв’язування систем рівнянь методом заміни змінної

03 лютого 2010 року 3 лютого 1957 року 3 лютого 1966 року 3 лютого 1847 року

3 лютого Класна робота

якщо потрібно знайти утворюють систему Два і більше рівнянь всі їхні спільні розв'язки Два і більше рівнянь утворюють систему, якщо потрібно знайти всі їх спільні розв’язки

пара значень змінних, Розв'язком системи рівнянь з двома змінними називається в правильну рівність яка перетворює кожне рівняння системи Розв’язком системи рівнянь з двома змінними називається пара значень змінних, яка перетворює кожне рівняння системи в правильну рівність

знайти всі її розв'язки Розв'язати систему рівнянь або довести, що їх немає означає Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що їх немає

Два рівняння називаються рівносильними, якщо всі розв'язки першого рівняння … є розв'язками другого і, навпаки, всі розв'язки другого рівняння є розв'язками першого

Ви познайомилися з такими методами розв’язування систем рівнянь, як … графічний, метод додавання, метод підстановки

Які недоліки графічного методу розв’язування систем рівнянь? Коли графічний метод розв’язування рівнянь є ефективним? У чому полягає сутність методу підстановки? Які системи рівнянь можна розв’язати методом додавання?

3 лютого Класна робота Розв’язування систем рівнянь методом заміни змінної Ключові поняття уроку: однорідні многочлени; симетричні многочлени; метод заміни змінної

формування поняття однорідного многочлена формування поняття симетричного многочлена формування умінь і навичок розв’язування систем рівнянь методом заміни змінної вироблення вмінь і навичок застосовувати цей спосіб під час розв’язування систем рівнянь

х2 + 2ху + у2 2х2 – 3ху + 5у2 Многочлени, усі члени якого мають один і той самий степінь, називають однорідним многочленом

х – 2у х2 – ху + у2 х2 + ху + у х3 + 3х2у – у2х 2х2у + 2ху Чи є даний многочлен однорідним?

Для розв’язання системи де F(x,y) і G(x,y) – однорідні многочлени, ефективною є заміна

Якщо при будь-яких значеннях х і у виконується рівність F(x,y) = F(y,х), то многочлен F(x,y) називають симетричним F(x,y) = х2 – ху + у2; F(x,y) = х2 – у2; F(x,y) = х3 + 5ху + у3.

З’ясуйте, чи є даний многочлен симетричним: х4 + х2у + у4; (х + у)(х2 + у2); (х2 + у)(х + у2); х2 + ху + у.

Будь-який симетричний многочлен від х і у можна подати у вигляді многочлена від u та v такі, що u=x+y; v=xy. Теорема:

Розв'язати систему рівнянь:

Розв'язати систему рівнянь:

формування поняття однорідного многочлена формування поняття симетричного многочлена формування умінь і навичок розв’язування систем рівнянь методом заміни змінної вироблення вмінь і навичок застосовувати цей спосіб під час розв’язування систем рівнянь

Домашнє завдання Опрацювати п. 18 підручника До прикладу 6 на с. 173 скласти план розв’язування системи Розв’язати систему рівнянь методом заміни змінної № 18.2(2) Додаткове завдання Розв’язати систему рівнянь способом заміни змінної:

Дякую за співпрацю