Презентація на тему:
Розв’язування нерівностей другого степеня з однією змінною. Аналітичні способи

Тема 4 Квадратичні нерівності та системи рівнянь другого степеня Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб. Розв’язування нерівностей другого степеня з однією змінною. Аналітичний спосіб Метод інтервалів Степінь рівняння з двома змінними. Розв’язування систем рівнянь з двома змінними Розв’язування вправ. Самостійна робота Розв’язування текстових задач складанням систем рівнянь з двома змінними

Пункт 5.2. Пригадайте Як розкласти квадратний тричлен на лінійні множники? В якому випадку це можна зробити? За якої умови добуток двох множників: а) додатне число; б) від'ємне число? Розв’язування нерівностей другого степеня з однією змінною. Аналітичні способи.

Запитання для самоперевірки Які два випадки слід розрізняти, розв'язуючи квадратну нерівність аналітичним способом? Як розв'язують квадратну нерівність, якщо їх ліву частину можна розкласти на множники? Як розв'язують квадратну нерівність, якщо їх ліву частину не можна розкласти на множники?

Пункт 5.2. Якщо квадратний тричлен ах2 + bх + с має два корені х1 і x2 то його можна розкласти на множники: ах2 + bх + с=а(х—х 1)(х—х2). У такому випадку розв'язування квадратної нерівності зводиться до розв'язання двох систем лінійних нерівностей. Спосіб розкладання лівої частини нерівності на множники

Пункт 5.2. Розв'язання Розв'язків немає Відповідь. Спосіб розкладання лівої частини нерівності на множники Приклад 1. Розв'язати нерівність: 2х2 - х - 1 < 0.

Пункт 5.2. Розв'язання Відповідь. Спосіб розкладання лівої частини нерівності на множники Приклад 2. Розв'язати нерівність:

Пункт 5.2. Розв'язання Відповідь. Розв'язків немає Спосіб розкладання лівої частини нерівності на множники Приклад 3. Розв'язати нерівність: Дана нерівність немає розв’язку, бо при будь-якому дійсному значенні х.

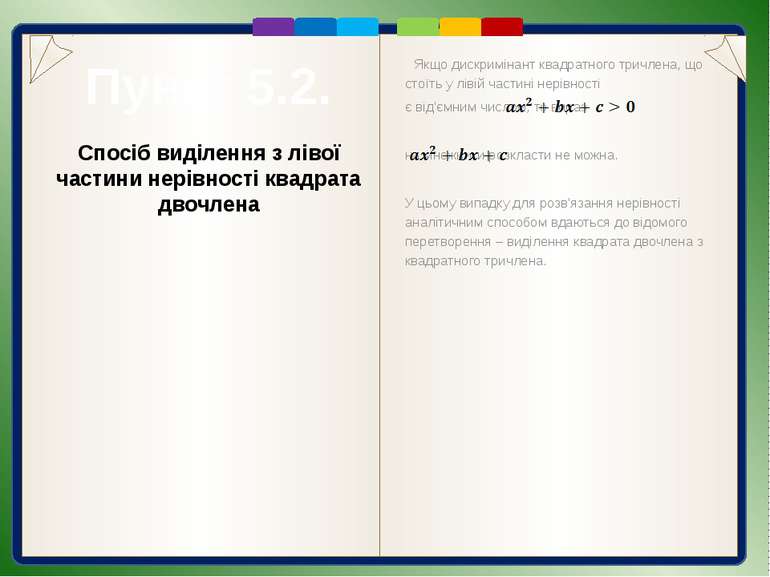
Пункт 5.2. Якщо дискримінант квадратного тричлена, що стоїть у лівій частині нерівності є від'ємним числом, то вираз на множники розкласти не можна. У цьому випадку для розв'язання нерівності аналітичним способом вдаються до відомого перетворення – виділення квадрата двочлена з квадратного тричлена. Спосіб виділення з лівої частини нерівності квадрата двочлена

Пункт 5.2. Розв'язання Виділимо з тричлена квадрат двочлена. Маємо: Очевидно, що вираз при будь-якому дійсному значенні х набуває додатного значення, тобто при всіх дійсних значеннях х. Тому нерівність не має розв'язків. Спосіб виділення з лівої частини нерівності квадрата двочлена Приклад 4. Розв'язати нерівність:

Пункт 5.2. Розв'язання Спосіб виділення з лівої частини нерівності квадрата двочлена Приклад 5. Розв'язати нерівність: Відповідь. Х (- ∞; ∞)

Первинне закріплення вивченого матеріалу Встановіть відповідність між даними нерівностями та їх розв'язками 1. 2. 4. 3. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. А В Д Г Е Б Є Ж З И І Ї Й К Л