Презентація на тему:
Похідна

Математика - це мистецтво називати різні речі одним і тим же ім'ям.                                                   А. Пуанкаре Не достатньо знати, необхідно також застосовувати.  Анатоль Франс  Ніколи не соромся запитувати про те, чого не знаєш.

Тема 1. Матриці та визначники Лекція 1. Матриці та дії на ними

план Поняття матриці. Види матриць Дії над матрицями Визначники та їх властивості Обернена матриця. Властивості. Обчислення. Ю. М. Перегуда

Історична довідка

Теорія матриць використовується: В фізиці та інших прикладних науках матриці – є способом запису даних та їх перетворення. В програмуванні – в написанні програм (їх ще називають массивами). Широко використовуються в техніці ( наприклад будь-яке зображення на екрані – це двомірна матриця, елементами якої є кольори точок). Обернені матриці використовують при програмуванні трьохмірної графіки.  В військовій справі (наприклад, Є дві системи зброї, одна з яких ефективна проти одного виду цілі (високо літаючих), інша проти другого( низько літаючих) В результаті розрахунків ефективності можна скласти платіжну матрицю, елементами якої будуть ймовірності враження цілі комплексами. Розв'язавши дану задачу можна знайти оптимальне співвідношення даних систем зброї) “теорія матриць – це арифметика вищої математики” Р. Беллман

Означення

ВИДИ МАТРИЦЬ Прямокутна . Матриця-рядок. Матриця-стовпець.

Квадратна Діагональна Одинична

Нульова Трикутна Транспонована

Дії над матрицями Додавання та віднімання матриць Множення матриці на число Множення двох матриць

Означення

Властивості операції додавання: Комутативність: . Асоціативність: . Додавання нульової матриці до матриці не змінює : .

Означення

Властивості множення матриці на число ; ; ; ;

Означення

властивості множення матриць: - не комутативність. - асоціативність. ; - дистрибутивність відносно додавання. .

Означення

Означення

Означення

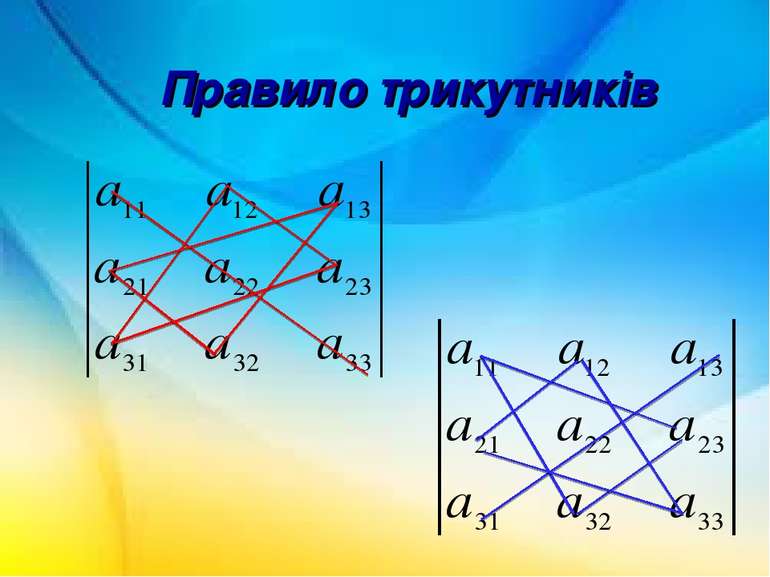
Обчислення визначника третього порядку Правило трикутників Правило Саррюса Метод розкладу визначника за елементами рядка (стовпця)

Правило трикутників

Правило Саррюса

Розклад визначника третього порядку

Основні властивості визначників: Якщо всі елементи деякого рядка (стовпця) визначника дорівнюють нулю, то такий визначник дорівнює нулю. Якщо у визначнику поміняти місцями два рядки (стовпці), то знак визначника зміниться на протилежний. Якщо у визначнику елементи деякого рядка (стовпця) рівні відповідним елементам іншого рядка (стовпця), то такий визначник дорівнює нулю.

Основні властивості визначників: Якщо всі елементи деякого рядка (стовпця) помножити на число , то значення визначника також помножиться на . Визначник, у якого всі елементи деякого рядка (стовпця) пропорційні відповідним елементам іншого рядка (стовпця), дорівнює нулю. Якщо до всіх елементів деякого рядка (стовпця) визначника додати або відняти відповідні елементи паралельного рядка (стовпця), помножені на довільне число, то значення цього визначника не зміниться.

Означення

Алгоритм знаходження оберненої матриці Обчислюють визначник . Обчислюють алгебраїчні доповнення всіх елементів матриці . Складають матрицю Складають обернену матрицю

Завдання на самопідготовку Вивчити основні означення , формули та теореми лекції 1. Література: Шумко Л.І. , Шумко Л.Г. Вища математика, курс лекцій, §1.1-1.3

Якщо ви хочете брати участь у великому житті, то наповнюйте свою голову математикою, поки є для цього можливість. Вона надасть вам потім величезну допомогу у всій вашій роботі.                   М.І. Калінін