Презентація на тему:
Похідна функції. Похідна складних функцій. Частинна похідна. Фізичний зміст похідної.
Завантажити презентацію
Похідна функції. Похідна складних функцій. Частинна похідна. Фізичний зміст похідної.
Завантажити презентаціюПрезентація по слайдам:
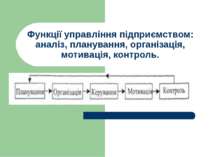
Похідна функції. Похідна складних функцій. Частинна похідна. Фізичний зміст похідної. Диференціал функції. Застосування диференціала для наближених обрахунків. Похідні і диференціали різних порядків функції від однієї змінної. Застосування повного диференціалу для наближених обрахунків.
Похідна функції. Похідною функції y=f(x) по аргументу х називається границя відношення приросту функції до приросту аргументу, коли останній прямує до нуля. Похідна функції y=f(x) позначається через : у , у (х), f , f (x), . Таким чином, за означенням, (1.3) Похідна від похідної називається похідною другого порядку, або другою похідною. Позначається таким чином : y , y2, f (x), f2(x), . Подібним чином вводиться поняття похідної n-ного порядку.
Таблиця формул диференціювання елементарних функцій.
Похідні складних функцій. Нехай у є функція від u : y=f(u), де u є функція від аргументу х : u= (x); тоді ми можемо записати y=f( (x)). Якщо для відповідних значень х і u існують похідні, то існує і похідна від у по х . причому має місце рівність : y =f(u)u =f[( (x)] (x). Приведемо таблицю основних формул диференціювання :
Таблиця основних формул диференціювання :
Дякую за увагу!
Схожі презентації
Категорії
