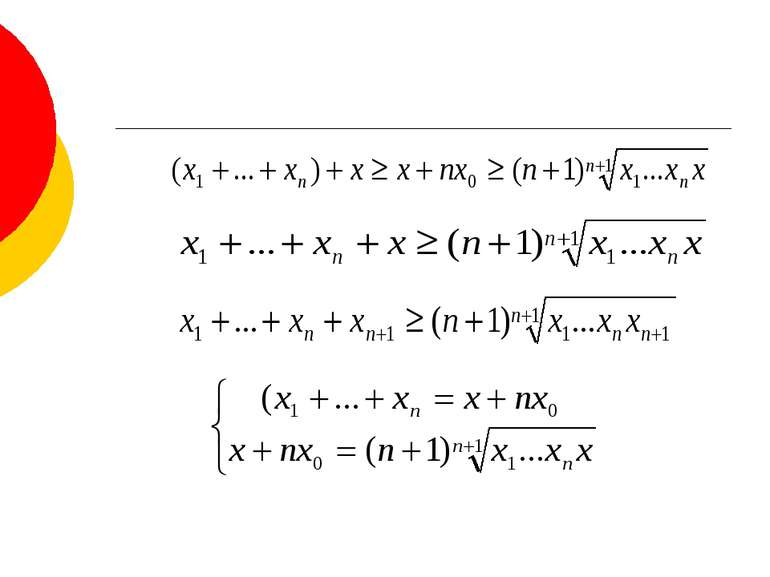Презентація на тему:
Застосування методу повної математичної індукції при розв’язуванні задач підвищеної складності

КІРОВОГРАДСЬКА МАЛА АКАДЕМІЯ НАУК УЧНІВСЬКОЇ МОЛОДІ НАУКОВЕ ТОВАРИСТВО УЧНІВ «ДИВОСВІТ» КІРОВГАДСЬКОГО ОБЛКОМПЛЕКСУ Застосування методу повної математичної індукції при розв’язуванні задач підвищеної складності

Мета: проаналізувати ефективність методу математичної індукції; дослідити застосування цього методу до розв'язування задач підвищеної складності.

Суть методу математичної індукції: доказуване твердження перевіряється для n=1 (початок або базис індукції); доводиться справедливість твердження для n=k+1 у припущенні справедливості твердження для n=k, тобто доводять, що А (k) А (k+1) (індукційний крок).

Доведіть, що ділиться на 81 при будь-якому значенні n. Перевіряємо, чи виконується задане твердження при n=1 -9*1-1=0, 0 ділиться на 81. Припускаємо, що задане твердження виконується і при n=k, тобто Доведемо, що задане твердження виконується при n=k+1, тобто .

за припущенням; 81k 81 – очевидно. Таким чином ділиться на 81 і задане твердження виконується при n=k+1. Отже, вираз ділиться на 81 при будь – якому натуральному n.

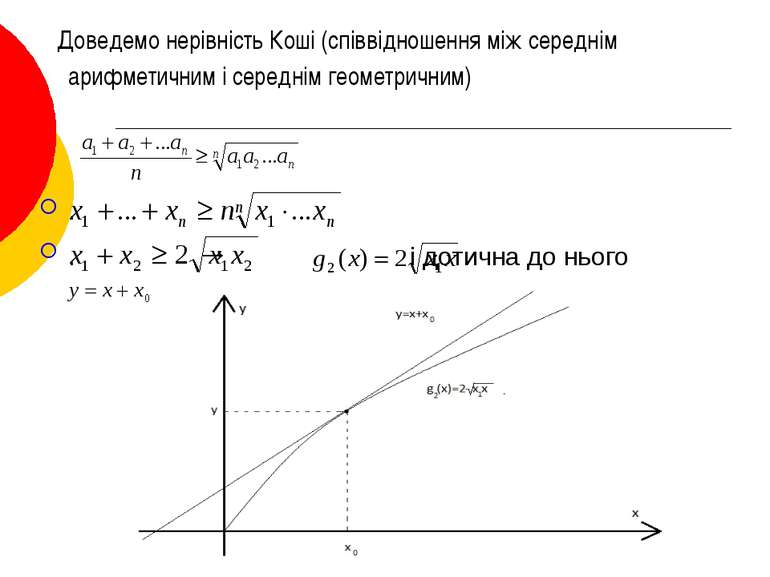
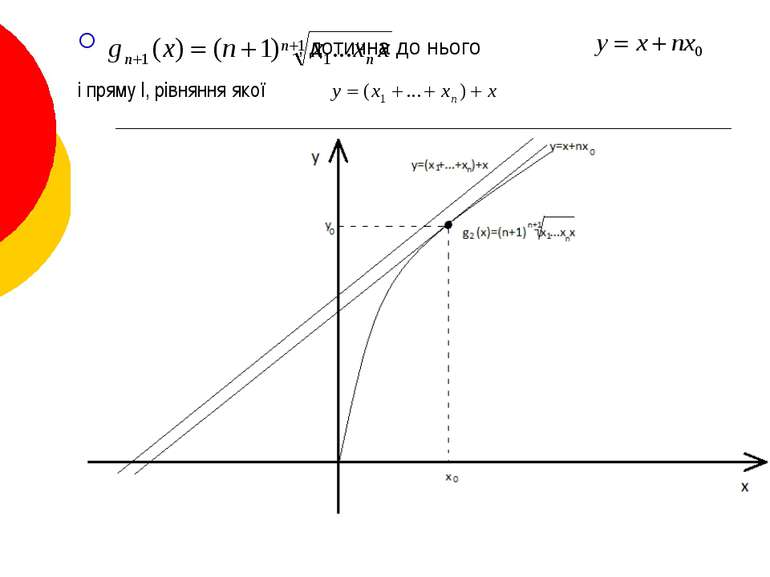
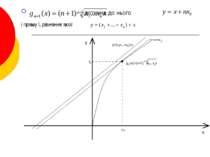
Доведемо нерівність Коші (співвідношення між середнім арифметичним і середнім геометричним) . . → і дотична до нього

. , дотична до нього і пряму l, рівняння якої

Дедуктивний метод Шерлока Холмса Суть дедуктивного методу 1. На основі всіх фактів і доказів будується повна картина злочину. 2. Відштовхуючись від отриманої картини злочину, шукається єдино відповідний їй звинувачуваний.

Результати досліджень: метод математичної індукції широко застосовується в різних відділах математики, починаючи від елементарного шкільного курсу й до найскладніших областей математичного дослідження; метод математичної індукції – один із найефективніших методів розв’язування задач підвищеної складності.

“Розуміння і вміння застосовувати принцип математичної індукції є добрим критерієм зрілості, яка цілковито необхідна математику” А.М. Колмогоров

Дякую за увагу!