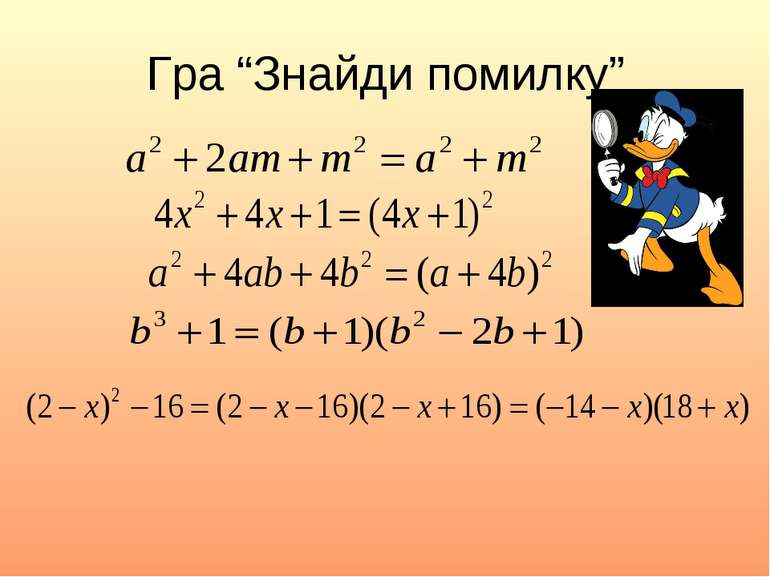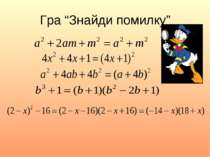Презентація на тему:
Застосування кількох способів розкладання многочленів на множники

Застосування кількох способів розкладання многочленів на множники Київ, СШ № 71, Онуфрієнко Світлана Леонідівна.

Сьогодні на уроці ми повторимо: Різні способи розкладання многочленів на множники Винесення за дужки спільного множника Метод групування Використання формул скороченого множення

1. Знайти цей спільний множник; 2. Винести його за дужки. Щоб розкласти многочлен на множники, винесенням спільного множника за дужки, потрібно:

Алгоритм розкладання многочлена на множники винесенням за дужки спільного множника Знаходимо спільний числовий множник для коефіцієнтів (якщо цілі числа, то шукаємо НСД ); 2. Виносимо за дужки змінну з меншим показником; 12а3b + 8а2b2 = НСД(12;8) = 4 = 4а2b (3а + 2b)

Алгоритм розкладання многочленів на множники способом групування Розбити всі члени многочлена на групи так, щоб після винесення за дужки спільного множника в такій групі в дужках утворилися спільні множники; Винести за дужки спільний множник у кожній групі; Винести за дужки спільний двочленний множник. = (ах + ау) + (5х + 5у) = = а(х + у ) + 5(х + у) = = (х + у)(а + 5) ax + ay + 5x + 5y =

Віднови логічний ланцюжок 3(х + у) – b(х + у) 3х + 3у – bх – bу (х + у)(3 – b) (3х +3у) – (bх + bу) Відповідь: 2 – 4 – 1 – 3

1. Якщо маємо двочлен, то доречно перевірити, чи не можливо використати формулу різниці квадратів або ж формулу різницю (суму) кубів ; 2. Якщо маємо тричлен, то перевірити, чи не можливо його перетворити на квадрат двочлена. Щоб розкласти многочлен на множники, використовуючи формули скороченого множення, потрібно:

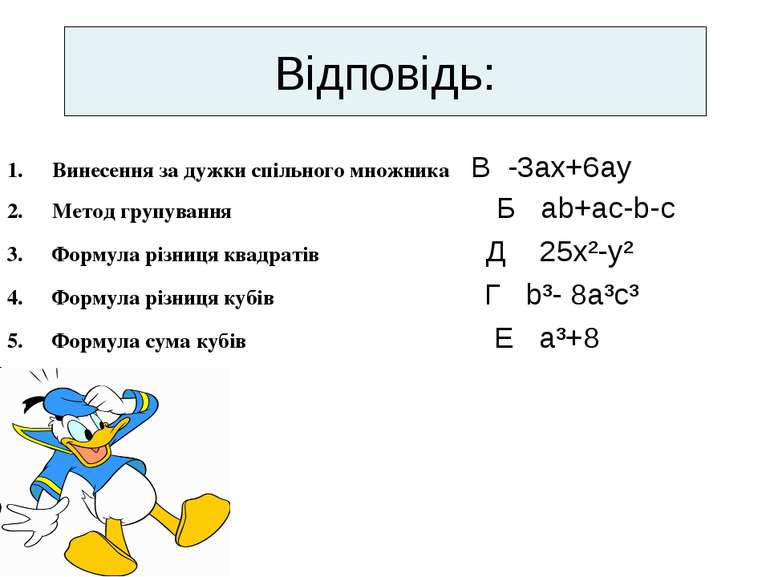
Установіть відповідність між способами розкладання многочленів на множники (1-5) та многочленами, які розкладаються одним із запропонованих способів. Винесення за дужки спільного множника Метод групування Формула різниця квадратів Формула різниця кубів Формула сума кубів А 9a³+b³ Б ab+ac-b-c В -3ax+6ay Г b³- 8a³c³ Д 25x²-y² Е a³+8

Відповідь: Винесення за дужки спільного множника В -3ax+6ay Метод групування Б ab+ac-b-c Формула різниця квадратів Д 25x²-y² Формула різниця кубів Г b³- 8a³c³ Формула сума кубів Е a³+8

Гра “Знайди помилку”

Перевір себе

Самостійна робота

Рекомендації щодо розкладання многочлена на множники, використовуючи одночасно декілька методів: Якщо можливо винести за дужки спільний множник, виконайте це. Поглянь, чи не можливо використати формули: різницю квадратів або різницю (суму) кубів. Якщо не вдається застосувати формули скороченого множення, то спробуйте скористатись методом групування. Коли ви закінчили розклад на множники, корисно перевірити за допомогою множення, чи вірний отриманий вами результат.

Розкладіть многочлен на множники та вкажіть, які способи при цьому використовувались. Приклад 1: 36a6b3-96a4b4+64a2b5 =4a2b3(9a4-4a2b+16b2) =4a2b3(3a2-4b)2 Комбінували два методи: -винесення спільного множника за дужки; - використання формул скороченого множення.

Приклад 2: a2+2ab+b2-c2 =(a2+2ab+b2 ) –c2 =(a+b)2-c2 =(a+b+c)(a+b-c) Комбінували два способи: - групування; - використання формул скороченого множення.

Приклад 3: y3-3y2+6y-8 = (y3-8)-(3y2-6y) =(y-2)(y2+2y+4)-3y(y-2) =(y-2)(y2+2y+4-3y) =(y-2)(y2-y+4) Комбінували три методи: - групування; - використання формул скороченого множення; - винесення за дужки спільного множника.

Підсумок уроку Продовжіть речення: Розкладання многочлена на множники розпочинаю з … Якщо задано тричлен то спробую застосувати… Якщо добуток дорівнює нулю то…

Домашнє завданння: Підручник п.21 Збірник ст.59 №154(6-8), №155(6-8), №156, 157(1)