Презентація на тему:
"Теореми Птолемея Чеви і Менелая"

ТЕОРЕМИ Птолемея Чеви і Менелая Роботу виконав: Дем’янович Тарас Учень 4-А класу Сокальської гімназії Імені Олега Романіва Науковий керівник: Галета Оксана Василівна

Вступ Artes liberales - Вільні, благородні мистецтва (середньовічна назва 7 світських наук: граматики, риторики, діалектики, арифметики, геометрії, астрономії та музики)

Менелай з Александрії та його роботи

Клавдій Птолемей

Чева Джованні

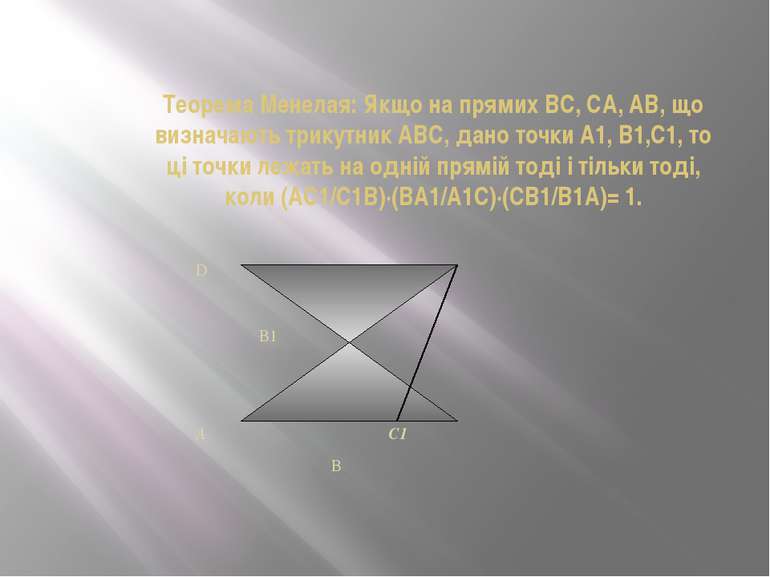
Теорема Менелая: Якщо на прямих ВС, СА, АВ, що визначають трикутник ABC, дано точки А1, В1,С1, то ці точки лежать на одній прямій тоді і тільки тоді, коли (АС1/С1В)∙(ВА1/А1С)∙(СВ1/В1А)= 1. D С В1 А1 А С1 В

В С Е А D Теорема Птолемея: Якщо чотирикутник ABCD вписаний, то AB∙CD+BC∙АD=AC∙BD.

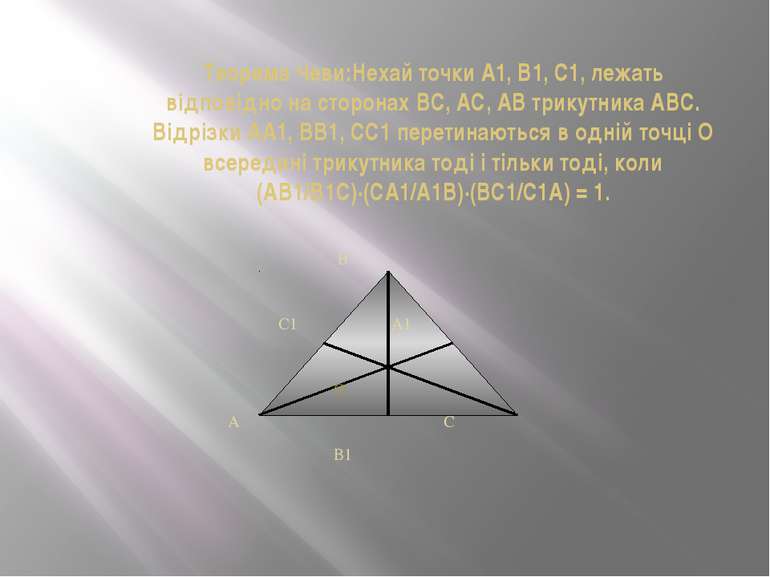
Теорема Чеви:Нехай точки A1, B1, C1, лежать відповідно на сторонах BC, AC, AB трикутника ABC. Відрізки AA1, BB1, CC1 перетинаються в одній точці О всередині трикутника тоді і тільки тоді, коли (AB1/B1C)∙(СA1/A1B)∙(BC1/C1A) = 1. В С1 А1 О А С В1

Висновок У ході роботи я дізнався багато нової і цікавої інформації. Побачив справжню важливість теорем Менелая, Птоломея і Чеви. На перший погляд вони важкі та незрозумілі, але так здається лише на самому початку . Уже через деякий час написання цієї роботи стало для мене задоволенням. З кожною розв’язаною задачею ці теореми все більш захоплювали мене. Моя наукова робота дуже актуальна у наш час, адже 90% студентів закінчивши вищий учбовий заклад не знають теорем Менелая, Чеви та Птоломея. Ці теореми допомагають легко розв’язати багато важливих, корисних, часто досить складних задач. Вони, безперечно, є перлинами стародавньої математики .                                   31