Презентація на тему:
Різні способи доведення теореми про суму внутрішніх кутів опуклого n-кутника

Дудник Н.М.

Теорема Сума кутів будь-якого опуклого многокутника дорівнює або Дудник Н.М.

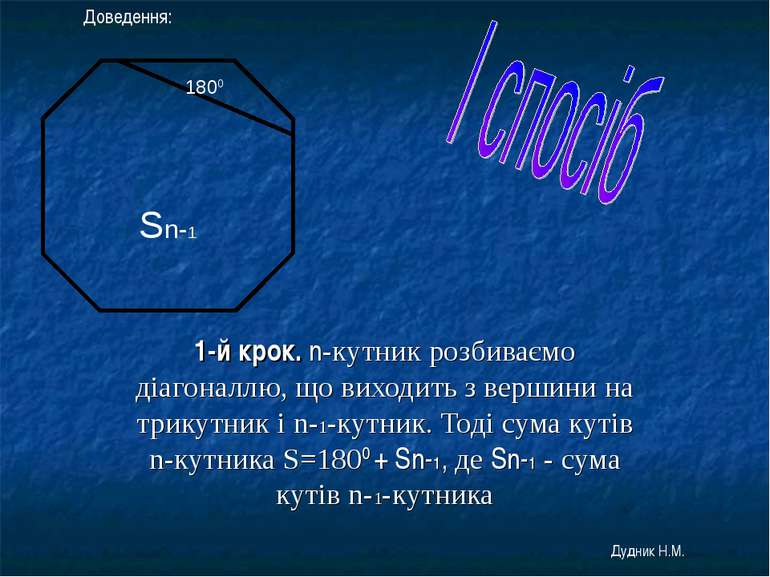
1-й крок. n-кутник розбиваємо діагоналлю, що виходить з вершини на трикутник і n-1-кутник. Тоді сума кутів n-кутника S=1800 + Sn-1, де Sn-1 - сума кутів n-1-кутника Доведення: Дудник Н.М.

2-й крок. Знаходимо Sn-1 розбиваючи n-кутник другою діагоналлю, що виходить з тієї ж вершини многокутника, на трикутник і n-2-кутник. Тоді Sn-1=1800 + Sn-2, Sn=1800+(1800 + Sn-2); Sn=1800 х 2+ Sn-2 Sn-2 Дудник Н.М.

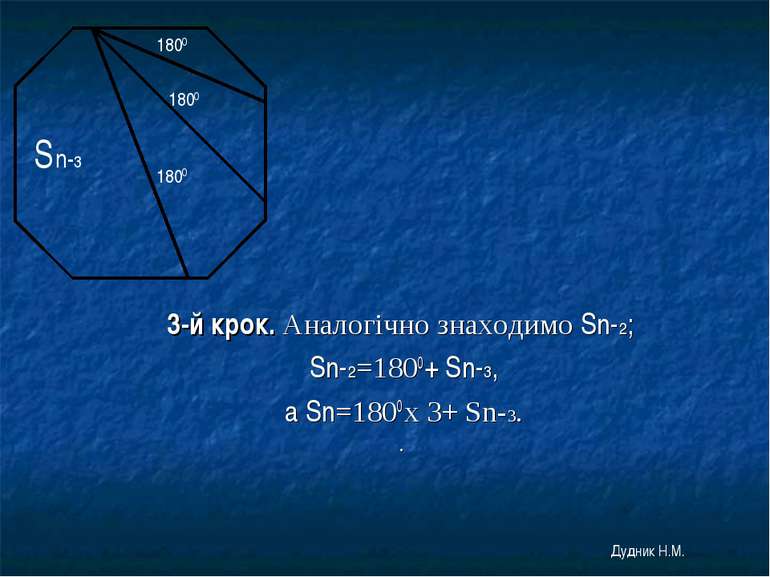
3-й крок. Аналогічно знаходимо Sn-2; Sn-2=1800 + Sn-3, а Sn=1800 х 3+ Sn-3. . 1800 1800 1800 Sn-3 Дудник Н.М.

І так доти, доки останній із многокутників n-3-ю діагоналлю не буде розбитий на 2 трикутники: Sn=1800 х (n-3) + S3; Sn=1800 х (n-3) + 1800 ; Sn=1800 х (n-2). Теорему доведено S3 1800 1800 1800 1800 Дудник Н.М.

Якщо n – кількість сторін многокутника, то n-2 – кількість утворених трикутників. Сума кутів даного многокутника дорівнює сумі кутів усіх цих трикутників: Sn=1800 х (n-2). Теорему доведено. А1 А2 А3 А4 Аn Аn-1 Дудник Н.М.

Нехай О – довільна внутрішня точка опуклого n-кутника. З’єднаємо її з усіма вершинами многокутника. Отримаємо n – трикутників із спільною вершиною в точці О. сума всіх кутів в цій вершині – 3600. Сума кутів всіх трикутників 1800 х n. Тоді 1800 х n =Sn + 3600, де Sn – сума кутів n-кутників. Отже, Sn=1800 х n-3600. Sn=1800 х (n-2). Теорему доведено. А1 А2 А3 А4 Аn Аn-1 Дудник Н.М.

Дудник Н.М.

1. Правильний шестикутник (гексагон) З усіх правильних многокутників правильний шестикутник має найбільшу площу, але найменший периметр. Названу властивість використовують бджоли, будуючи свої соти Дудник Н.М.

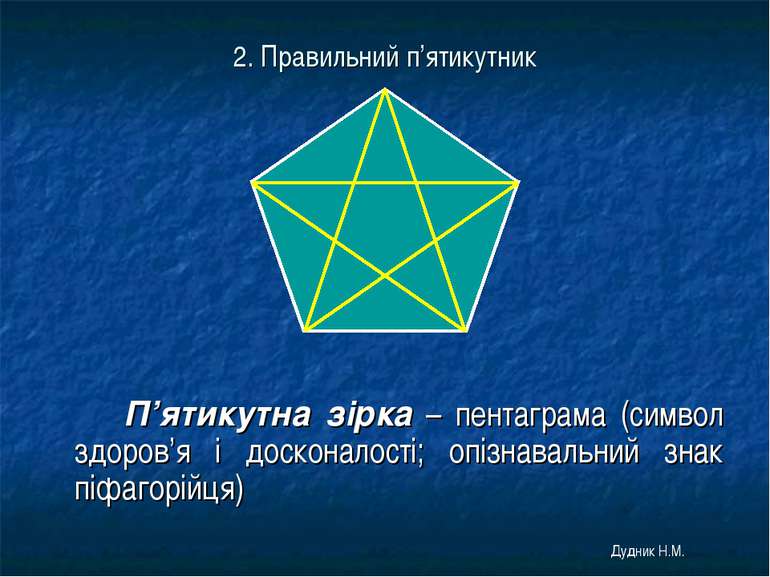
2. Правильний п’ятикутник П’ятикутна зірка – пентаграма (символ здоров’я і досконалості; опізнавальний знак піфагорійця) Дудник Н.М.

Назва військового відомства США не випадкова, бо цей символ має силу, викликає захват і подив з часів піфагорійців, для яких він був знаком. Якщо у п’ятикутнику провести всі п’ять діагоналей, то вони утворюють п’ятикутну зірку – пентаграму. В пентаграмі можна знайти величезну кількість відношень відрізків «золотої» пропорції. Усередині зірки утворюється новий пентагон. Дудник Н.М.

У християнській символіці пентаграма означає Святу Трійцю та подвійну природу Христа (божественну і людську ). У Китаї пентаграма є символом п’яти стихій ( У-Син ) У магії пентаграма одним променем догори символізує людину і є її оберегом, а обернена пентаграма (двома променями догори ) символізує диявола. Пентаграма часто використовувалась у витворах мистецтва. В античному мистецтві відомий закон «золотої чаші», який використовували скульптори й майстри золотих справ. Зрозуміло , що лінійні розміри такої чаші витримують « золоті» пропорції. Дудник Н.М.