Презентація на тему:
"Розв'язування рівнянь з модулями"

Розв'язування рівнянь з модулями Підготував учень 4(8)-Б класу Дем'янович Юрій Вчитель-консультант Гуз Неля Федорівна

Рівняння — аналітичний запис задачі знаходження аргументів, при яких дві задані функції рівні між собою. Методи розв'язання рівнянь були відомі ще у II тисячолітті до н. е. переписувачам стародавнього Єгипту (проте вони не застосовували буквеної символіки). У збережених до наших днів математичних папірусах є не тільки задачі, що приводять до рівнянь першої степені з одним невідомим, а й задачі, що приводять до рівнянь виду aх2 = b (квадратне рівняння). Що таке рівняння

Одним із типів рівнянь є рівняння з модулями це – абсолютна величина в математиці, значення або число незалежно від знака. Абсолютна величина числа записується |x| (іноді mod x) і визначається як додатній квадратний корінь з x². Наприклад, числа -5 і 5 мають однакову абсолютну величину: |5| = |-5| = 5. Такі рівняння і стали об’єктом мого дослідження. Що таке модуль

Мета роботи – дослідити рівняння з модулями і систематизувати способи їх розв’язання Завдання, які ставимо перед собою: - Зібрати рівняння з модулями різної складності - Дослідити різні способи розв’язання рівнянь - Показати практичне застосування модуля Запропонована науково-дослідницька робота надзвичайно актуальна, оскільки розв’язування рівнянь з модулями є проблемної темою для вивчення учнями.

ВИДИ РІВНЯНЬ З МОДУЛЯМИ: Рівняння з модулем Рівняння з двома модулями Рівняння з трьома модулями Рівняння з параметром

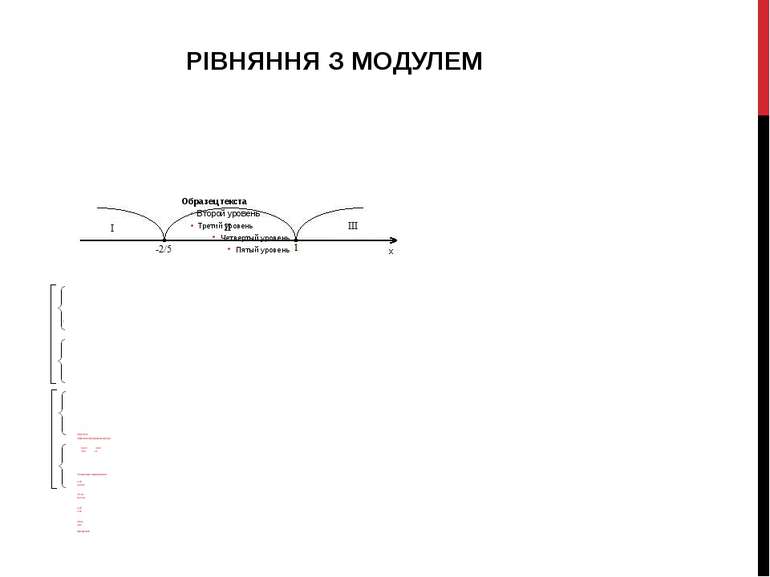
1.3 |5х+2|=3-3х Прирівнюємо під модульний вираз до нуля: 5х+2=0 3-3х=0 х=-2/5 х=1 Отже розглянемо такі сукупності систем: х

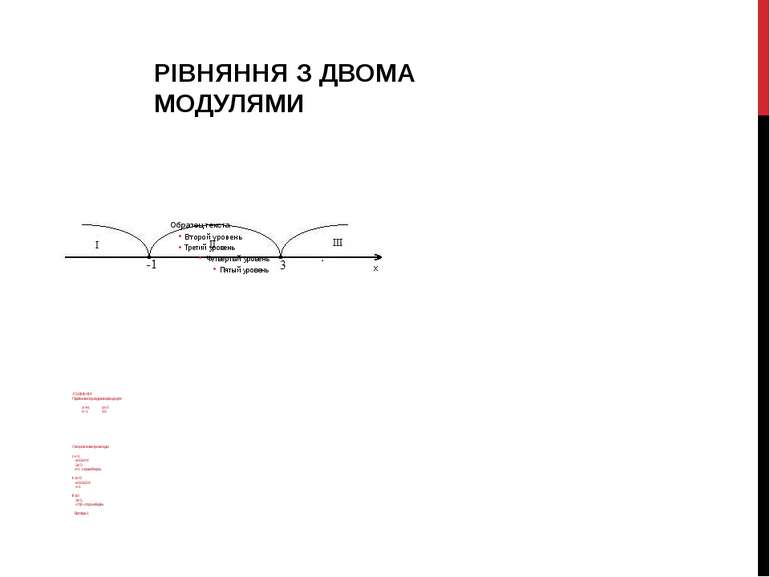
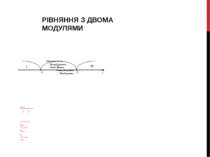
1.7 |х-3|+2|х+1|=4 Прирівнюємо під модульні вирази до нуля: y= x+1 y= x-3 x= -1 x=3 Отже розглянемо три випадки: I. x< -1 -x+3-2x-2= 4 -3x= 3 x= -1 - сторонній корінь ІІ. -1 х

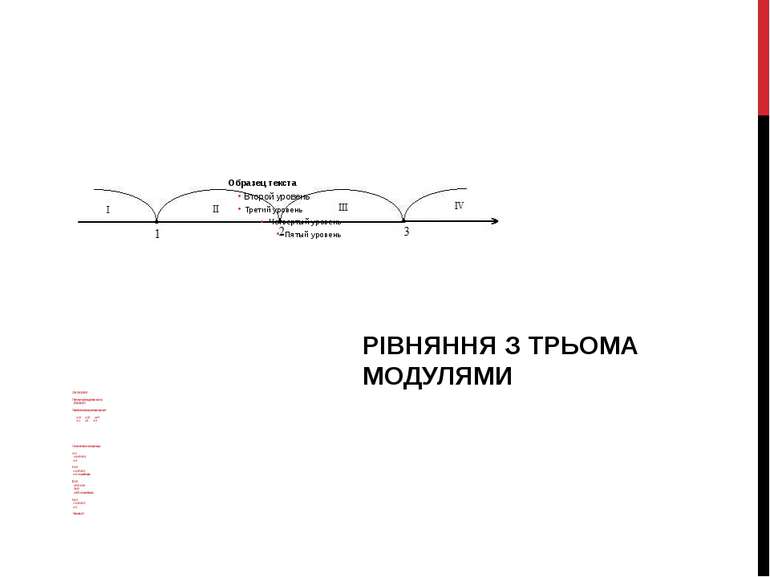
2.0 |х-1|+|х-2|= |х-3|+4 Переносимо усі модулі в ліву частину: |х-1|+|х-2|-|х-3|= 4 Прирівнюємо під модульні вирази до нуля: у= х-1 у= х-2 у= х-3 х= 1 х= 2 х= 3 Отже розглянемо чотири випадки: I. x< 1 -x+1-х+2+х-3= 4 x= -4 ІІ. 1 х

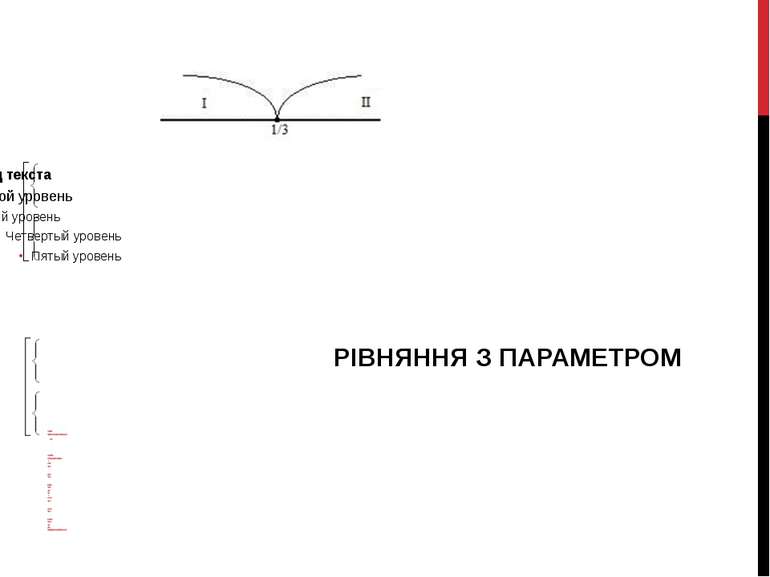
1.4 |х-а|=3х-1 Прирівнюємо під модульний вираз до нуля: х≥1/3 а - параметр Розглянемо дві системи рівнянь: 1 х-а=3х-1 3х-1≥0 х=(1-а)/2 3х-1≥0 (1-а)/2≥1/3 3-3а≥2 -3а≥-1 а 1/3 2 -х+а=3х-1 3х-1≥0 х=(а+1)/4 3х-1≥0 (а+1)/4=1/3 3а+3≥4 3а≥1 а≥1/3 Відповідь: (1-а)/2, якщо а 1/3; (а+1)/4, якщо а>1/3 РІВНЯННЯ З ПАРАМЕТРОМ

В своїй науково-дослідницькій роботі я приділив увагу Кусково-лінійним рівнянням з модулями. На мій погляд вони здаються найскладнішими, а тому їх цікавіше досліджувати. Отже знання теоретичного матеріалу і вивчення основних методів розв’язання задач з модулями допомагає виробити навики розв’язування рівнянь будь-якої складності. Висновок

Дякую за увагу