Презентація на тему:
Рекомендації щодо підготовки учнів до тестування (TIMSS)

Рекомендації щодо підготовки учнів до тестування (TIMSS) МАТЕМАТИКА

Загальні рекомендації У дослідженні значна увага приділяється навчальному матеріалу з математики, що вивчається у 5-6 класах. Отже, потрібно повторити: правила дій з числами, особливо з дробовими перетворення алгебраїчних виразів, застосування властивостей пропорції до розв’язування лінійних рівнянь

еквівалентність математичних структур (запис числа у вигляді звичайного, десяткового дробу або відсотків, рівність геометричних фігур) масштаб використання креслярських інструментів, перехід між одиницями вимірювання, округлення результату

опорні геометричні факти (сума кутів трикутника, властивості суміжних і вертикальних кутів, рівність трикутників, формули обчислення геометричних величин і ін.) належність математичного об’єкта до того чи іншого класу, упорядковування чисел і фігур згідно їхніх властивостей отримання інформації з графіків, таблиць, діаграм; представлення результатів аналізу інформації у вигляді графіків, таблиць, діаграм, перехід від однієї інтерпретації до іншої

Орієнтувати учнів на обов’язкове прочитування текстів завдань, вирішення їх як життєвих ситуацій, застосовуючи насамперед логічне мислення і власний досвід. Запевнити, що для розв’язування таких завдань цілком вистачить наявних в учнів знань Якщо учень не розуміє умову завдання, краще його пропустити і повернутися пізніше

До виконання завдань закритого типу доцільно також застосовувати методи “виключення неможливого результату” і “прикидки результату” Якщо учень не знає чи не впевнений у виборі вірної відповіді до завдання закритого типу, порадити інтуїтивно обрати відповідь, адже навіть тоді ймовірність правильного результату складає 25 %

Основні теми змістових вимірів з математики (8 клас)

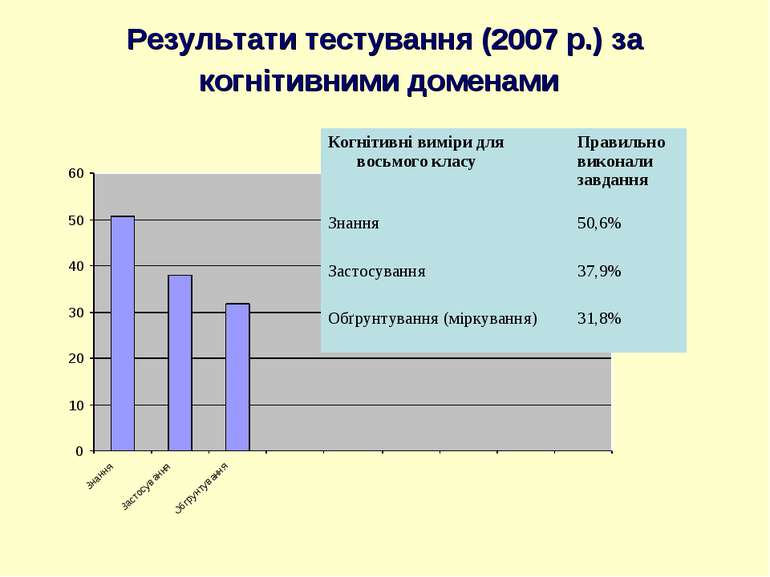
Вимір „Знання” Учні мають виявити вміння: пригадувати точні положення про факти, співвідношення й поняття математики; володіти термінологією, фактами, символікою, поняттєвими одиницями та процедурами, одиницями вимірювання; розпізнавати математичні об’єкти, геометричні фігури, числа та вирази; математичні структури, які є еквівалентними (наприклад: записи дробу у вигляді простого чи десяткового дробу або процентів, по-різному орієнтованих рівних геометричних фігур тощо) здійснювати обчислення числових виразів на додавання, віднімання, множення й ділення цілих чисел, простих і десяткових дробів; з наближеними числами; виконувати стандартні алгебраїчні перетворення виразів; використовувати вимірювальні прилади, відповідні одиниці вимірювання і округлювати результати вимірювання; класифікувати (впорядковувати) об’єкти (геометричні фігури, числа, вирази) за спільними властивостями; зчитувати інформацію з графіків, таблиць, діаграм, різних шкал.

Вимір „Застосування”. Учні мають виявити вміння: вибирати відповідний відомий алгоритм або метод розв’язування (обчислення); представляти математичну інформацію та дані у вигляді схем, таблиць, діаграм, графіків; еквіваленти для заданих математичних співвідношень; моделювати розв’язування стандартної задачі ( наприклад, складати рівняння або графік тощо); виконувати послідовність математичних інструкцій, побудову зображення геометричної фігури за заданими параметрами; розв’язувати стандартні завдання на: порівняння даних у різних форматах; використання даних з діаграм, таблиць, графіків, карт, геометричних властивостей для розв’язування стандартних задач.

Вимір „Обґрунтування ”. Учні мають виявити вміння: аналізувати, тобто визначати, описувати та використовувати зв’язки між об’єктами (змінними); розбивати геометричні фігури на частини для пошуку розв’язання задачі; зображати розгортку незнайомої геометричної фігури; уявляти перетворення геометричних фігур; робити обґрунтовані висновки із даної інформації; узагальнювати – розширювати галузь застосування математичного твердження або розв’язування задачі шляхом переформулювання тверджень умови у більш загальних термінах; синтезувати (об’єднувати) – комбінувати твердження, процедури, пов’язувати математичні поняття для встановлення результату та результати для отримання більш загальних висновків; знаходити зв’язки між різними елементами знання, схожими представленнями; пояснювати, тобто надавати пояснення (доведення) справедливості або хибності тверджень, посилаючись на математичні факти; розв’язувати нестандартні задачі – задачі на застосування математичних знань в незнайомих або складних контекстах (задачах з математичним змістом або задачах пов’язаних з повсякденним життям)

Результати виконання завдань (2007 р.) за змістовим доменами

Результати тестування (2007 р.) за когнітивними доменами

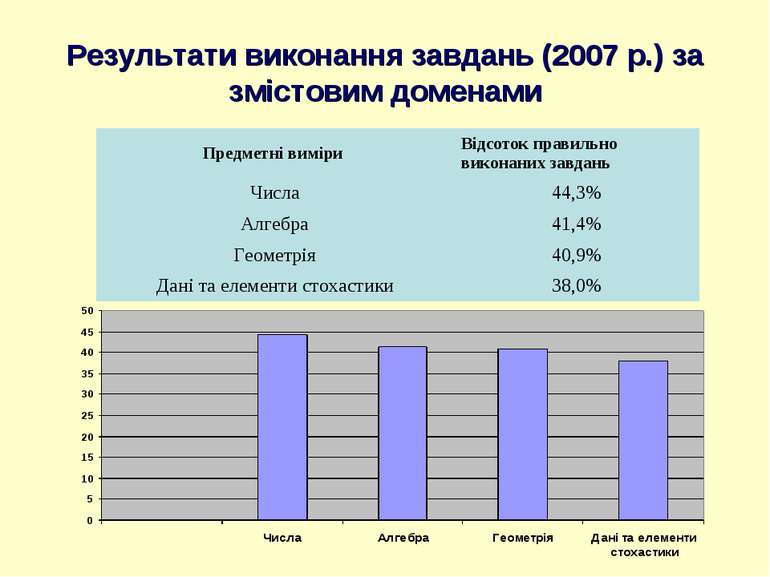
Результати виконання завдань за змістовим напрямом “Числа” (2007 рік) Найкращий результат (близько 70%) виконання завдань, що передбачають: порівняння натуральних чисел, розуміння звичайного дробу, читання і запис десяткового дробу, додавання десяткових дробів з різною кількістю знаків після коми, ділення і множення десятого дробу на число; множення десяткових дробів на 10n, обчислення відсотка від числа

Дещо нижчий результат (близько 50%) учні отримали за вміння виконувати дії з числами з тем: розклад числа на прості множники; знаходження невідомого множника за добутком і іншим множником; знаходження діленого за дільником і часткою; дії з від’ємними числами; розміщення натуральних чисел на числовій осі; зведення дробів до спільного знаменника; порівняння звичайних дробів; знаходження дробу від числа; обчислення добутку десяткового і звичайного дробів; округлення десяткових дробів; основна властивість дробу; пряма пропорційна залежність; знаходження числа за його відсотками

Завдання на запис десяткового дробу в вигляді звичайного і на додавання десяткових дробів правильно виконали лише 24,3% учнів

Серед завдань проекту є завдання на встановлення закономірностей числових послідовностей. Такі завдання потребують від учнів розуміння способів утворення числових послідовностей, а не знання складних теоретичних відомостей

Найпроблемнішими для учнів у темі „дії з числами” виявилися задачі нестандартного формулювання умови, задачі практичного спрямування

Найменша кількість учнів (близько 10%-25%) правильно виконали завдання на: порівняння найменованих величин; перехід між одиницями виміру і їх округлення; перетворення мішаного числа у десятковий дріб; використання властивостей чисел та дії з ними для розв’язування задач

Найкращий результат (близько 65% - 75%) отримано за завдання, що передбачають: уміння пояснювати алгебраїчні вирази (із цілими коефіцієнтами); зведення подібних доданків з цілими числовими коефіцієнтами; розкриття дужок, якщо перед дужкою стоїть знак „+”; позначення точки на координатній площині за її координатами; порівняння значення ординат двох точок за їх розміщенням відносно вісі абсцис (без масштабних поділок на координатних осях) Результати виконання завдань за змістовим напрямом “Алгебра” (2007 рік)

Дещо нижчий результат (близько 50%) отримано з вимірів: використання алгебраїчних символів для представлення найпростіших математичних ситуацій; визначення координат точки перетину двох даних графічних залежностей; визначення ординати точки графічної залежності за її абсцисою; розв’язування найпростіших лінійних рівнянь; визначення ціни позначки кругової шкали та значення, що показує пристрій із такою шкалою

Найменша кількість учнів (близько 10%-25%) правильно виконали завдання на: зведення подібних доданків з дробовими числовими коефіцієнтами; розкриття дужок, якщо перед дужкою стоїть знак „ - ”; знаходження невідомого, що міститься у знаменнику пропорції; використання графічної залежності між величинами для обчислення певних величин (середньої продуктивності, найбільшої продуктивності тощо); розв’язування задач на складання алгебраїчних співвідношень (більше ніж на 1-2 логічні кроки); обчислення значення алгебраїчних виразів, що описують практичні ситуації; визначення закономірностей послідовностей, якщо їх задано не чисельно, а графічно (геометричними фігурами)

Найкращі результати отримано за завдання на просторову уяву (пов’язані з дво- і тривимірними об’єктами) – близько 60% Найважчими для учнів були завдання, що вимагали розкласти задану фігуру на складові, близько 13% правильних відповідей, і завдання на просторову уяву та алгебраїчне моделювання Результати виконання завдань за змістовим напрямом “Геометрія” (2007 рік)

Значна частина учнів не знає, що сума кутів трикутника дорівнює 1800, або не вміє використовувати цей опорний факт

Завдання правильно розв’язали лише 28% учнів

Завдання на властивість суміжних кутів розв’язали лише 35,0% учнів

Завдання виконали близько 40 % учнів

Найкращий результат отримано при вимірюванні вміння учнів зчитувати дані з таблиць і діаграм, особливо стовпчастих діаграм Найгірший результат, близько 10% правильних відповідей, отримано при вимірюванні здатності учнів аналізувати представлені дані у вигляді таблиць або діаграм і робити висновки. Основна причина помилок – неправильне використання масштабу Результати виконання завдань за змістовим напрямом “Дані та елементи стохастики ”

Завдання на обчислення ймовірностей конкретних подій (один логічний крок) правильно розв’язали близько 50% учнів. Завдання на розуміння поняття ймовірності, коли треба було оцінити, яка подія імовірніша або як зміниться ймовірність події, якщо зміниться множина значень випадкової величини правильно виконували близько 40% учнів. Хоча ця тема також не вивчається учнями 8-х класів.