Презентація на тему:
ПЛОЩА

Поняття «площа» виникло із розгляду задач практичного змісту такого типу «Скільки зерна потрібно мати для засіву на даному полі?» «Скільки плиток паркету потрібно для того,щоб скласти підлогу в кімнаті?» Подібно до того як при вимірюванні відрізків ,за одиничний відрізок можна було отримати будь-який відрізок так і при вимірюванні площ за одиниці вимірювання можна брати площу будь-якого квадрату,сторона якого рівна стандартній одиниці довжини : см, дм , м, км. Вони називаються : дм 2 см 2 , дм 2 , м 2 , км 2 . Загально відомі такі міри вимірювання площі : ар, гектар , якими користуються для вимірювання площ земельних ділянок. За одиницю вимірювання площі можна прийняти не тільки площу квадрата . але і площу будь - якої іншої фігури .

Подекуди існували доволі оригінальні міри відстані на землі: кидь ( Харківщина), палку закинути  (Полісся), довержей ( Закарпаття), що означає відстань, на яку можна закинути камінець, грудку землі, палицю. На Полтавщині була відома й така одиниця, як приг ( близько одного сажня), утворювався при стрибанні з палицею. Популярною мірою була гона, при чому розділяли добру гону ( 120 сажнів), середню (60) і малу (30). Для ретельнішого обчислення землі до різних одиниць додавали гаки, величина яких коливалася від чверті до цілої гони.

Українські селяни користувалися доволі поширеними народними способами виміру земельних ділянок. За основу його бралася площа прямокутника з розмірами 30 на 80 або 40 на 60 сажнів. Вживалися також офіційні одиниці виміру – десятина, морг тощо. Побутували і давні народні міри – день, опруг, різа, лан, півланок, одріз, клітка тощо.  Деякі з них означали кількість витраченого часу на обробіток певної ділянки або кількість зібраного урожаю на певній площі.

При вимірюванні сипких одиниць теж користувалися народними одиницями. Зокрема, зерно міряли міркою ( посудиною в пуд або в півпуда вагою), лантухами ( 5 пудів). На Поділлі міряли корцем, який містив 8 пудів. Подекуди користувалися четвериком, що дорівнював 24-26 л. Урожай обчислювали копами ( 60 снопів), хурами та возами. На Закарпатті побутував ферділь – дерев”яна діжка, що вміщала 25 кг зерна. Віком міряли картоплю, кукурудзу, яблука, а вагу м”яса та риби обчислювали офіційною мірою – фунтами (400г) та оками (4 фунти).

Існували одиниці виміру рідких речовин. Так, на Гуцульщині молоко міряли дерев”яним міртуком, галетами ( діжками на 6 – 12 л), децями ( 100г). Воду та горілку повсюдно міряли квартами ( 2 пляшки), гарнцями ( 4 кварти), відрами.

Міри поля У хліборобській практиці потрібно було якось вимірювати поле. Народні міри, що з'явилися у процесі тих чи інших польових робіт, мали досить умовний характер, були надто приблизними. Найбільш поширеною була міра "день орати", чи "день землі", або "на один плуг", тобто величина поля, зорана впродовж дня.

Оскільки продуктивність оранки залежала від типу ґрунту, досконалості знарядь оранки і тяглової сили, то і величини були неоднакові. У Карпатах міра "день орати" становила один морг (0,57 га) землі, а на переважній більшості етнічної території наближалась до одного гектара. На Поліссі побутувала міра "соха", тобто приблизно 0,40 га. Меншою за розміром була "упруга" - третя частина міри "день землі", поширена на Лівобережжі. "Упруги" були ранкові, обідні, вечірні.

Великі площі поля вимірювалися "ланами" (19-25 га), на Поліссі, Волині - "волоками" (21 га), що поділялися на "прути" (1,2-1,5 га). Це були дещо регламентовані міри поля, на відміну від тих, які визначались за виконаною роботою протягом одиниці часу. Існували міри площі за величиною скошеного поля ("день косити"), за кількістю висіяного зерна - "віко" (1/8 га, на яку припадає 25 л зерна для засіву).

На Закарпатті селяни послуговувалися мірою, яка називалася "ділець" ("телека") - величина сільськогосподарських угідь, що забезпечувала прожитковий мінімум для господаря. Сюди належали: садиба, орне поле, луки, пасовисько. Народні виміри виявилися живучими: навіть після запровадження стандартизованих одиниць, таких, як десятина (1 га), морг (0,57 га), гольд (0,48 га), кадастральний гольд (0,57 га), угр (1 га) тощо, селяни використовували давні міри паралельно.

Міри площі У давнину міри площі були найрізноманітнішими: 1.    Десятина — 1,09 га. 2.    Квадратна верста — 1,1 км2, 3.    Квадратний сажень —1,1м2. 4.    Квадратний аршин — 0,5 м2. 5.    Квадратний вершок —19,7 см2. 6.    Квадратний фут — 0,09 м2. 7.    Різа — 3,6 десятин. 8.    Морг — 0,57 га. 9.    Лан — 10 десятин. 10.  Стая — 1,75 морга. 11.  Волок — ЗО моргів. 12.  Ґрунт — 3 загони, загін — 4 морги.      Міри 1—12 використовували у Львівській і Житомирській областях.

У Чернівецькій області використовували міри 13—17: 13.    Пражна — 130 м2. 14.    Фальча — 80 пражин. 15.    Різа — 10 моргів. 16.    Морг — 45 пражин. 17.    Влока — 20 моргів.      На Гуцульщині використовували міри 18—21. Тут терміни вимірів земельних ділянок пов'язували з часом, потрібним для обробки поля: день, упруг, різа. Наприклад, день — площа землі, яку виорює сита пара волів за день, упруг — площа землі, яку виорює пара волів з ранку до обіду. 18.    Різа — 10 моргів. 19.    Лук — 252 сажні2. 20.    Обжа — 2 луки. 21.    Соха — 3 обжі.

Виникнення мір площі у Египті . Соціальна організація Єгипту залежала від універсальної системи мір. Стандартні міри довжини вели своє походження від різних частин людського тіла. Одиницею виміру коротких відстаней, що використовувалася в основному художниками й скульпторами, був фут (стопа). Більшою одиницею довжини був лікоть, що ділився на дві п'яді, шість долонь і 24 пальці. Стандартний лікоть дорівнював 46 сантиметрам, а царський лікоть був на 4 сантиметри більше. Значні відстані вимірялися в ітру, довжина якого становила 5000 ліктів. Царські землеміри при вимірі площі використовували квадрати зі стороною 100 царських ліктів (хет). Стандартною мірою об'єму рідини був хену, що дорівнював приблизно одній третині літру. Основною мірою ваги був дебен, рівний приблизно 90 грамам.

Кв. кілометр ( кв.км.) = 100 000 кв.м . Кв. кілометр ( кв.км.) = 100 гектарів або 10 000 Ар. Ар (а.) = 100 кв. метрів або 10 000 кв. см . Кв . метр ( кв. м. ) = 100 кв. дециметрів Кв. дм. = 100 см 2 М 2 = 10 000 см 2 См 2 = 100 м 2 См 2 = дм 2

Периметр – від грец. «парі» (навколо) і «метро» буквально- обвід, довжина замкненої кривої. Площа – латинське «супердпсиіс» ( поверхня).

Орієнтовні завдання для учнів

Скільки квадратних сантиметрів у кожній фігурі? 1 см

Площу вимірюють за допомогою формули: довжину помножити на ширину.

2. За поданим планом і числовими даними знайди невідомі розміри окремих ділянок та площу.

3. У кожного прямокутника виміряй довжину сторін і обчисли площу.

4. Виміряй площу цих прямокутників . Скажи : у якого із них площа сама більша , а у якого менша?

5. Накресли на папері в клітинку квадрат , в якого площа 4 кв. см. .Яка довжина сторони цього квадрату?Накресли другий прямокутник, у якого така ж площа 4 кв.см. Яка довжина сторони цього прямокутника? 6. За даними малюнків знайди невідомі величини: Площа? Периметр?

Ігри на створення з геометричних фігур образних і сюжетних зображень

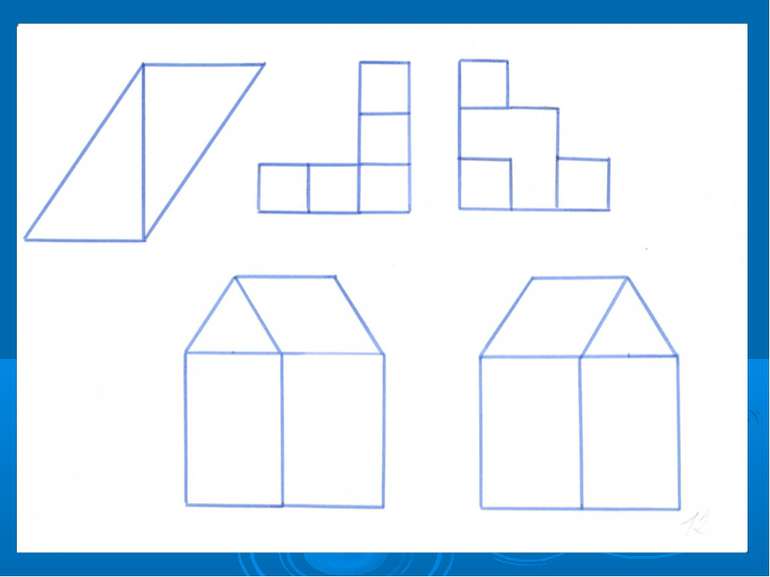
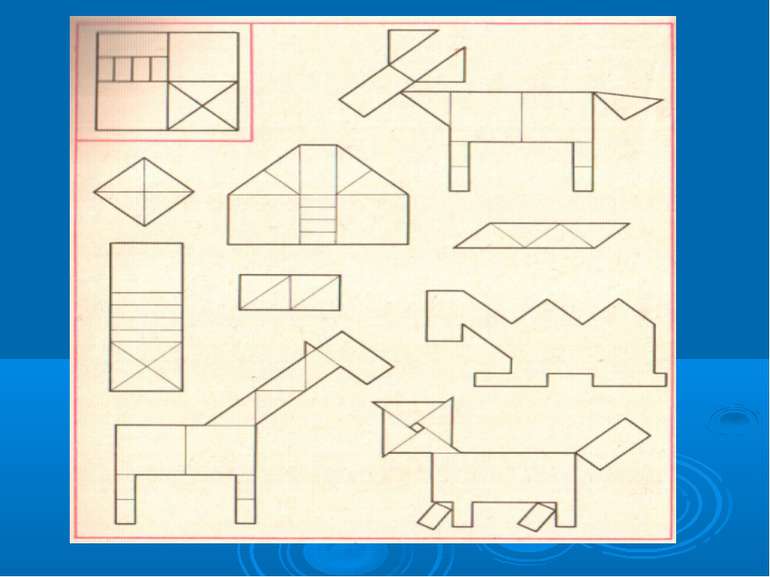
Особливе місце серед математичних розваг займають ігри на складання класних зображень предметів, тварин, птахів, будинків, караблів та інше з спеціальних наборів геометричних фігур. Набори фігур при цьому підбираються не довільно, а являють собою частини розрізаної певним чином фігури: квадрата, прямокутника, круга чи овала. Вони цікаві дітям і дорослим. Дітей захопляє результат – скласти побачене за зразком чи задумане. Вони включають в активну практичну діяльність по підбору способу розміщення фігур з метою створення силуета. Ось деякі з них :

Під час викладання теми «Площі фігур» можна розповісти про те, що обчислення площі або поверхні фігури називають квадратурою. У стародавніх єгиптян квадратура якоїсь фігури зводилась до побудови рівновеликого квадрата. Звідси походить термін «квадратура круга». Цю назву мала одна з відомих задач давнини. Здійснити квадратуру круга означало побудувати за допомогою циркуля та лінійки квадрат, рівновеликий кругу. Цей вираз став синонімом задачі, що не піддається розв'язанню. Ще один спосіб створення проблемних ситуацій — це спонукання учнів до виявлення внутрішніх і міжпредметних зв'язків і зв'язків між явищами.

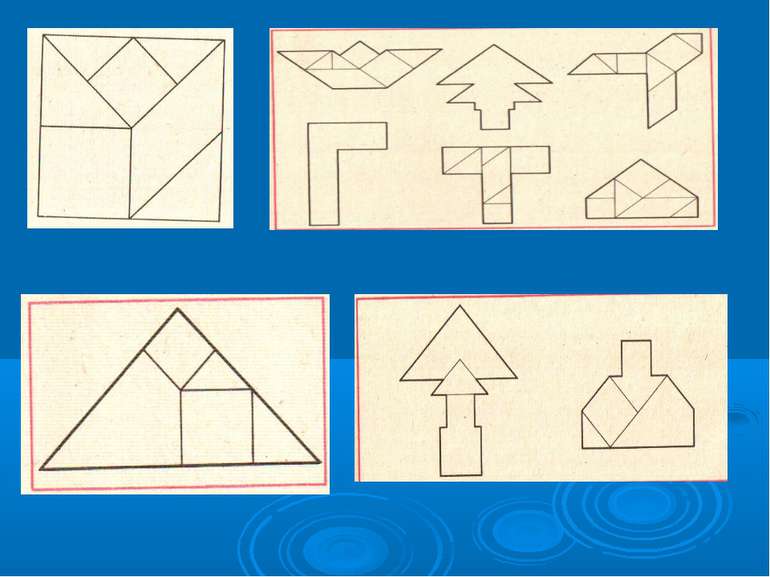
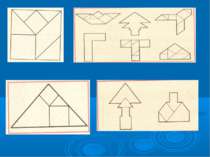
Гра «Танграм» «Танграм» - старовинна китайська гра – головоломка. Вона виникла 4 тисяці років назад. В Китаї гру називають Ші-Чао-Тю-сім хитромудрих фігур. Суть її полягає в складанні з 7 чакстини, одержаних при розрізі певним числом квадрата розміром 8см*8см з пластини квадрат, різних фігур, а також придумування нових. Гра допомагає не лише засвоїти назви геометричних фігур, їх властивості, характерні ознаки, а й практично видозмінювати фігури шляхом розрізу і складання їх з частин. Крім того гра розвиває усидчивость і терпіння, розвивати логіку мислення, геометричну інтуіцію, образну уяву.

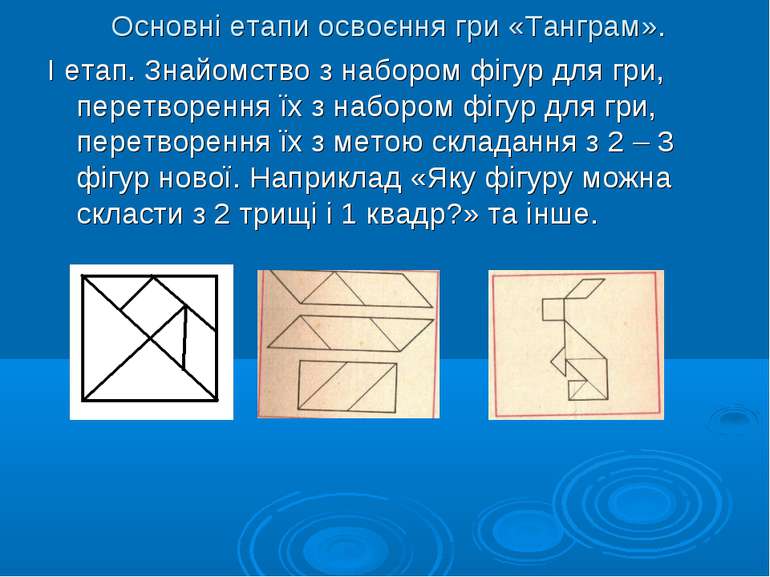
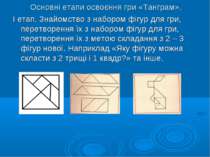
Основні етапи освоєння гри «Танграм». І етап. Знайомство з набором фігур для гри, перетворення їх з набором фігур для гри, перетворення їх з метою складання з 2 – 3 фігур нової. Наприклад «Яку фігуру можна скласти з 2 трищі і 1 квадр?» та інше.

ІІ етап. Складання фігур – силуетів за різними зразками. На цьому етапі діти аналізують запропонований зразок, починаючи з головних частин. За аналізом слідують вправи в складанні фігури, орієнтуючись на зрозок. Зразок не прибирається, діти при потребі можуть звернутись до нього. На послідуючих заняттях, в міру накопичення досліду в складанні фігур, немає потреби дотримуватись цього правила.

З метою розвитку творчості можна запропонувати і більш складні завдання, наприклад, з 2 – 3 однакових наборів фігур до гри «Танграм» скласти фігуру – силует, сюжет як за зразком, так і за власною уявою, задумом.Така робота значно важка.Тому використання зразків з позначенням цифрами місця розташування частин в фігурі – силуеті полегшує задачу. Вказано лише місце розташування фігур, наприклад, маленьких трикутників цифрою 1, а не способів їх розташування (наприклад, в поєднанні з іншими фігурами).

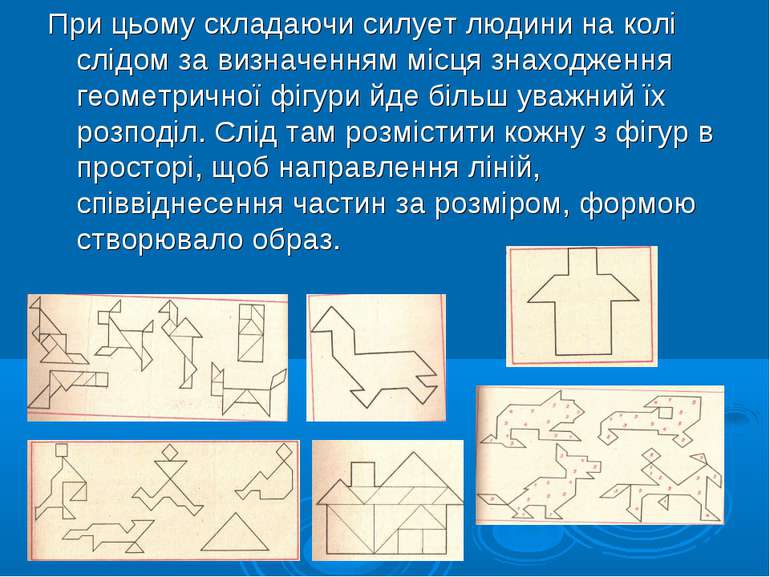
При цьому складаючи силует людини на колі слідом за визначенням місця знаходження геометричної фігури йде більш уважний їх розподіл. Слід там розмістити кожну з фігур в просторі, щоб направлення ліній, співвіднесення частин за розміром, формою створювало образ.

Гра – головоломка «Піфагора» Квадрат розміром 7см*7см розрізається так, що отримається 7 геометричних фігур: 2 різних за розміром квадрата, 2 маленьких трикутника, 2 великих і 1 чотирикутник (паралелограм). Гра розвиває мислення, просторову уяву, винахідливість, смикалку.

Якщо при складанні фігури – силуета за нерозділеним зразком виникають забруднення можна запропонувати зразок, де вказано місце розташування 1-ї і 2-ї частини гри із заданих 7 частин. Останні дитина розмістить самостійно.

«Монгольська гра» Квадрат розміром 10*10см розрізають як показано на рис. В результаті виходить 11 частин: серед них 2 квадрата, 4 трикутника, 5 прямокутника (4 маленьких і 1 великий). При складанні фігур – силуетів використовуються всі частини, приєднуючи одну до одної, не накладаючи одну частину на іншу.

«Колумбове яйце» Овал розміром 15*12см розрізують, як показано на рисунку. В результаті виходить 10 частин: 4 трикутники, 2 фігури, схожі на чотирикутники, одна з сторін яких заокругленої форми, 4 фігури (великі і малі) схожі на трикутник, але з заокругленою однією стороною. Правила гри такі ж, як і в «Монгольській грі». Можна скласти птахів в польоті, пінгвіна, людину, рицарів, воїнів, балерин, коней, лошат і т.д.

Одним з прийомів, що полегшує складання фігури – силуета то нерозчленованому зразку, можна використати кольорову вказівку місця розташування частин. На кожному частину гри наноситься кольорове п’ятно і точно таке ж – на місце розташування цієї частини і силуеті, що складається. Наприклад, маленькі трикутники помічаємо червоним п’ятном, великі – синім, маленькі трикутники з заокругленою стороною – жовтим, великі – зеленим, чотирикутником з заокругленням – чорними. При такому способі складання фігур слід представлять розміщення частини в просторі, місце не розташування вказане.

Математичні цікавинки

Чи знаєте ви , що… Для того,щоб 270 кв.км. Землі покрити шаром туману товщиною 15 метрів , досить одного відра води.

Как измерить площадь? Нет задачи проще! Поглядите-ка сюда : Стали мерки в два ряда , Будто бы солдатики – Ровные квадратики. Чтобы площадь нам узнать , Нужно их пересчитать.

Анаграми Т А К Г Е Р Р И Т П Е М Р Е Щ А Л О П ’’’ща

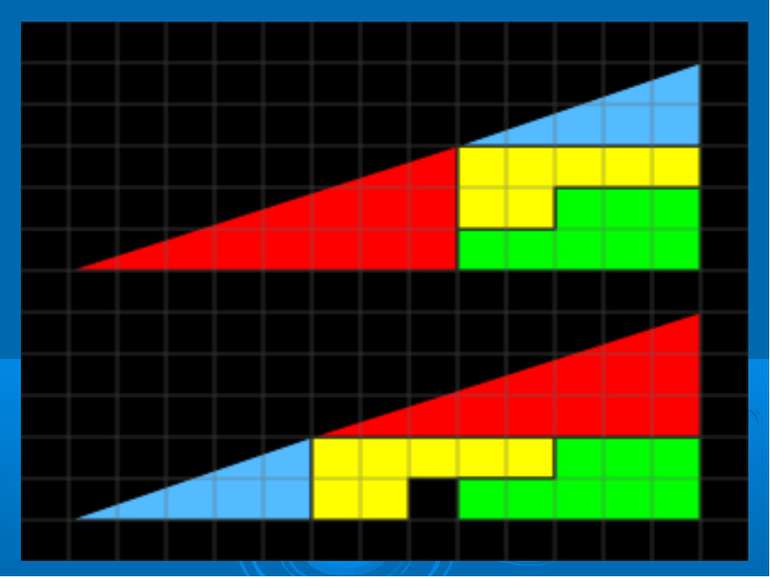
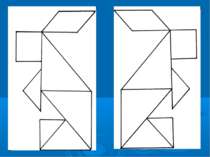
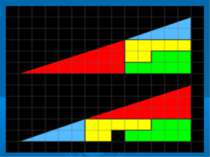
Загадка зниклого квадрата  — це оптична ілюзія, що часто використовується на уроках математики для пояснення властивостей геометричних фігур. Вона зображає дві фігури, складені з одинакових частин, але в різному порядку, на вигляд прямокутні трикутники із катетами відношенням 13 до 5. Але один із них містить прогалину — квадрат 1х1. Згідно з Мартіном Гарднером, головоломку придумав Нью-йоркський фокусник-аматор Поль Керрі у 1953. Відтоді загадка була відома під назвою «Парадокс Керрі», хоча рішення було відоме ще з 1860-х .

Розв'язок : «Гіпотенузи» 13×5 «трикутників» насправді є ламаними лініями,які утворюють паралелограм Ключем до загадки є те, що жодний із 13×5 «трикутників» не має ту ж саму площу, що й площа їх складових.

Сумарна площа чотирьох фігур (жовтої, червоної, синьої та зеленої) становить 32 одиниці площі, але довжини сторін трикутників 13 та 5, що відповідно становить 32,5 квадратних одиниць. Відношення катетів синього трикутника 5:2, а червоного 8:3. За ознакою подібності прямокутних трикутників випливає що ці трикутники не подібні, а значить мають різні відповідні гострі кути. Отже, видимі складені «гіпотенузи» великих «трикутників», насправді є ламаними. Кут нахилу гіпотенуз червоного та синього трикутників до гіпотенузи 13×5 трикутника дуже малий і його важко помітити неозброєним оком. Але якщо приглядітись, то видно, що точка стику гіпотенуз червоного та синього трикутників, формує тупий кут, що трішки вигнутий вгору (назовні) нижнього «трикутника» і тупий кут вигнутий вниз (всередину) верхнього «трикутника». Якщо накласти «гіпотенузи» обох фігур, то утвориться паралелограм, площею рівною одному квадратику. Довжини сторін фігур з даної задачі (2, 3, 5, 8, 13) є послідовними числами Фібоначчі.

ОДИНИЦІ ВИМІРЮВАННЯ ВЕЛИЧИН У ЦІКАВИХ ЗАДАЧАХ І ЗАВДАННЯХ

Маємо 8 монет однакової вартості, серед них одна фальшива. Фальшива монета трохи легша за інші. Як визначити фальшиву монету двома зважуваннями на терезах з вдома шальками без гирьок? (Відповідь: Перший раз покласти на терези по три монети. Якщо монети будуть у рівновазі, то фальшива монета буде серед останніх. Якщо терези не будуть у рівновазі, то фальшива монета у вищі шальці. Взяти монети з вищої шальки і дві з них покласти на шальки). Котра зараз година, якщо частина доби, яка залишилася, у 2 рази менша за ту, що минула? (Відповідь: 4 год. дня). Батькові 32 роки, одному його синові 8 років, а другому - 6 років. Через скільки років вік батька дорівнюватиме сумі років обох синів? Поясни відповідь. (Відповідь: 8 + 6 = 14; 32 - 14 = 18. Через вісімнадцять років). Швидкість течії річки 6 км за год. Власна швидкість катера - 18 км за год. На скільки швидкість руху катера за течією буде більша, ніж проти течії? (Розв'яжи задачу однією дією). (Відповідь: 6 + 6 = 12 (км за год).

Ділянку землі прямокутної форми шириною 18 км і площею 576 м2 треба огородити дротом у 3 ряди. Скільки знадобиться дроту? (Відповідь: 300 м). Два велосипеди виїхали одночасно з міста до табору. Один їхав зі швидкістю 10 км/год., а другий - 13 км/год. Через 2 год. другий велосипедист проколов камеру, тому далі рухався пішки зі швидкістю 4 км/год. на якій відстані від міста перший велосипедист дожене другого? (Відповідь: на відстані 30 км). Маса 9 кальок така сама, як маса 2 кубиків і 2 шайб. Шайба у 2 рази легша, ніж кубик. Скільки кульок треба взяти, щоб їх маса дорівнювала масі 1 кубіка? (Відповідь: Маса одного кубика дорівнює масі трьох кульок). За 4 хв колоду розпиляли на півметровки, причому кожне розпилювання займало хвилину. Знайди довжину колоди. (Відповідь: Всього буде 5 півметрівок, отже, довжина колоди 2 м 50 см). У кімнаті є годинник. Він відбиває цілі години. Скільки ударів на добу робить цей годинник? (Відповідь: 180 ударів).

У пакеті 9 кг крупів. За допомогою терезів з гирями 50 г і 200 г треба розкласти ці крупи у два пакети: в один - 2 кг, в другий - 7 кг. Спробуй це зробити за три зважування. (Відповідь: 9 кг : 2 = 4 кг 500 г (перше зважування); 4 кг 500 г : 2 = 2 кг 250 г (друге зважування); 2 кг 250 г - (200 г + 50 г) = 2 кг (третє зважування). У двох банках було однакове число літрів води. Коли з першого взяли ? води, а з другого 240 л, то в обох банках залишилась однакова кількість води. Скільки літрів води було в банках разом? (Відповідь: 1920 л).

Методичні розробки по площі

Тема уроку: Ознайомлення із поняттям площі. Мета: ознайомити учнів із поняттям площі; формувати вміння порівнювати площі фігур, вирізаних із кольорового картону, зображених в зошитах чи на дошці, фігур, що їх оточують; сприяти розвитку порівняння, аналізу у дітей; корегувати недоліки просторової уяви, окоміру учнів Обладнання: геометричні фігури, вирізані із кольорового картону, таблиця із зображенням фігур, нелінований папір. Хід уроку. 1. Організація учнів на урок. Перевірити готовність учнів до уроку геометрії,зосередити увагу учнів та налаштувати на роботу грою: „Впізнай і назви лінії на таблиці"

2. Актуалізація опорних знань учнів. Які лінії знаєте? (Ми знаємо прямі, криві, ламані лінії); Виберіть із таблиці тільки прямі лінії; Яка це пряма лінія? (Що не має ні початку, ні кінця); А відрізок - це пряма лінія? (Так, відрізок - це частика прямої, що має початок і має кінець); Які ще частини прямої ви бачите на таблиці? (промені); Які ще лінії є на таблиці? (Криві і ламані лінії); Покажіть всі ламані лінії, з чого вони складаються? ((2), (13), (14) - ламані лінії, складаються з відрізків, які послідовно з'єднані між собою);

Покажіть всі криві лінії. ((3), (9), (15)); Чим відрізняється фігура за номером (7) від фігури за номером (9)? (Фігура (9) - крива лінія (ободок), коло, а (7) - круг - частина площини, що обмежена колом); Чи відрізняється фігура (4) від фігури (14)? ((4) - трикутник, частина площини, яка обмежена замкненою ламаною лінією із 3-х відрізків, а (14) - замкнена ламана лінія). 3. Повідомлення теми, мети уроку. Вчитель показує на таблиці фігуру за номером (11) і повідомляє, що частину площини, яка обмежена замкненою лінією із п'яти відрізків ще називаються площею п'ятикутника. Тоді вчитель показує частину площини трикутника, прямокутника (на таблиці) і повідомляє, що сьогодні ми ознайомимось із поняттям площі. Запишіть тему уроку в зошитах.

4. Повідомлення нового матеріалу. Вчитель бере в руки 2 чотирикутники різної величини і просить взяти учнів такі ж чотирикутники. - Покажіть частину площини малого і частину площини великого чотирикутника та їх межу. - Як порівняти ці чотирикутники? (Шляхом накладання) Діти порівнюють чотирикутники, а вчитель повідомляє: - В такому разі говорять, що площа малого чотирикутника менша від площі великого. 5.Первинне закріплення нового матеріалу. Виберіть із фігур, що знаходиться у вас на парті, круг та трикутник. Покажіть частину площини круга, частину площини трикутника (їх межу). Порівняйте площі фігур. Що можна сказати про їх площу? (Площа трикутника менша від площі круга) Форму якої фігури вам нагадує кришка парти? Форму якої фігури нагадує вам дошка? Покажіть частину площини кришки парти. Покажіть частину площини дошки. - Порівняйте площі кришки, парти і дошки.

6. Виконання практичної операції. Робота з підручником. Побудуйте в зошитах квадрат із стороною 3 см та прямокутник із сторонами 3 см і 5 см. Площа якої фігури більша і чому? Чим скористаємось для побудови фігур? (Креслярський косинець, олівець, лінійка) Для чого нам креслярський косинець? (Для побудови прямих кутів) Що ми називаємо прямокутником? (Прямокутник - це паралелограм, у якого всі кути прямі) Що ми називаємо квадратом? (Квадрат - це прямокутник, у якого всі сторони рівні) Чим відрізняється квадрат від прямокутника? (У квадрата всі сторони рівні, а у прямокутника тільки протилежні сторони рівні) Один учень побудову здійснює на дошці. - Якими мірами довжини користуємось при побудові на дошці? (Дециметрами) Чому? (Щоб збільшити зображення) У скільки разів? (У 10 разів)Після побудови: Площа якої фігури більша? (площа прямокутника) Чому? (Прямокутник більший за квадрат) 7.Повторення, узагальнення і систематизація знань учнів. З чим ознайомимось сьогодні на уроці? (Із поняттям площі фігури) Порівняйте площу підлоги в класі і площу стелі. Форму якої фігури вони нагадують? (Прямокутника) - То яка фігура займає більшу площу? (Підлога і стеля займають однакову площу, вони рівні) Завдання на нелінованому папері.

Побудуйте круг радіусом 3 см, та квадрат із стороною 6 см. Вирізавши їх, порівняйте площу фігур. Чим скористаєтесь для побудови круга? (Циркулем, олівцем, лінійкою) Чим скористаєтесь для побудови квадрата? (Креслярським косинцем, лінійкою, олівцем) Що займає більшу площу спортзал чи стадіон? (Стадіон) Чому? (Стадіон більший від спортзалу) Що займає меншу площу Чернівці чи Україна? Чому? Домашнє завдання (кожному учневі дати завдання на виготовлення певної фігури з кольорового картону) Підведення підсумків уроку. Що навчилися порівнювати на уроці? (Площу фігур) Як порівняти площу фігур? (Перевірити, яка фігура більша чи менша) Порівняйте площу обгортки зошита і площу обкладинки книги. Площу стенду і площу підвіконника. Площу, яку займає подвір'я школи і площу, яку займає наша вулиця. Мотивація оцінок.

Тема: Правила обчислення площі прямокутника та його застосування. Мета: Формувати у дітей вміння обмалювати площу прямокутника. Вчити розв'язувати задачі. Розвивати кмітливість, логічне мислення. Виховувати працьовитість, самостійність. Обладнання: моделі прямокутників, прямокутників поділених на квадратні сентименти. Хід уроку І.Організаційна частина. Продзвенів уже дзвінок Всіх покликав на урок То ж давайте привітаймось Добрий день. ІІ. Актуалізація опорних знань, умінь і навичок. Усний рахунок - Наш урок ми розпочнемо з усного рахунку. Я вам буду показувати карточки з прикладами, а ви усно будете їх розв'язувати і казати лише відповідь. 0:200=(0) 350650=(7) 100 6= 600 (який знак потрібно поставити) 100:20=6 (чи правильно розв'язаний приклад) 500:0-0 (чи правильно розв'язаний приклад) Каліграфічна хвилинка. - А зараз ми напишемо цифру 5. Сядьте всі рівненько, випрямте свої спинки. Якщо сядете красиво То напишете на диво Чисто, рівно і красиво Раз, два, три, чотири, п'ять.

Починаємо писать. Хто написав відкладіть ручки Математичний диктант - А зараз ми напишемо математичний диктант. Будьте дуже уважними, я буду читати один раз. а) 80 зменшити в 40 раз б) сума чисел 30 і 50 зменшити в 20 раз в) добуток чисел 15 і збільшити в 2 рази г) сума чисел 10 і 6 збільшити у 5 раз д) різницю чисел 80 і 20 зменшити в 2 рази е) 2 збільшити в 30 різ Перевірка математичного диктанту А зараз прочитайте перші 3 відповіді. Яка фігура має більшу площу? Хто прочитає наступні три відповіді? Що таке квадратний сантиметр. ІІІ. Оголошення теми та завдань уроку. Вступна бесіда. На минулому уроці ми навчилися обчислювати площу фігури, підраховуючи число квадратів, площею 1 см2. Однак цей спосіб не завжди зручний. Наприклад, коли треба знайти площу ділянки поля. Для знаходження площі прямокутника існує правило, сьогодні ми з ним ознайомимося. Ознайомлення. Знайдіть площу прямокутників, зображених на малюнках. Виміряємо його довжину і ширину (8 см і 1 см) Розіб'ємо на квадратні сантиметри і порахуємо. Їх є 8, тобто стільки, скільки лінійних сентиментів є в довжині. Як зручніше порахувати число квадратних сантиметрів у цьому прямокутнику? Нам (з попереднього) відомо, що в одному ряду є 8 см2, а якщо таких рядів два, то 8 х 2 = 16 (см2)

Самостійно знайдіть площу третього прямокутника. Як ви знаходили? 3 ряди по 8, то 8х3=24 (см2), або 8 стовпців по 3, то 3х9=24 (см2). Чи потрібно розвивати прямокутник на квадрати? Що означають числа 3 і 8? Якою дією ми знаходили площу? Що треба зробити, щоб знайти площу прямокутника? Правило: щоб обчислити площу прямокутника, треба визначити його довжину і ширину та знайти добуток цих чисел. ІV. Обчислення площі прямокутника. Розглядають задачі двох видів: дано сторони прямокутника, знайти його площу; Фізкультхвилинка. А зараз ми з вами трохи відпочинемо. Сонце спить Сонце встало, потягнулось Загримів грім Сонце заховалося, Трава низенька - низенька А дерева високі - високі Вітер дерева колише - гойдає.

Послухайте уважно задачу: Мама купила килим - картину, довжина якого 4 м, а ширина 2 м. Визначте площу цього килима. Аналіз умови Що купила мама? Яка довжина килима? Яке запитання до задачі? Складання плану Яку форму має килим? Пригадайте, як знайти площу прямокутника? Чи відома нам довжина? А - ширина? Отже, що треба зробити? Запишіть в зошити? 4 х 2 = 8 (кв.м) - площа килима V. Підсумок уроку. Про що ми говорили на сьогоднішньому році? Як знайти площу прямокутника? VІ. Домашнє завдання. На домашнє завдання вам буде накреслити два довільних прямокутника, виміряти їх довжину і ширину, а потім знайти площу. А також вивчити правило, як знайти площу прямокутника. На цьому наш уроку закінчується.

Висновок

З поняттям “площа” діти знайомляться в 3 класі трирічної початкової школи або в 4 класі чотирирічної початкової школи. Методика роботи над площею фігури має багато спільного з роботою на довжиною відрізка. Насамперед площу розглядають як властивість плоских предметів серед інших їхніх властивостей. Під час опрацювання цієї теми у третьокласників (четвертокласників) виникають деякі утруднення. Переходячи до квадратних одиниць вимірювання, діти постають перед незвичним фактом: назви їх схожі на назви лінійних мір, а співвідношення різні. Це і перешкоджає швидкому засвоєнню нових відношень. Учні часто припускаються помилок. Завдання вчителя і полягає в тому, щоб у доступній формі не тільки ознайомити третьокласників (четвертокласників) з квадратними мірами, а й нагромадити досвід таких вимірювань, закріпити набуті дітьми знання, уміння і навички.

Поглиблюючи поняття площі та розширюючи уявлення дітей про одиниці вимірювання, матеріал варто подавати укрупненими дозами. Скажімо, для ознайомлення учнів з квадратним дециметром насамперед формуємо наочний образ ново одиниці: пропонуємо вирізати з картону чи цупкого паперу модель квадрата зі стороною 10 см, або дм; скласти кілька фігур з таких моделей, обчислити їх площу. Виконуючи вправи, діти швидше запам'ятають, що 1 кв.дм - площа квадрата зі стороню і дм.

Для ознайомлення учнів з палеткою як інструментом для вимірювання площі фігур, можна скористатися прийомом аналогії (масштабна лінійка призначена для вимірювання довжини відрізка, палетка - для вимірювання площі фігур). Вчитель повідомляє учням, що раніше вони знаходили площу фігури тільки прямокутної форми і робили це за правилом. Тепер потрібно навчитись з допомогою особливого пристрою знаходити площу фігур, які мають форму круга, будь-якого многокутника або фігури будь-якої форми. На фігуру накладають палетку - прозору плівку або пластинку, поділену на квадрати - лічать, скільки квадратів цієї палетки накладається на дану фігуру. На дошці вчитель креслить довільну криволінійну фігуру, накладає на неї палетку, показує спосіб підрахунку повних і неповних квадратів. (Палетка вчителя поділена на квадратні дециметри). Використовуючи зображення геометричних фігур, учні за допомогою палетки визначають їх площу.

Як засвідчують спостереження педагогів-дослідників, інтелектуальний рівень дітей за останнє десятиріччя значно підвищився. Це потребує більш високого рівня навчання математики. Класоводи стають перед необхідністю відходити від традиційної методики, шукати нових форм викладання матеріалу. Історичні задачі, практичні роботи, дидактичні ігри значно пожвавлюють “сухий” предмет. Тоді не буде в учнів “легких” і “важких” навчальних дисциплін.