Презентація на тему:
Піраміди

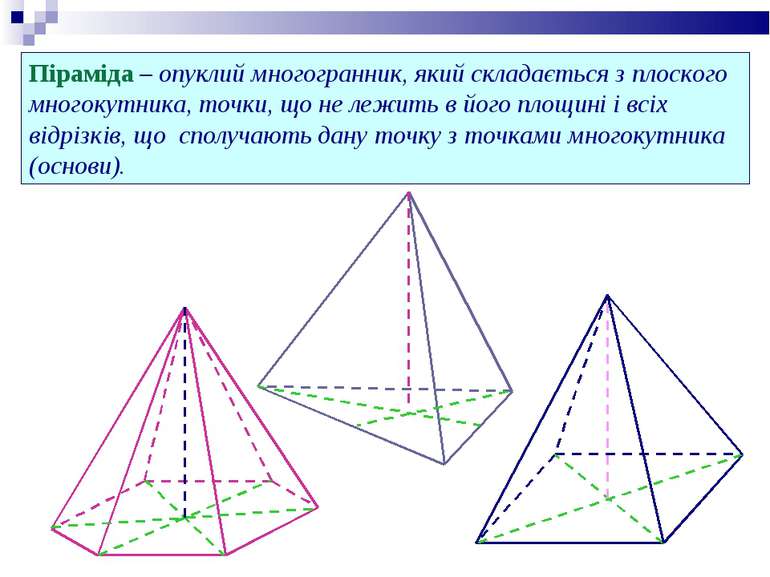
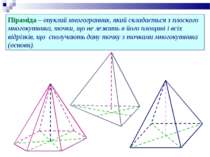
Піраміда – опуклий многогранник, який складається з плоского многокутника, точки, що не лежить в його площині і всіх відрізків, що сполучають дану точку з точками многокутника (основи).

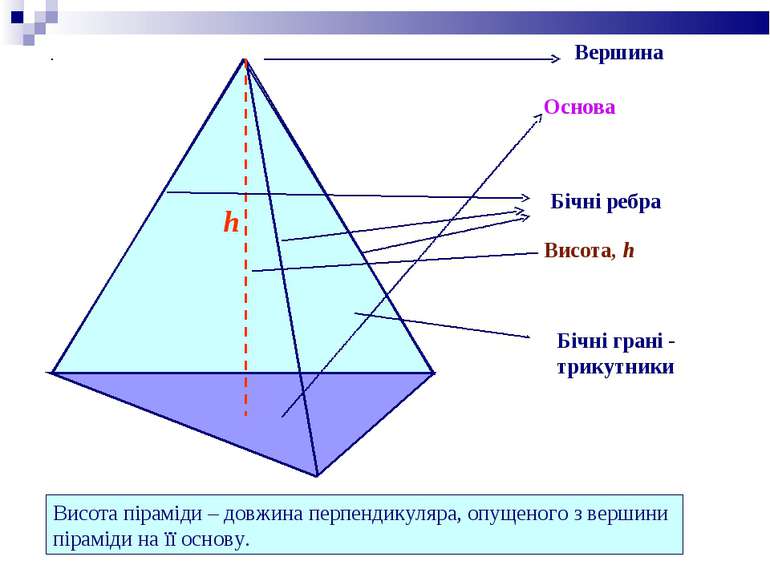
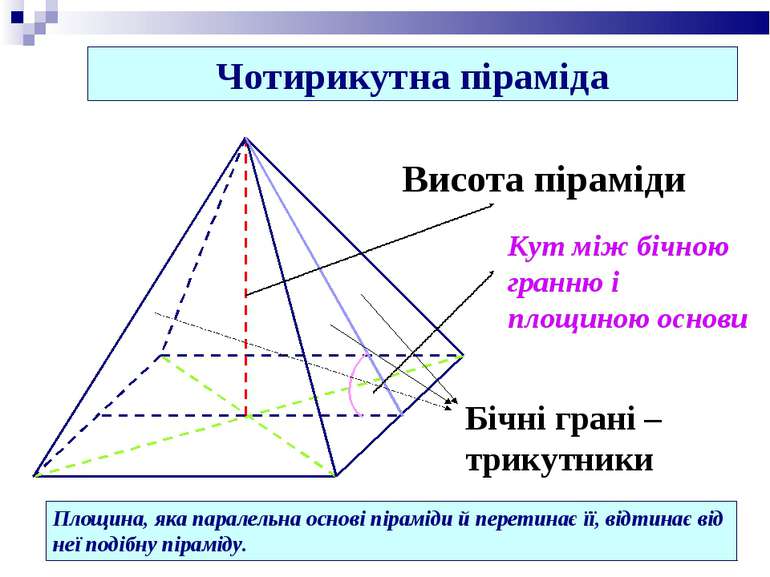
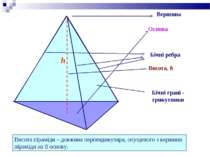
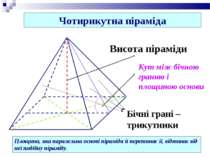
Вершина Основа Бічні ребра Бічні грані - трикутники Висота піраміди – довжина перпендикуляра, опущеного з вершини піраміди на її основу. h Висота, h

Трикутна піраміда O

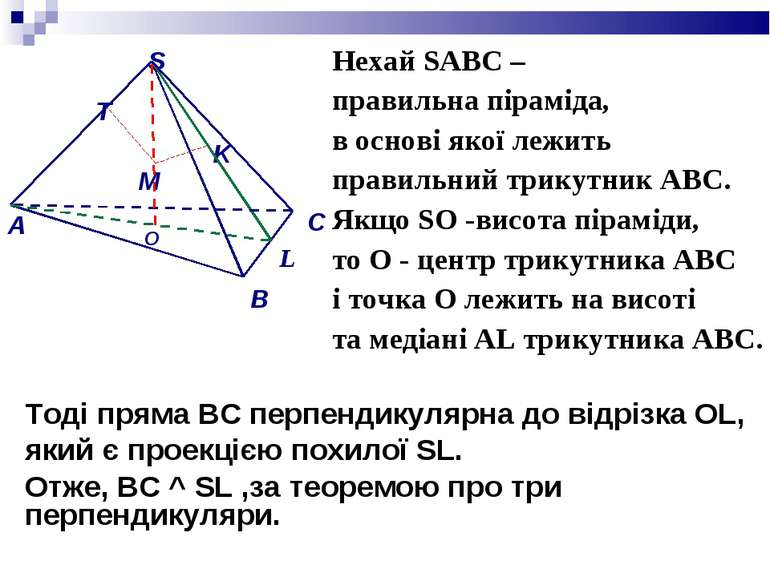
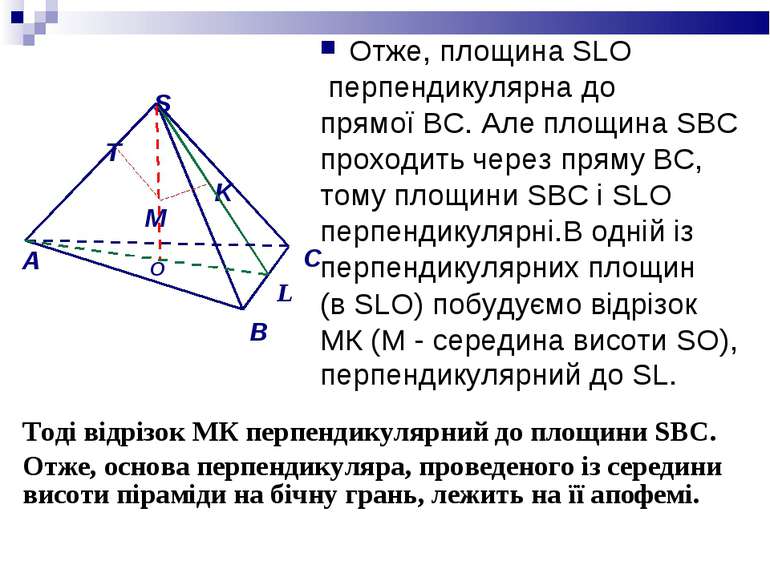
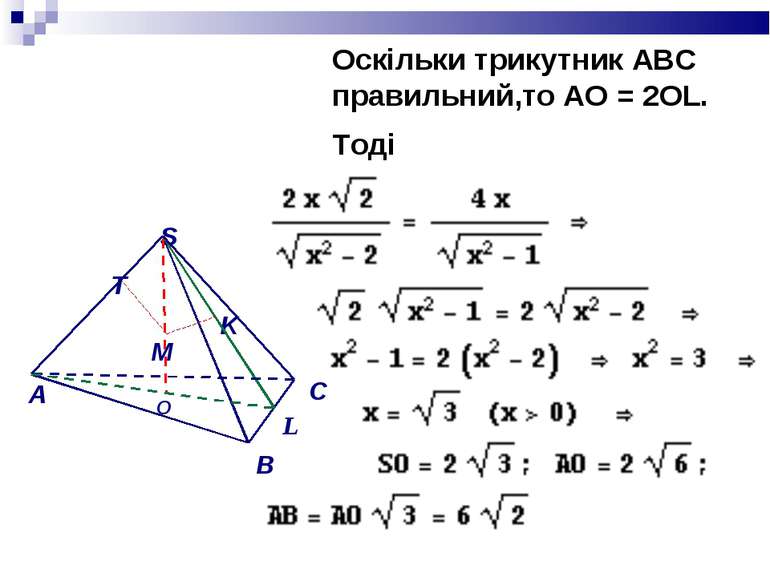
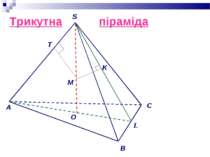
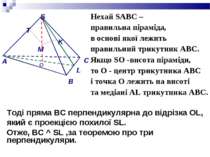
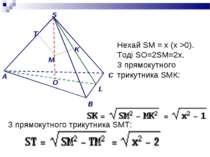
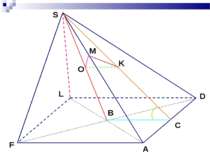
Нехай SАВС – правильна піраміда, в основі якої лежить правильний трикутник АВС. Якщо SО -висота піраміди, то О - центр трикутника АВС і точка О лежить на висоті та медіані АL трикутника АВС. Тоді пряма ВС перпендикулярна до відрізка OL, який є проекцією похилої SL. Отже, ВС ^ SL ,за теоремою про три перпендикуляри. O

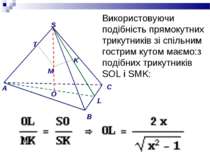
Отже, площина SLO перпендикулярна до прямої ВС. Але площина SВС проходить через пряму ВС, тому площини SBC і SLO перпендикулярні.В одній із перпендикулярних площин (в SLO) побудуємо відрізок МК (М - середина висоти SO), перпендикулярний до SL.  Тоді відрізок МК перпендикулярний до площини SBC. Отже, основа перпендикуляра, проведеного із середини висоти піраміди на бічну грань, лежить на її апофемі. O

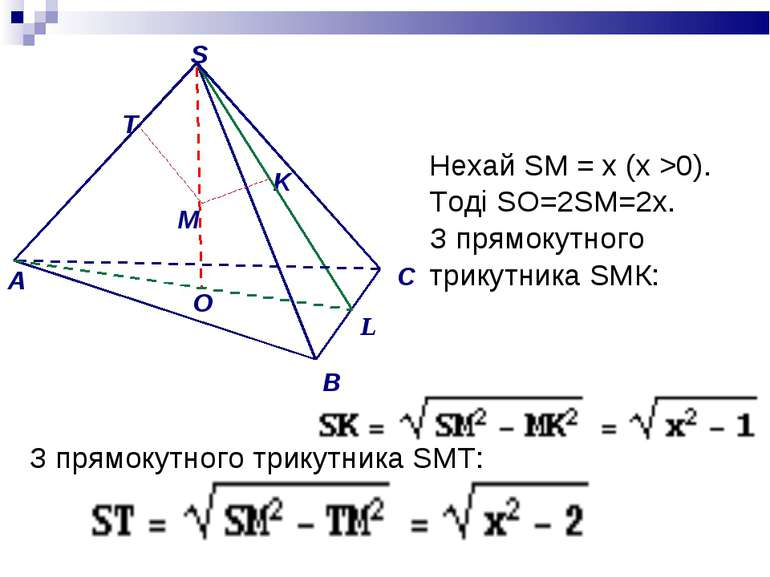
Нехай SM = х (x >0). Тоді SO=2SM=2x. З прямокутного трикутника SМК: З прямокутного трикутника SМТ: O

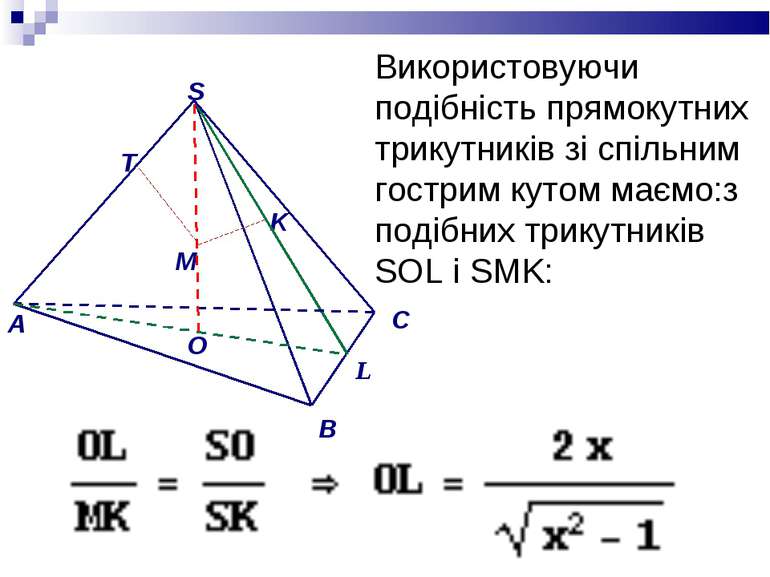
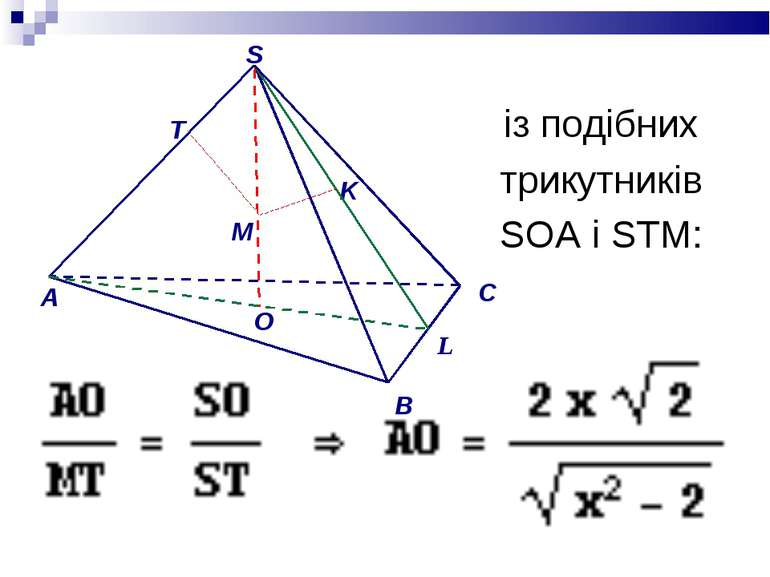
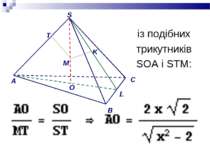
Використовуючи подібність прямокутних трикутників зі спільним гострим кутом маємо:з подібних трикутників SOL i SMK: O

із подібних трикутників SОА і SТМ: O

Оскільки трикутник АВС правильний,то АО = 2ОL. Тоді O

Знайдемо площу основи піраміди = √ 3 O

Чотирикутна піраміда Площина, яка паралельна основі піраміди й перетинає її, відтинає від неї подібну піраміду. Висота піраміди Кут між бічною гранню і площиною основи Бічні грані – трикутники

F S A D L B C O M K

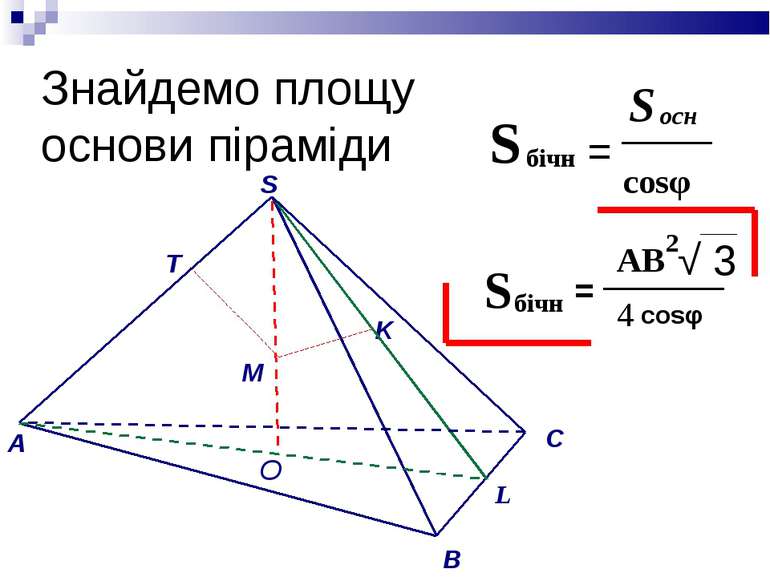
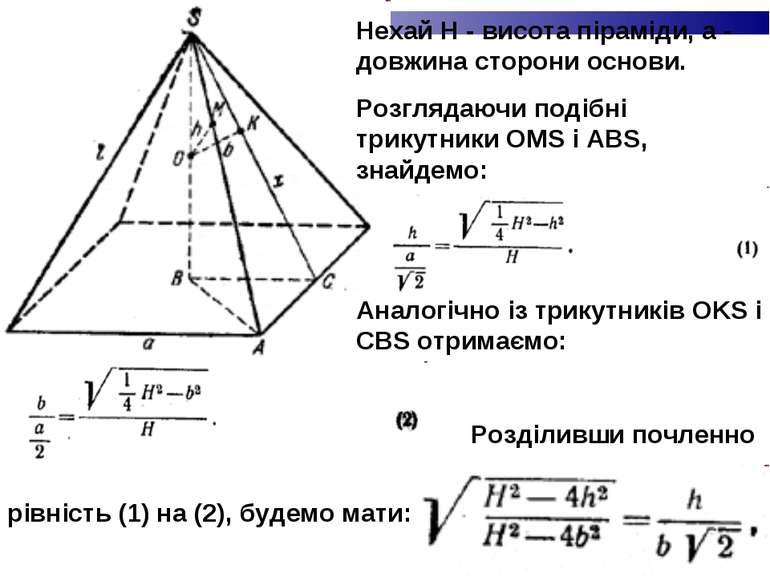
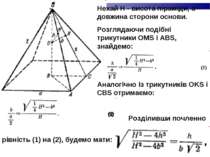
Нехай Н - висота піраміди, а - довжина сторони основи. Розглядаючи подібні трикутники OMS і ABS, знайдемо: Аналогічно із трикутників OKS і CBS отримаємо: Розділивши почленно рівність (1) на (2), будемо мати:

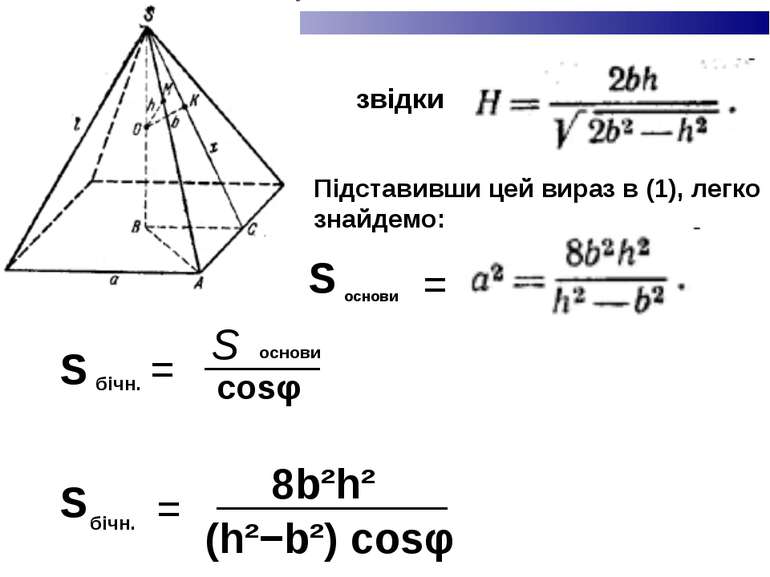
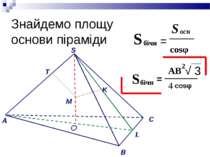
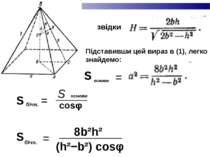
звідки Підставивши цей вираз в (1), легко знайдемо: S основи = S бічн. = ——— S основи cosφ S бічн. = —————— 8b²h² (h²−b²) cosφ

Шестикутна піраміда

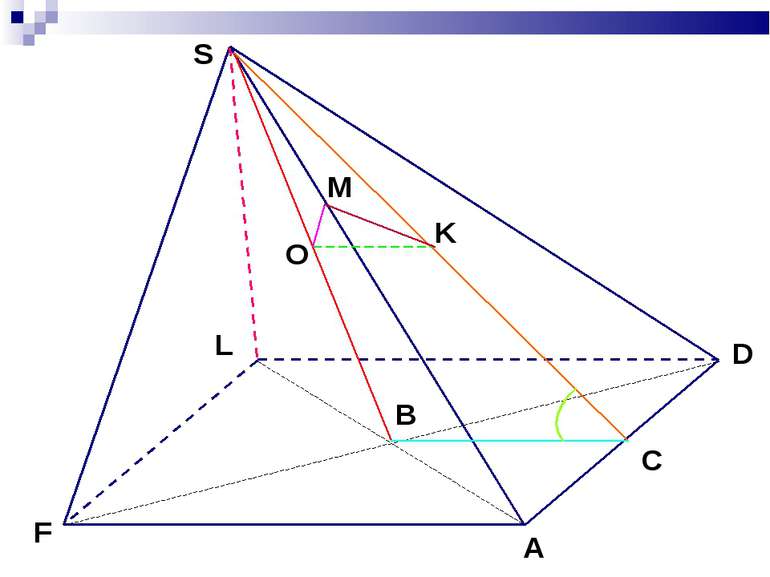
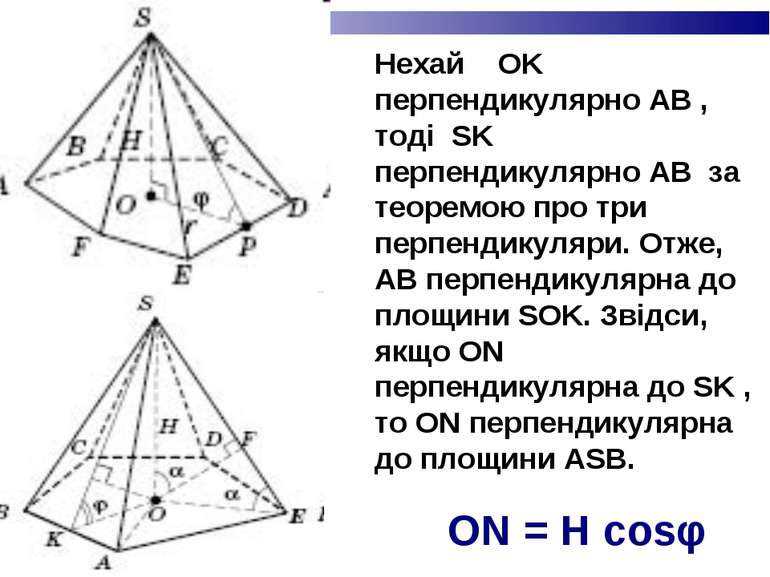
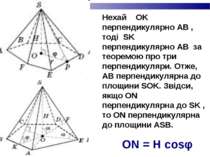
Нехай OK перпендикулярно AB , тоді SK перпендикулярно AB за теоремою про три перпендикуляри. Отже, AB перпендикулярна до площини SOK. Звідси, якщо ON перпендикулярна до SK , то ON перпендикулярна до площини ASB. ON = H cosφ

Дякуємо за увагу! Проект виконали учениці 11-А класу Орлик Юлія та Мельник Анна