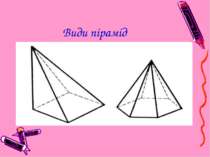
Презентація на тему:
Піраміди

Піраміда. Правильна піраміда. Переріз піраміди

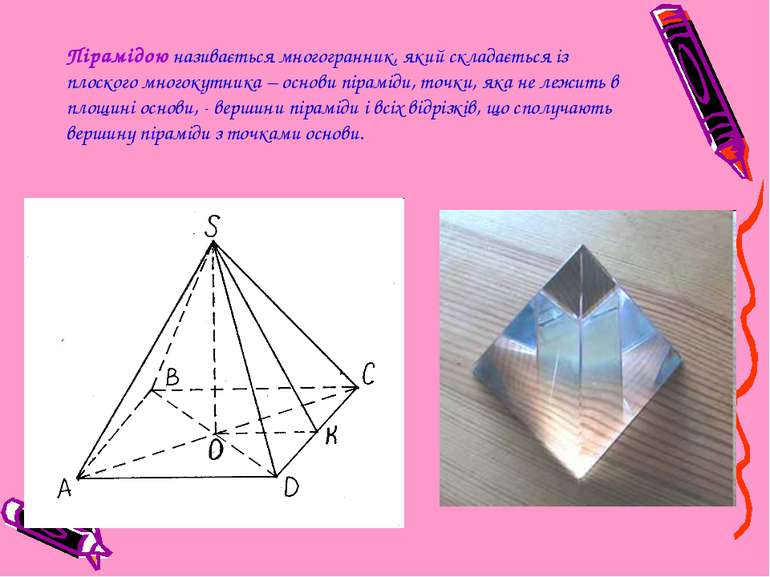
Пірамідою називається многогранник, який складається із плоского многокутника – основи піраміди, точки, яка не лежить в площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи.

Види пірамід

Елементи піраміди ABCD – основа піраміди S – вершина піраміди AB, BC, CD, DA - ребра основи SA, SB, SC, SD - бічні ребра піраміди SO - висота піраміди. Висота піраміди –перпендикуляр, опущений з вершини піраміди на площину основи. Трикутники ASB, BSC, CSD, DSA - бічні грані піраміди

Тетраедр

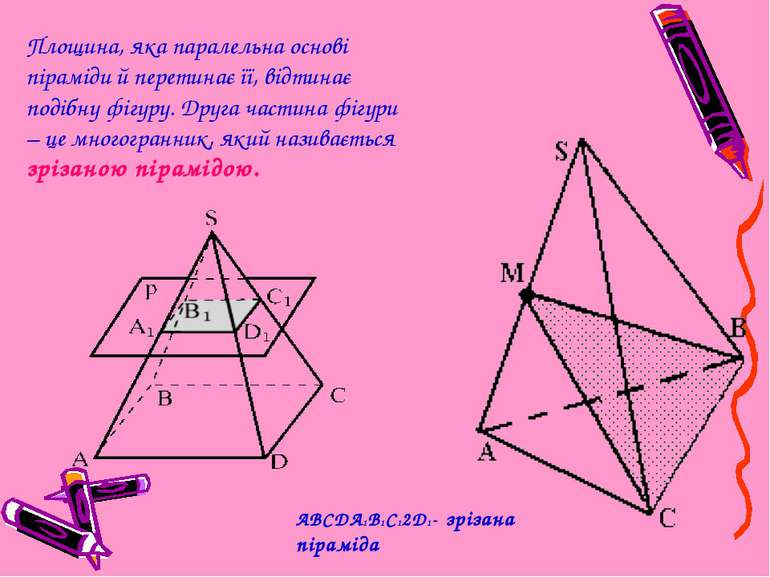
Перерізи піраміди Площина, яка паралельна основі піраміди й перетинає її, відтинає подібну фігуру. Друга частина фігури – це многогранник, який називається зрізаною пірамідою. ABCDA1B1C12D1- зрізана піраміда зрізана чотирикутна піраміда

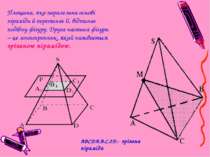
Правильна піраміда Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника Віссю правильної піраміди називається пряма, яка містить її висоту У правильній піраміді всі бічні ребра рівні, бічні грані – рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему. Бічною поверхнею піраміди називається сума площ її бічних граней.

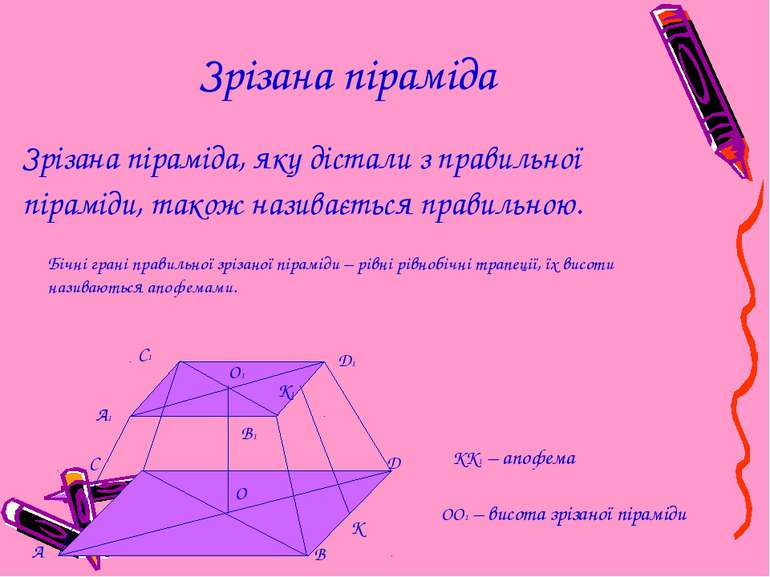
Зрізана піраміда Зрізана піраміда, яку дістали з правильної піраміди, також називається правильною. Бічні грані правильної зрізаної піраміди – рівні рівнобічні трапеції, їх висоти називаються апофемами. A B C D A1 B1 D1 C1 K1 K O O1 OO1 – висота зрізаної піраміди КК1 – апофема

Об’єм піраміди Хеопса V = ⅓ Sоснови · H Параметри піраміди: Висота (Н) – 137 м Основа – квадрат, а тому Sоснови = а² Сторона піраміди – 233 м Обчислюємо об’єм піраміди: V = ⅓ · 233² ·137 = ⅓ · 7437593 ≈ ≈ 2500000 м³ = 2,5 км³ Отже, об’єм піраміди Хеопса приблизно дорівнює 2,5 км³

Нехай РOABC - піраміда; ОАВС – квадрат; АВ=20 дм; РО ḻ (АВС); РО=21дм. Sбіч=SРОА+SРОС+SРВС+SРАВ. ΔРОА=ΔРОС. ΔРСВ=ΔРАВ. Sбіч=2SРОА+2SРАВ. SРОА=½ОА·ОР=½·20·21=210(дм3). Із ΔРОА: РА2=РО2+АО2=212+202=441+400=841 РА=29 дм. ΔРАВ – прямокутний, тоді SАВС=½РА·АВ=½·29·20=290 (дм2). Sбіч=2·210+2·290=2·500=1000(дм2)=10(м2) Відповідь: 10 м2. Задача. Основа піраміди – квадрат, її висота проходить через одну з вершин основи. Знайдіть бічну поверхню піраміди, Якщо сторона основи дорівнює 20 дм, а висота 21 дм. P O А В С