Презентація на тему:
Піраміда. Правильна піраміда. Переріз піраміди

Геометрія 11клас гуманітарний профіль Піраміда. Правильна піраміда. Переріз піраміди

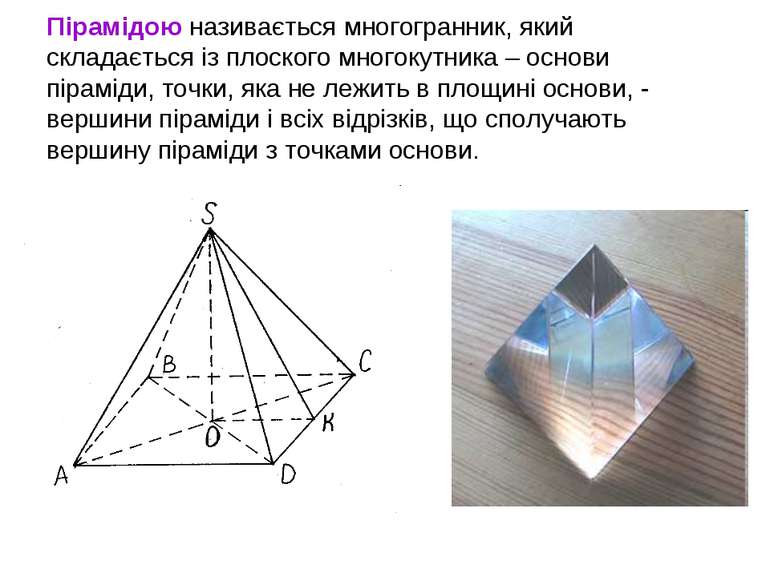
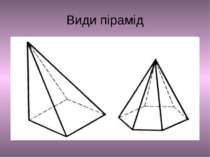
Пірамідою називається многогранник, який складається із плоского многокутника – основи піраміди, точки, яка не лежить в площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи.

Види пірамід

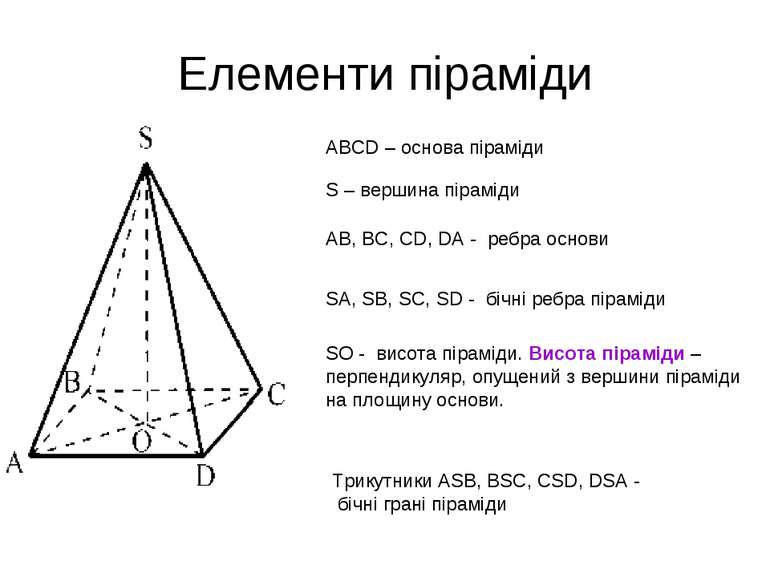
Елементи піраміди ABCD – основа піраміди S – вершина піраміди AB, BC, CD, DA - ребра основи SA, SB, SC, SD - бічні ребра піраміди SO - висота піраміди. Висота піраміди –перпендикуляр, опущений з вершини піраміди на площину основи. Трикутники ASB, BSC, CSD, DSA - бічні грані піраміди

Тетраедр

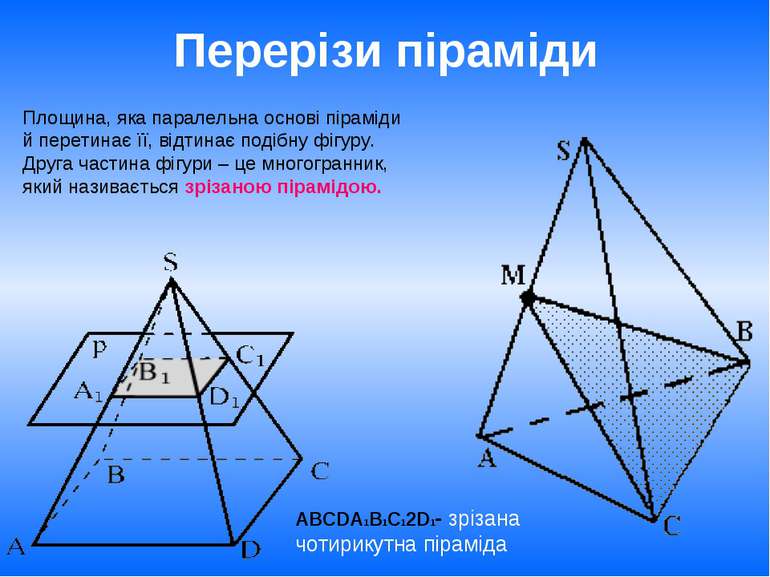
Перерізи піраміди Площина, яка паралельна основі піраміди й перетинає її, відтинає подібну фігуру. Друга частина фігури – це многогранник, який називається зрізаною пірамідою. ABCDA1B1C12D1- зрізана чотирикутна піраміда

Правильна піраміда Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника Віссю правильної піраміди називається пряма, яка містить її висоту У правильній піраміді всі бічні ребра рівні, бічні грані – рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему. Бічною поверхнею піраміди називається сума площ її бічних граней.

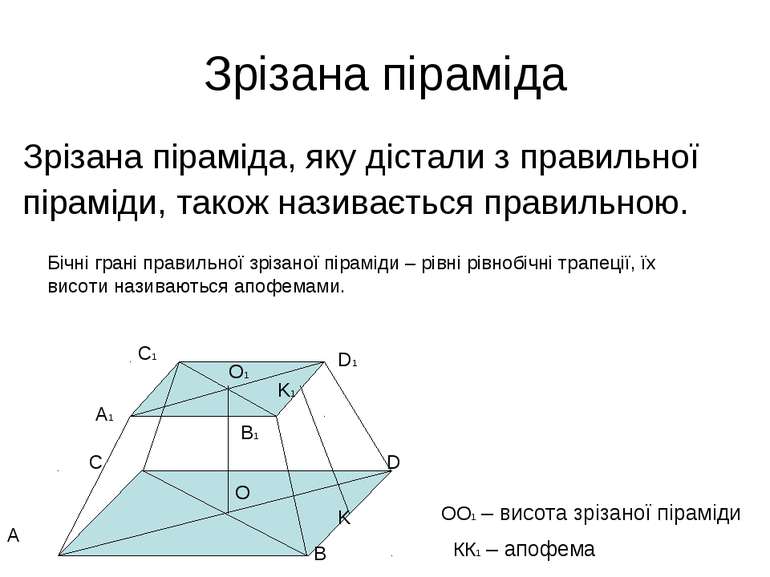
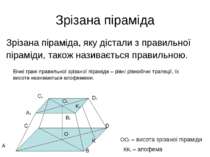
Зрізана піраміда Зрізана піраміда, яку дістали з правильної піраміди, також називається правильною. Бічні грані правильної зрізаної піраміди – рівні рівнобічні трапеції, їх висоти називаються апофемами. A B C D A1 B1 D1 C1 K1 K O O1 OO1 – висота зрізаної піраміди КК1 – апофема

Тренувальні вправи Розв'язати вправи, вказати правильну відповідь

Вказати лінійний кут двогранного кута з ребром АВ, якщо А

В чотирикутній піраміді всі ребра однакові і рівні . Знайти об'єм піраміди Г

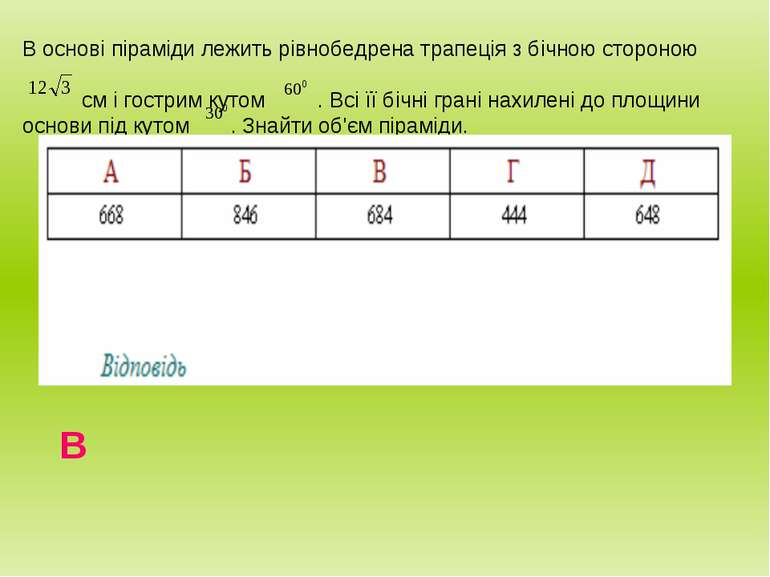
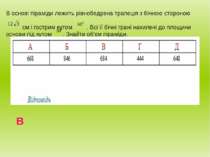
В основі піраміди лежить рівнобедрена трапеція з бічною стороною см і гострим кутом . Всі її бічні грані нахилені до площини основи під кутом . Знайти об'єм піраміди. В

Знайти апофему правильної чотирикутної піраміди, якщо площина основи і бічна поверхня цієї піраміди рівні відповідно і В