Презентація на тему:
"Правильна піраміда"

Правильна піраміда

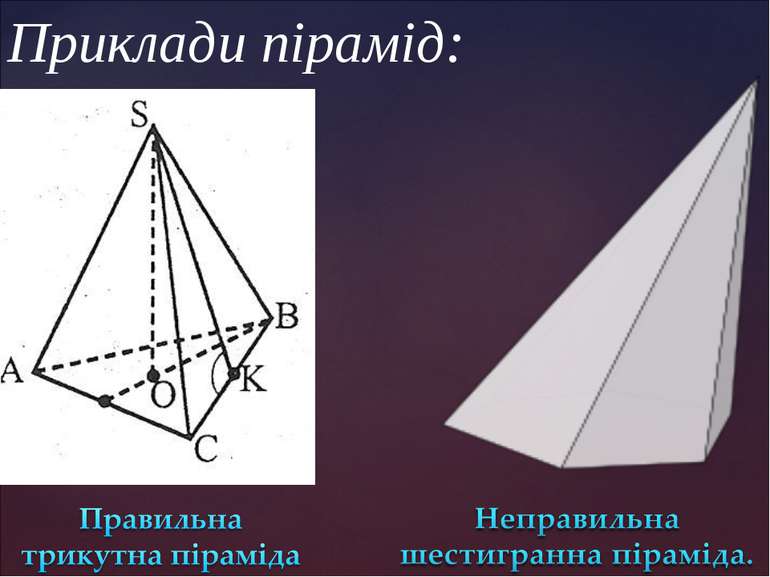
ПІРАМІДОЮ називається многогранник, одна грань якого – довільний многокутник, а інші грані – трикутники, що мають спільну вершину

Приклади пірамід:

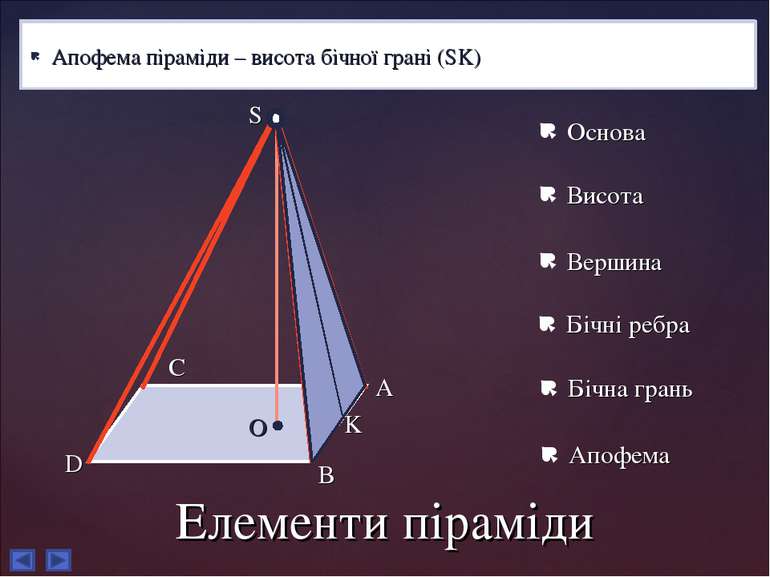
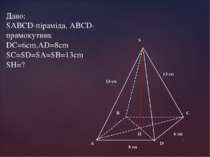
Елементи піраміди Основа піраміди – довільний многокутник, над площиною якого розміщено вершину піраміди (ABCD) Висота піраміди – перпендикуляр, опущений з вершини піраміди на основу (SO) Вершина піраміди – точка, розташована на висоті піраміди, яка проектується на основу цієї піраміди (S) Бічні ребра – Відрізки, що сполучають вершину піраміди з вершинами основи (SA, SB, SC, SD) Бічні грані – трикутники, що мають спільну вершину та утворюють бічну поверхню піраміди (ASB, BSC, CSD, DSA) Апофема піраміди – висота бічної грані (SK) Основа Висота Вершина Бічні ребра Бічна грань Апофема S O A B C D K

Формули площі піраміди

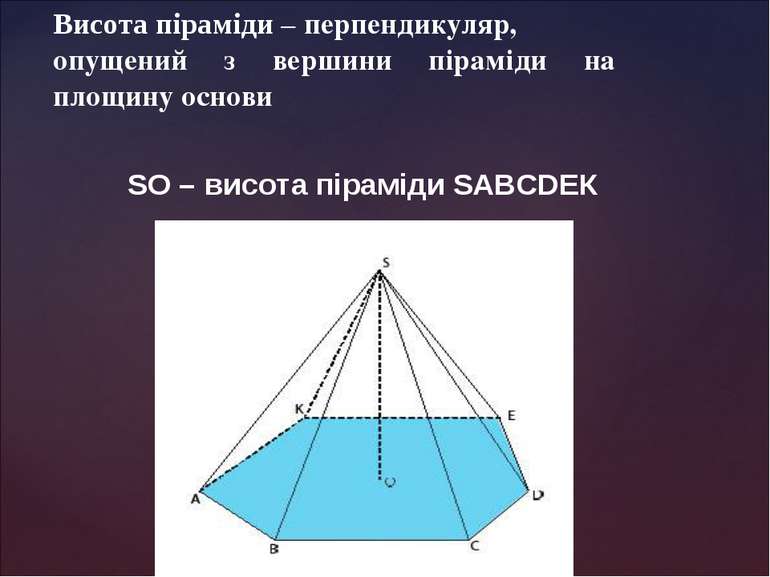
Висота піраміди – перпендикуляр, опущений з вершини піраміди на площину основи SO – висота піраміди SАВСDЕК

Формула площі правильної зрізаної піраміди

Тетраедр

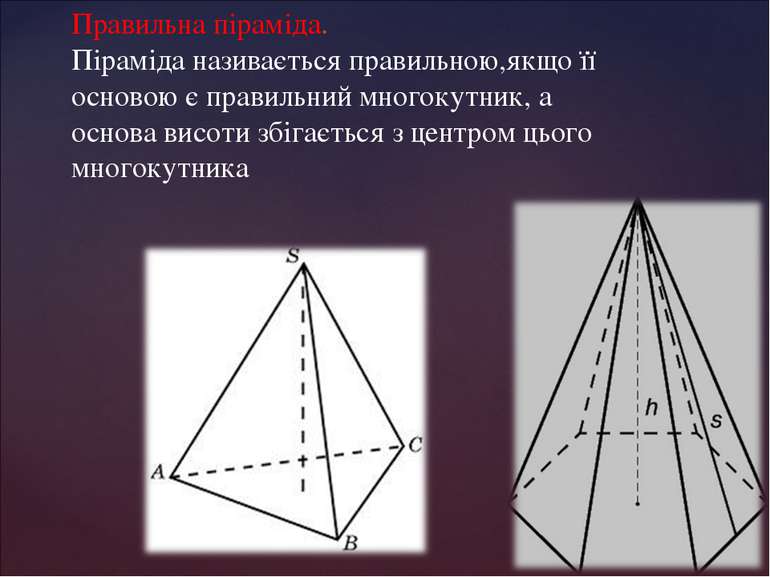
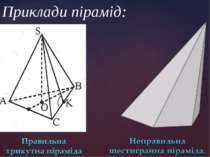
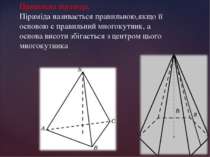
Правильна піраміда. Піраміда називається правильною,якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника

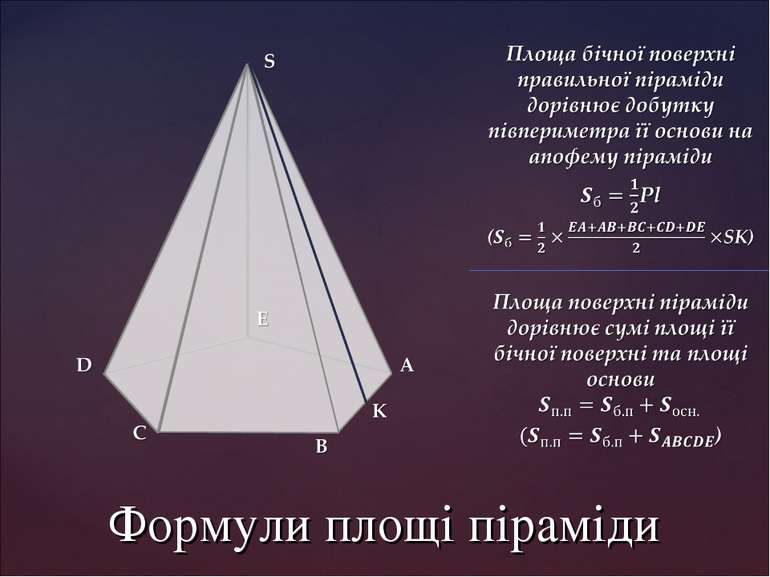
Віссю правильної піраміди називається пряма, яка містить її висоту. У правильній піраміді всі бічні ребра рівні, бічні грані – рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.

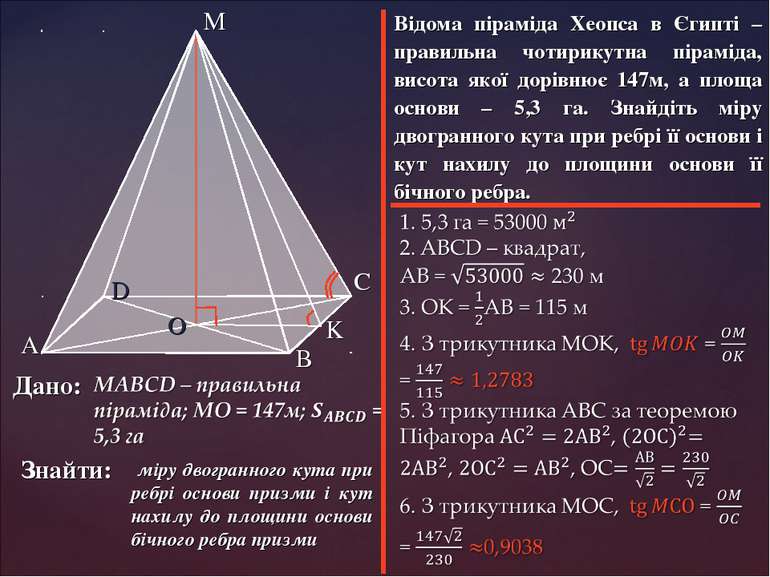
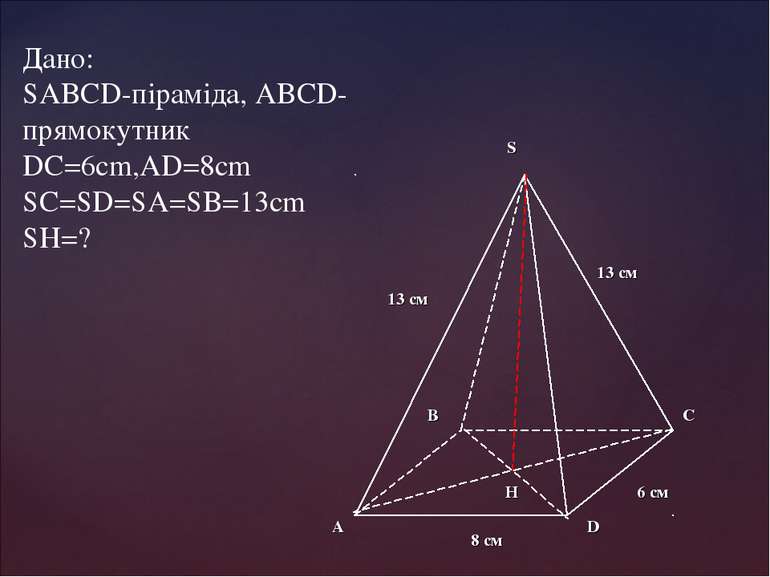
Відома піраміда Хеопса в Єгипті – правильна чотирикутна піраміда, висота якої дорівнює 147м, а площа основи – 5,3 га. Знайдіть міру двогранного кута при ребрі її основи і кут нахилу до площини основи її бічного ребра. Дано: Знайти: міру двогранного кута при ребрі основи призми і кут нахилу до площини основи бічного ребра призми K

Дано: SABCD-піраміда, ABCD-прямокутник DC=6cm,AD=8cm SC=SD=SA=SB=13cm SH=?

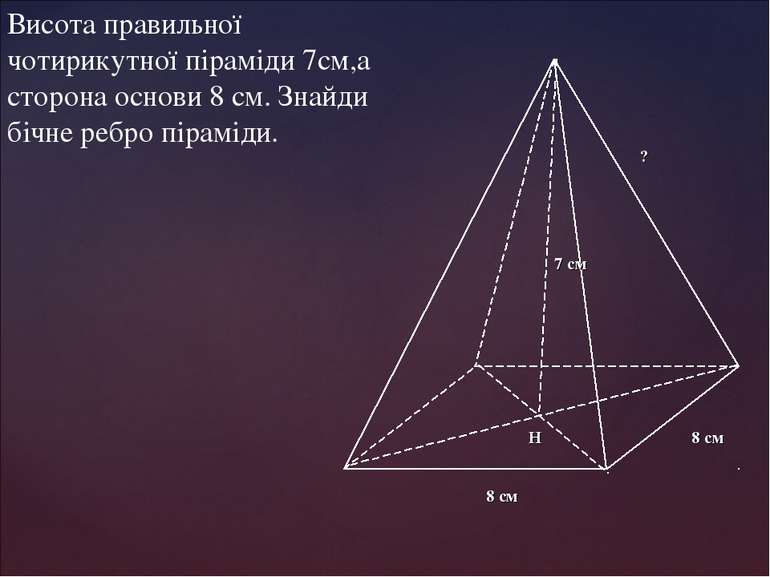
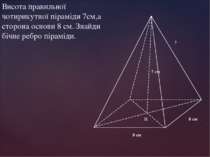
Висота правильної чотирикутної піраміди 7см,а сторона основи 8 см. Знайди бічне ребро піраміди.

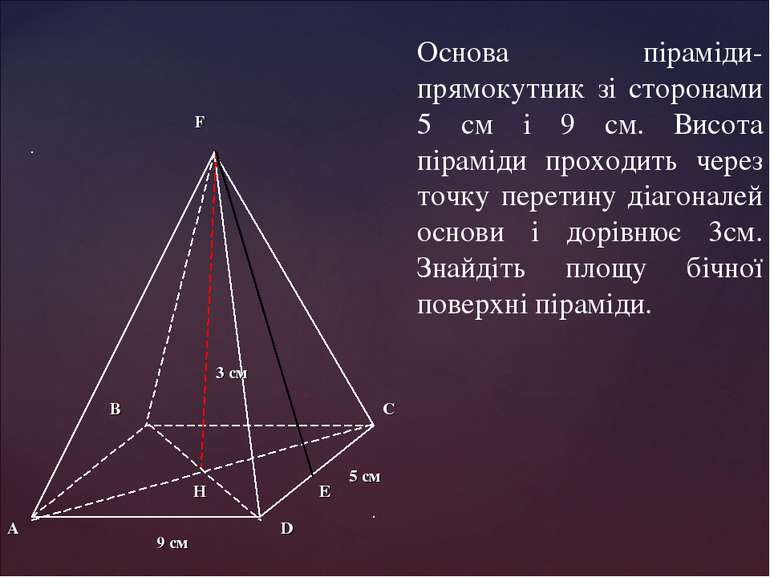
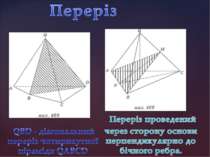
Основа піраміди-прямокутник зі сторонами 5 см і 9 см. Висота піраміди проходить через точку перетину діагоналей основи і дорівнює 3см. Знайдіть площу бічної поверхні піраміди.