Презентація на тему:
ПІРАМІДА. ПРАВИЛЬНА ПІРАМІДА

ПІРАМІДА. ПРАВИЛЬНА ПІРАМІДА

Піраміди В житті ми часто зустрічаємось з пірамідами

Ще 2-3 тис. років до н.е. форми пірамід використовували у побудовах гробниць для фараонів (Хеопса, Хефрена, Мікерина). З давнини піраміди входять в число семи Чудес світу . Найбільша гробниця – Хеопса - була побудована в 27 столітті до н.е. архітектором Хеміуном і спочатку досягала висоти 147 м.

Піраміда Місяця знаходиться в Мексиці. Час спорудження – кінець 1 тис до н.е. - початок н.е. Висота 42 м.

Піраміда Сонця – п'ятиярусна піраміда, знаходиться в Мексиці. Час спорудження – кінець 1 тис до н.е. - початок н.е. Висота 64,5 м.

В 1776 р. Конгресом США прийнято ескіз державної печатки зі зрізаною пірамідою. Якщо подивитися на американську купюру в $1, то на її звороті й нині можна побачити зрізану піраміду, а над нею - трикутник із оком посередині.

Дизайнери-архітектори використовують пірамідальні форми при побудові будинків, ліхтарів на вулиці, дахів на каплицях, церков.

Пірамідальні форми також використовують при виготовленні упаковки для продуктів в харчовій промисловості Ми купуємо пакетики чаю у вигляді пірамід

Упаковка томатної пасти теж для зручності має форму піраміди.

піраміди

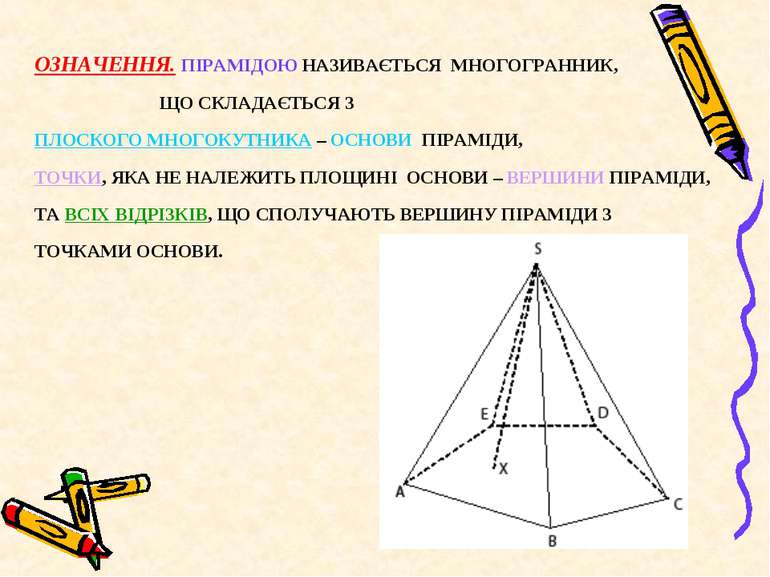
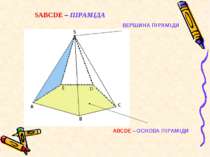
ОЗНАЧЕННЯ. ПІРАМІДОЮ НАЗИВАЄТЬСЯ МНОГОГРАННИК, ЩО СКЛАДАЄТЬСЯ З ПЛОСКОГО МНОГОКУТНИКА – ОСНОВИ ПІРАМІДИ, ТОЧКИ, ЯКА НЕ НАЛЕЖИТЬ ПЛОЩИНІ ОСНОВИ – ВЕРШИНИ ПІРАМІДИ, ТА ВСІХ ВІДРІЗКІВ, ЩО СПОЛУЧАЮТЬ ВЕРШИНУ ПІРАМІДИ З ТОЧКАМИ ОСНОВИ.

SАВСDЕ – ПІРАМІДА АВСDЕ – ОСНОВА ПІРАМІДИ ВЕРШИНА ПІРАМІДИ SАВСDЕ – ПІРАМІДА

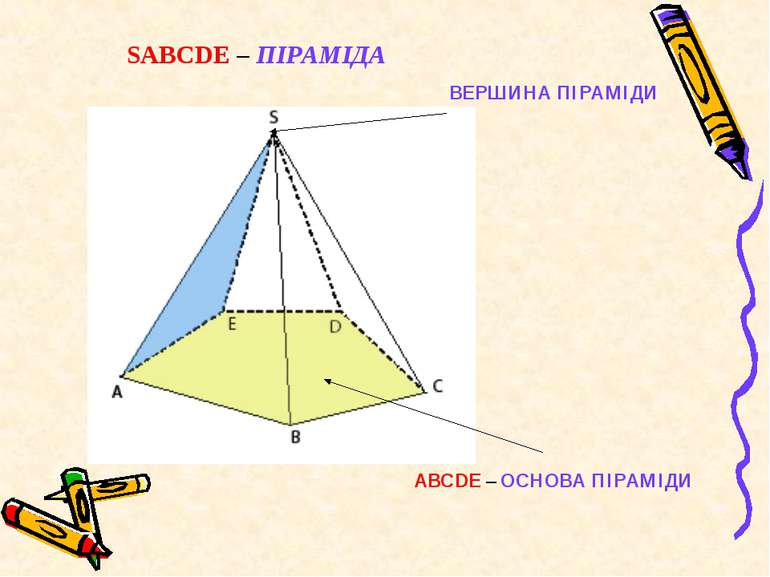
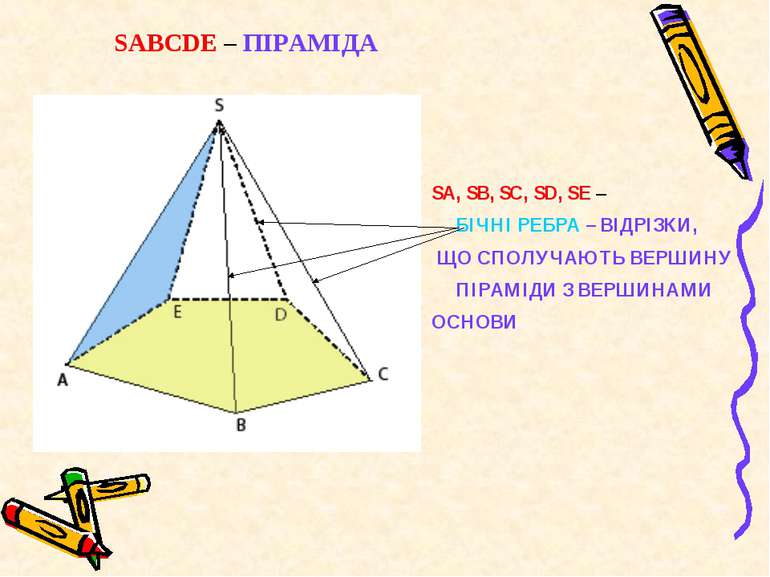
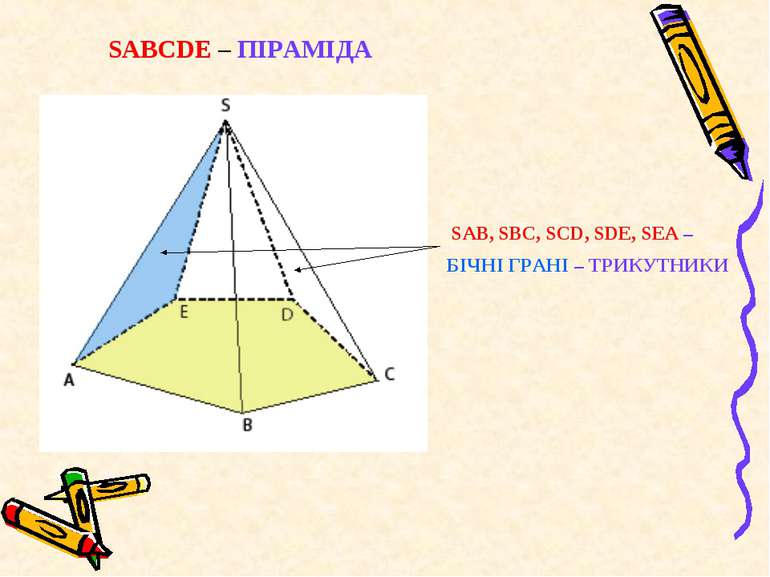
SА, SВ, SС, SD, SЕ – БІЧНІ РЕБРА – ВІДРІЗКИ, ЩО СПОЛУЧАЮТЬ ВЕРШИНУ ПІРАМІДИ З ВЕРШИНАМИ ОСНОВИ SАВСDЕ – ПІРАМІДА

SАВ, SВС, SСD, SDЕ, SЕА – БІЧНІ ГРАНІ – ТРИКУТНИКИ SАВСDЕ – ПІРАМІДА

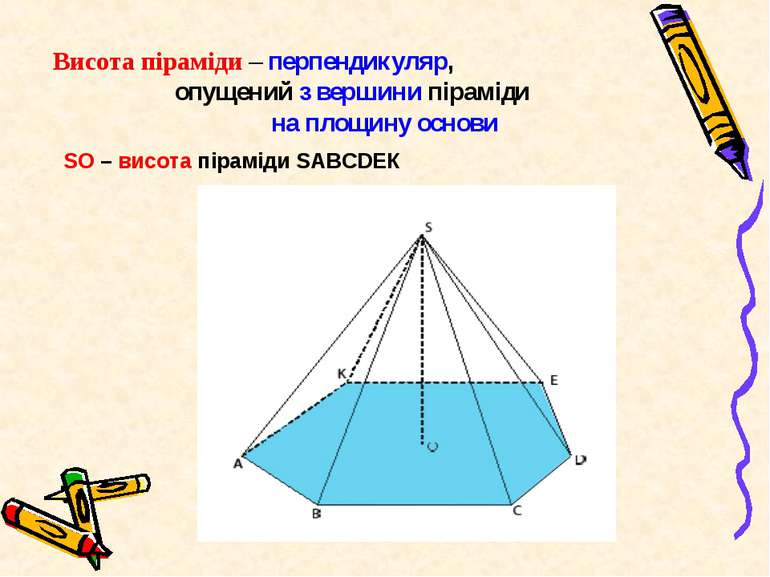
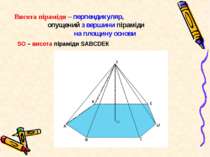
Висота піраміди – перпендикуляр, опущений з вершини піраміди на площину основи SO – висота піраміди SАВСDЕК

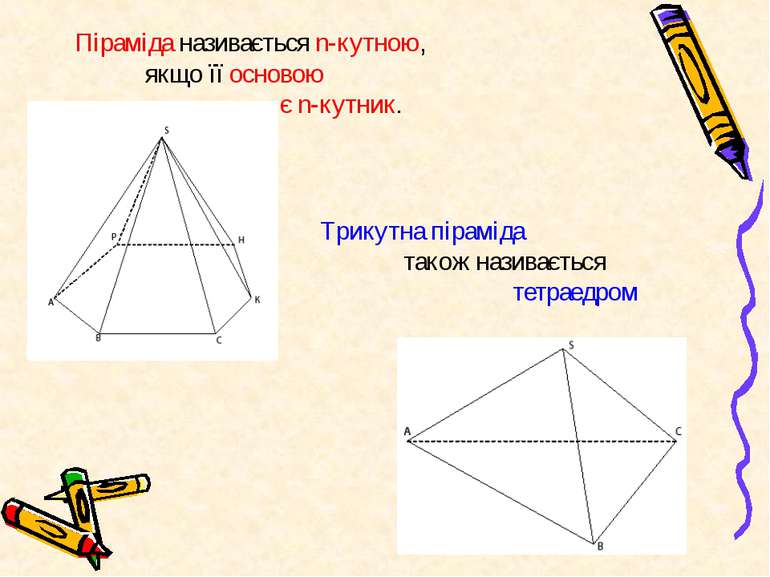
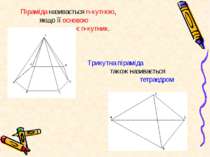
Піраміда називається n-кутною, якщо її основою є n-кутник. Трикутна піраміда також називається тетраедром

ОЗНАЧЕННЯ 1. Піраміда, в основі якої лежить правильний многокутник і всі бічні ребра рівні між собою, називається правильною. ОЗНАЧЕННЯ 2. Піраміда, в основі якої лежить правильний многокутник і основа висоти піраміди збігається з центром цього многокутника, називається правильною.

ДАНО: АВСD – правильний чотирикутник. SO ┴ (АВС), SA=SB=SC=SD ДОВЕСТИ: О – центр АВСD

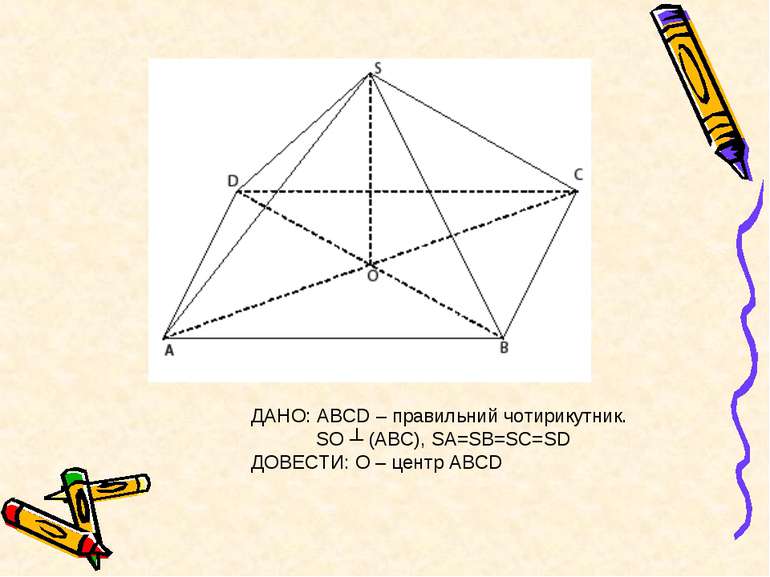
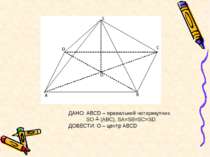
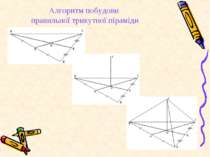
ПЛАН ДОВЕДЕННЯ. 1. Розгляньте ∆SOA, ∆SOB, ∆SOC, ∆SOD. Які вони? Чому? 2. Які елементи спільні в цих трикутників, які рівні? 3. Пригадайте ознаку рівності прямокутних трикутників. Який висновок ви зробили? 4. Що слідує з рівності ∆? 5. Що це означає?

ДОВЕДЕННЯ. Розглянемо ∆SOA, ∆SOB, ∆SOC, ∆SOD. 1. З умови SO ┴ (АВС) SOA= SOB= SOC= SOD= 900, отже ∆-ки прямокутні. 2. SO – спільна (катет), SA=SB=SC=SD(гіпотенуза) за умовою. За ознакою рівності прямокутних ∆-ків маємо: ∆SOA= ∆SOB= ∆SOC= ∆SOD. 3. З рівності ∆-ків слідує рівність їх відповідних елементів. Отже, OA=OB=OC=OD, а це означає, що т.О – центр описаного кола. Що і треба було довести.

Алгоритм побудови правильної трикутної піраміди

БАЖАЮ УСПІХУ!