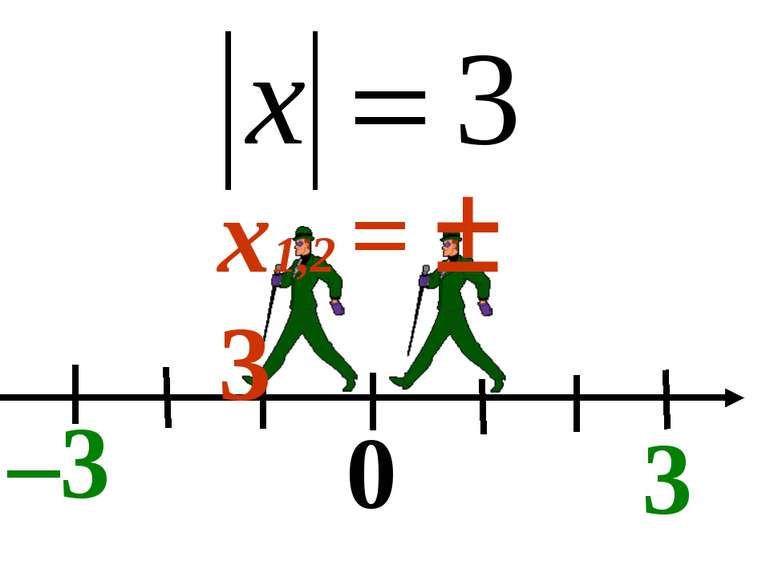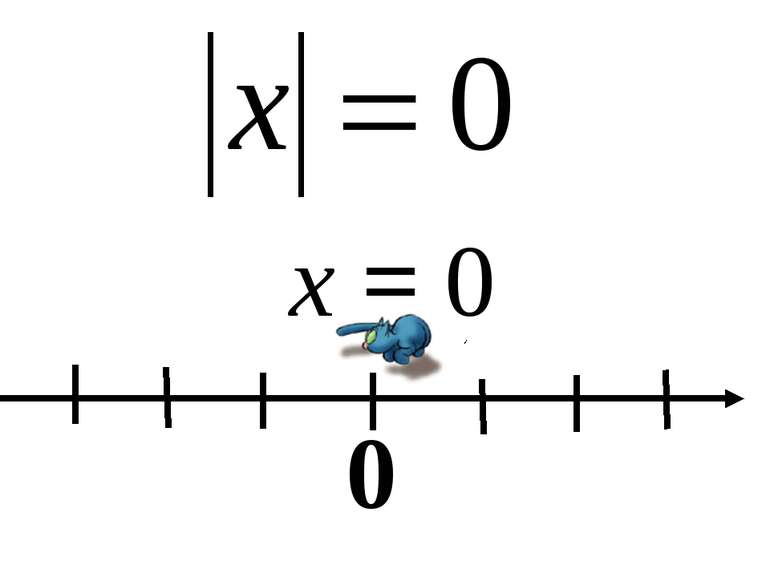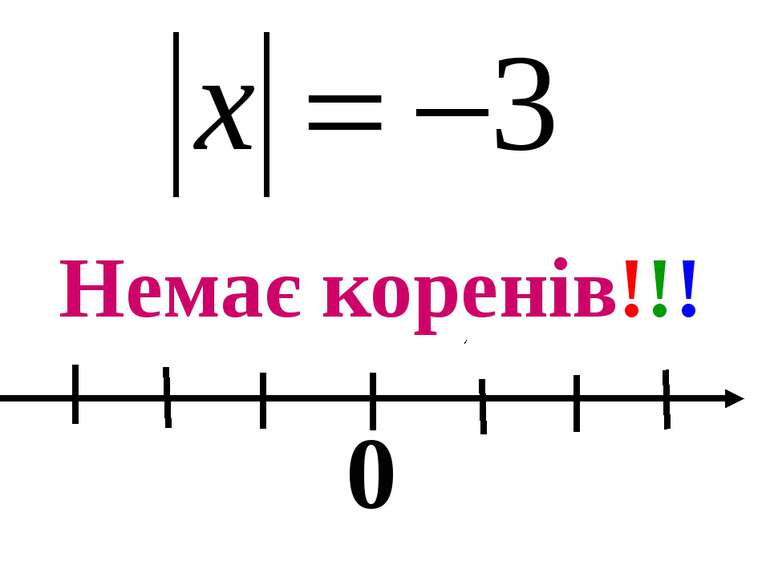Презентація на тему:
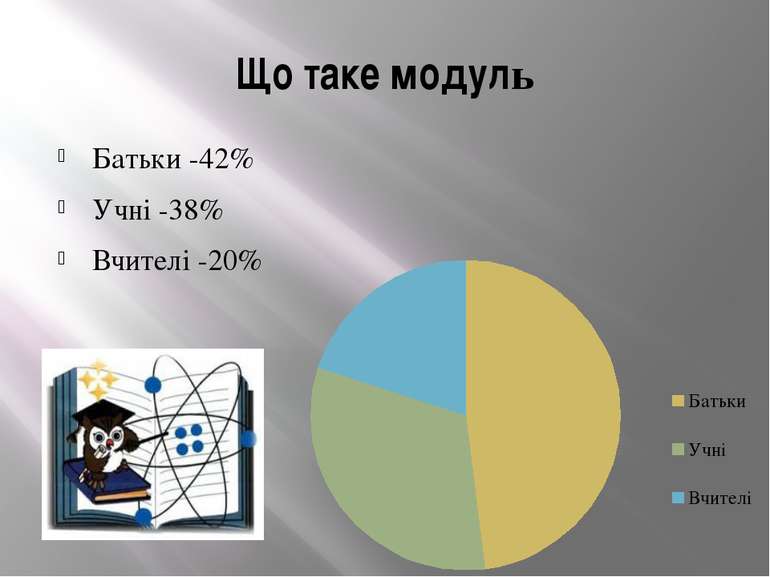
Модуль у світі Від’ємних чисел

Модуль у світі Від’ємних чисел Учні 6-А класу вчитель математики Маршалко Н. В. Перегінської ЗОШ №2 I-III ступенів

Мета і завдання проекту

Соціологи Пальчинська М. Горбоконь Т. Волошин В. Халус А. Тринчук М.

До всіх я поважний, Завжди я додатний, Для додатних і нуля Сил своїх не трачу я, А у чисел від’ємних Я минус забираю. Розрахую відстань Від початку відліку до точки А, Я найвеличніший! Я модуль числа ! 1

Що таке модуль Батьки -42% Учні -38% Вчителі -20%

Як позначається модуль Батьки-50% Учні-37% Вчителі-23%

Знайти модуль числа

В і д є м н і П р о т и л е ж н і Д і а г р а м а К р у г Р а ц і о н а л ь н і Н у л ь

Дроцюк Я. Халус О. Семкович І. Романко О. Христук С. Історики

Ідеї виникнення нових чисел людство виношувало століттями і навіть тисячоліттями. Величезним досягненням людського розуму був винахід цифри 0. Адже віками нікому не спадало на думку, що порожнє місце можна якось позначати. Історія виникнення поняття “модуля” Італійський математик Дж. Кардано у XVI ст. при розв’язуванні рівнянь користувався від’ємними числами, але називав їх фіктивними.В узаконення від’ємних чисел зробив видатний французький вчений Рене Декарт, “виділивши їм житло” на координатній прямій ліаоруч від нуля.

= = = = x x x x

Термін “модуль” увів в математику учень видатного вченого Ньютона – Роджер Котес. А позначення модуля: ׀а׀ було введено в середині XIX століття відомим німецьким математиком – Вейєрштрасом.

Ребус. П = Р я / КАРЛ

М. В. Остроградський М. В. Остроградський народився на Полтавщині 1801 року, вже в дитинстві він завжди ходив із шнурком у кишені, прив'язавши до нього камінець, за допомогою якого вимірював глибину всіх криниць. Остроградський навчався в гімназії, в Харківському університеті на механіко-математичному факультеті. У 1822 році він їде до Парижа, де привертає до себе увагу французьких учених. Його вважали науковим авторитетом у галузі математики і механіки, символом стійкості та енергії. М. В. Остроградський був чудовим учителем, він писав: "Краще вчиться не той, хто старанно за пам'ятовує прочитане, а той, хто набуває вміння використати його".

М О Д У Л Ь 0 1,5 0,8 Вкажіть число, протилежне даному , а у другій таблиці знайдіть букву, яка відповідає цьому числу. 0 0,1 0,8 0 1,5 О Ь М Д Л У

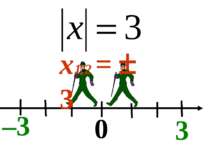
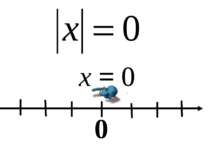
Означення модуля: Модулем додатного числа а є саме число а. Модулем числа 0 є число 0. Модулем від’ємного числа а є протилежне йому число –а. Модуль числа – це число, взяте без знака.

Означення модуля a, якщо a > 0; 0, якщо а = 0; -а, якщо а < 0.

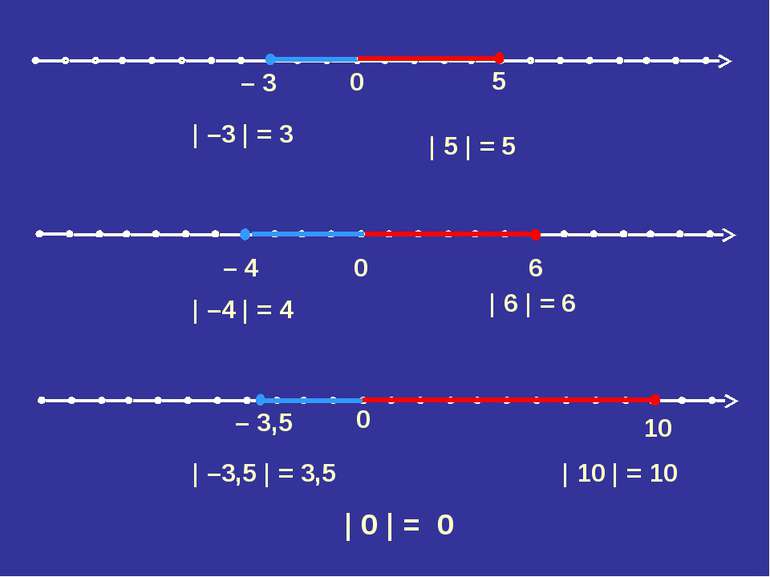
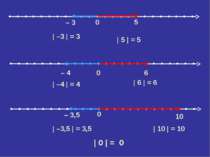
0 – 3,5 10 0 – 4 6 | –3 | = 3 | 5 | = 5 | –4 | = 4 | 6 | = 6 | –3,5 | = 3,5 | 10 | = 10 | 0 | = 0 0 – 3 5

0 – а а | – а | = а | а | = а | – а | = | а | модуль числа не може бути від’ємним; модулі протилежних чисел рівні.

Знайдіть значення виразу: |-8|-|-5| |-10|*|-5| |240|:|-80| |-710|+|-290| = 8 - 5 = 3 = 10 * 5 = 50 = 240 : 80 = 3 = 710 +290 = 1000

15 і 28; 13,7 і 8,6; і ; 12,3 і 12,29; -4 і -1. Порівняймо числа:

-4 і -1 З двох від’ємних чисел меншим буде те число, у якого більший модуль. ׀-4׀ > ׀-1׀

Прикольно! Уявімо, що модуль – це баня, а знак «мінус» - грязь. Виявившись під знаком модуля, від’ємне число «миється» і виходить без знака «мінус» - чистим. В бані можуть «митися» (т.ч. стояти під знаком модуля) як додатні, так і від’ємні числа.

Науковці Глинка А. Семкович Д. Полич Д. Писар Б. Мельникович В.

0 –3 3 x1,2 = 3

0 х = 0

0 Немає коренів!!!

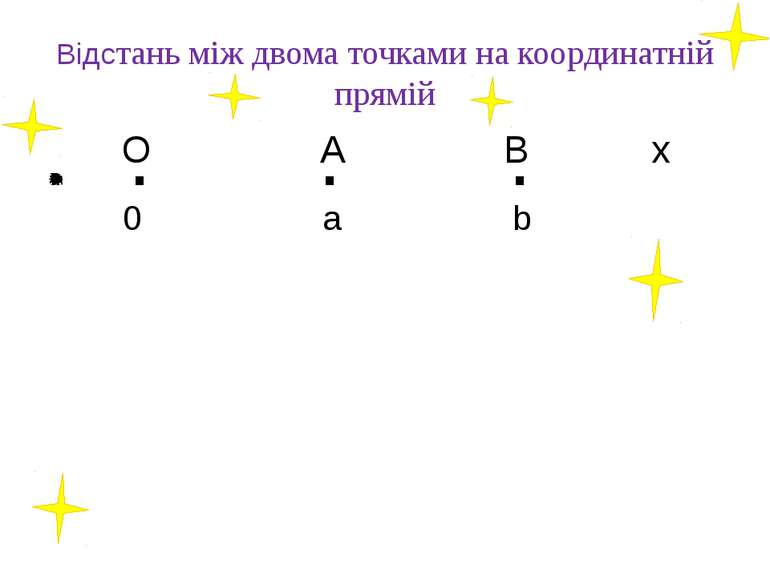
Відстань між двома точками на координатній прямій Дано А(а) і В(b), b>a додатні; АВ = ОВ - ОА = b – a = ׀b׀ – ׀a׀. Якщо А(5,3); В(7,25), то АВ = 7,25 – 5,30 = 1.95 (од. відр.) . . . O A B 0 a b x

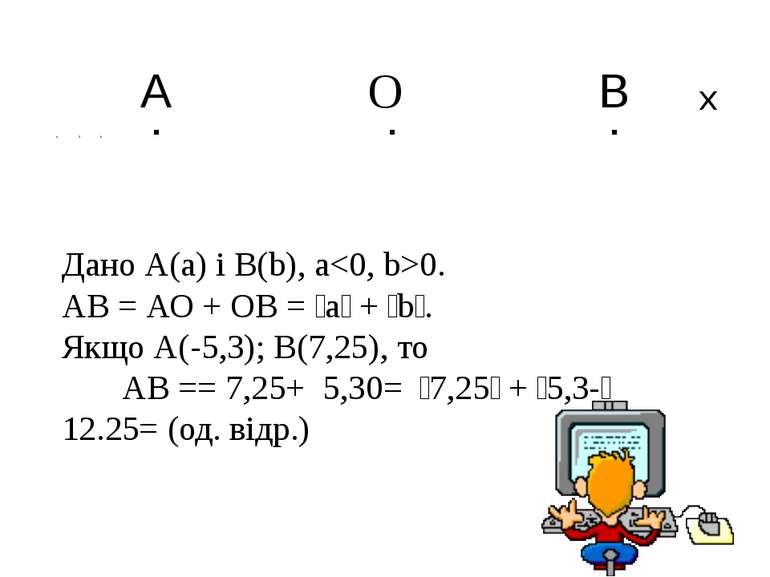
А О B а 0 b . . . х Дано А(а) і В(b), а0. АВ = АО + ОВ = ׀а׀ + ׀b׀. Якщо А(-5,3); В(7,25), то АВ =׀-5,3׀ + ׀7,25׀ = 5,30 + 7,25 = =12.25 (од. відр.)

В A О . . . х b a 0 Дано А(а) і В(b), а

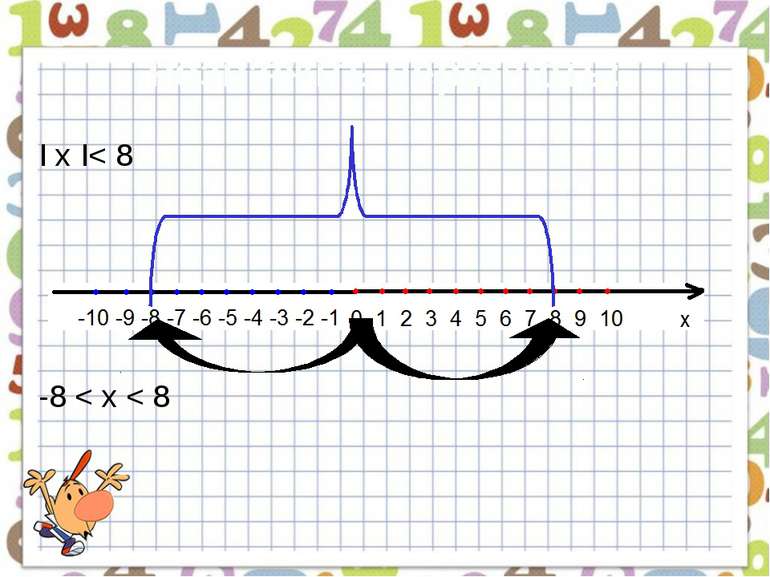
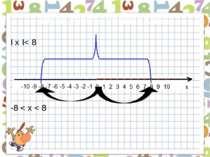
Як розв’язати нерівність ׀х׀< а (а>0)? . . . -а 0 а х // / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / За означенням модуля цю нерівність задовольняють усі числа, відстань від яких до точки О(0) менша за а. Тобто -а < х < а.

Розв’яжіть нерівність: І х І< 8 -8 < х < 8

Висновок Означення і властивості модуля ми використовуємо для: знаходження модуля числа; розв’язування рівнянь ׀х׀ = а; розв’язування нерівностей ׀х׀ < а; знаходження відстані між двома точками на координатній пямій.

1. Обчислити: ׀-71׀ А) -71; Б) 71; В)7; Г) -71 і 71. 2. Знайти значення виразу: ׀ -11׀ - ׀ -9׀. А) 20; Б) -2; В)2; Г)-20. 3.Розв’язати рівняння: ׀х׀ = 6,5. А) +6,5; Б) -6,5; В)- 6,5 і 6,5; Г) коренів немає. 4. Обчислити: -6 + (-6,2). А)-0,2; Б) -12,2; В) 12,2; Г) -17. 5. Знайти значення виразу ׀х + 5׀, якщо х = -1. А) 4; Б) -4; В) 6; Г) -6. 6. Розв’язати рівняння: |х| = -3. А) коренів немає; Б) -3; В) 3; Г) -3 і 3. 7. Розв’язати рівняння: ׀ х – 5׀ = 0. А) -5 і 5; Б) коренів немає; В) 5; Г) -5. 8. Обчислити: ׀ -43׀ +5* ׀4׀. А) 63; Б)81; В) -15; Г) 41. 9. Які числа належать до розв’язків нерівності: |х| > 4? А) -5 і 2; Б) -6 і -7; В) -10 і 4; Г) 7 і 3. 10. Розв’язати рівняння: ׀ х׀ + 2 = 5. А) -7 і 7; Б) -3 і 3; В) коренів немає; Г) 3. 11. Яка з нерівностей є правильною: А) ׀-71׀ ׀100׀; Г) ׀0׀ > ׀ -12,4׀. 12. Знайти відстань між точками: А(-4,1) і В(6,2). А) 10,3; Б) -10,3; В) -2,1; Г) 2,1.

МОЛОДЦІ!