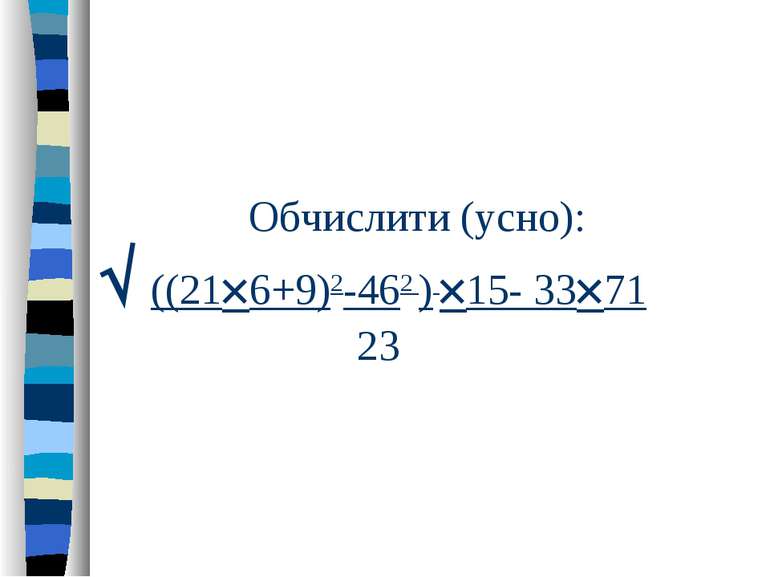Презентація на тему:
Методи усних обчислень

Методи усних обчислень Пєшкова Марина 21 МФІ група

В методиці математики розрізняють усні та письмові прийоми обчислень. Навчитися швидко рахувати не так вже й складно, а гарному фізику та математику просто необхідно В історії математики відомо біля 30 загальних способів множення

Обчислити (усно): ((21 6+9)2-462 ) 15- 33 71 23

Множення

Множення методом Ферроля Для одержання одиниць перемножимо одиниці співмножників, для одержання десятків перемножують десятки одного на одиниці другого співмножника і навпаки,а потым результати додають, для одержання сотень перемножують десятки. (10a + b)(10c + d)=100ac + 10(ad + bc) + bd.

Множення на одноцифрове число Щоб помножити число на одноцифровий множник (наприклад, 27 8), виконують дії, починаючи з множення не одиниць, як при письмовому множенні, а навпаки: множимо спочатку десятки множеного (20 8=160), а потім одиниці (7 8=56) та додаэмо обидва результати (160+56=216).

Отримуємо: ((126+9)2-462 ) 15- 33 71 23 (1352-462 ) 15- 33 71 23 Застосуємо до нашого прикладу: 21 6=126 20 6=120 1 6=6 120+6=126

Множення на двоцифрове число Множення на двоцифрове число намагаються полегшити для усного виконання, приводячи цю дію до більш звичного множення на одноцифрове число. Якщо ж обидва множники двоцифрові, подумки розбивають один з них на десятки та одиниці. Якщо множник або множене легко розкласти подумки на одноцифрові числа (наприклад, 14=2 7), то користуються цим

Отримуємо: (1352-462 ) 15- 2343 23 Застосуємо до нашого прикладу: 33 71= 71 30+71 3=2130+213=2343

Множення “пірамідою” Множимо цифри, що стоять одна під одною, виділяючи по 2 знаки на кожен результат. Множимо навхрест сусідні цифри. Результат пишемо зі зсувом на 1 знак вліво під результатом першого кроку. .“Розсуваємо” крок хреста на одну позицію. Під нього попадають тільки крайні цифри. Записуємо їхный добуток під результатом попередного кроку зі зсувом на 1 знак вліво

Спрощене піднесення числа до степеня і добування з числа кореня n-го степеня

Піднесення до квадрату чисел, що закінчуються на 5 Щоб піднести до квадрату число, що закінчується цифрою 5 (наприклад, 85), множать число десятків (8) на нього ж, плюс одиниця (8*9=72) та дописують 25 (у нашому прикладі виходить 7225). Наступні перетворення показують, що застосування такого прийому є цілком коректним (10x+5)2=100x2+100x+25=100x(x+1)+25.

Отримуємо: (18225-462 ) 15- 2343 23 Застосуємо до нашого прикладу: 1352=18225 13 14=182 18200+25=18225

Піднесення до квадрату цілого числа А, якщо відомий квадрат попередного (А-1) або наступного (А+1) числа. З виразу (А + 1)2 = А2 + 2 А + 1 отримуємо ряд зручних формул: (А + 1)2 = А2 + А + (А + 1) А2=(А + 1)2 - 2 (А + 1) + 1, або А2=(А+1)2-(А + 1)- А

Отримуємо: (18225-2116) 15- 2343 23 Застосуємо до нашого прикладу: 462=2116 452=4 5 100+25=2000+25=2025 462 = (45+1)2 = 2025+45+46=2116

Піднесення до квадрату цілого числа А, якщо відомі числа (А-2)2 або (А+2)2 Піднесення до квадрату цілого числа А, якщо відомі числа (А-2)2 або (А+2)2 виконується за формулами: А2= (А+2)2-(А+(А+2)) 2 = А2+4А+4-4А-4 = А2; А2 = (А-2)2 + (А + (А+2)) 2

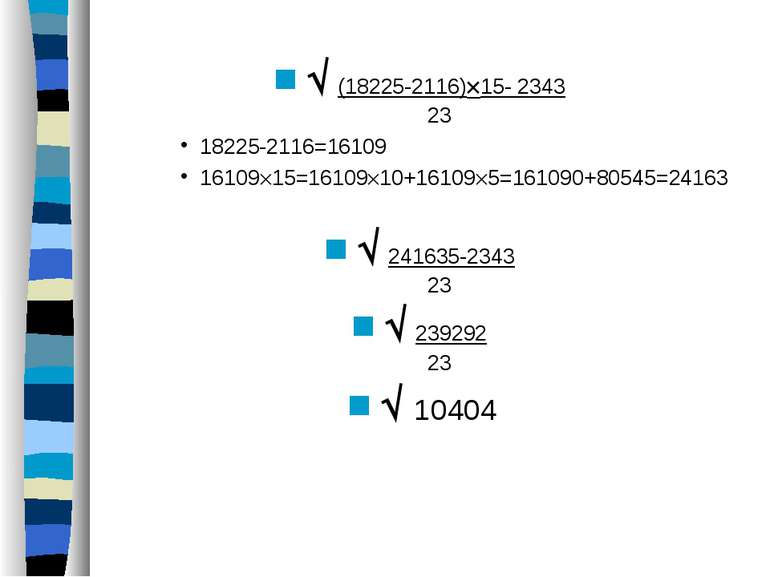
(18225-2116) 15- 2343 23 18225-2116=16109 16109 15=16109 10+16109 5=161090+80545=24163 241635-2343 23 239292 23 10404

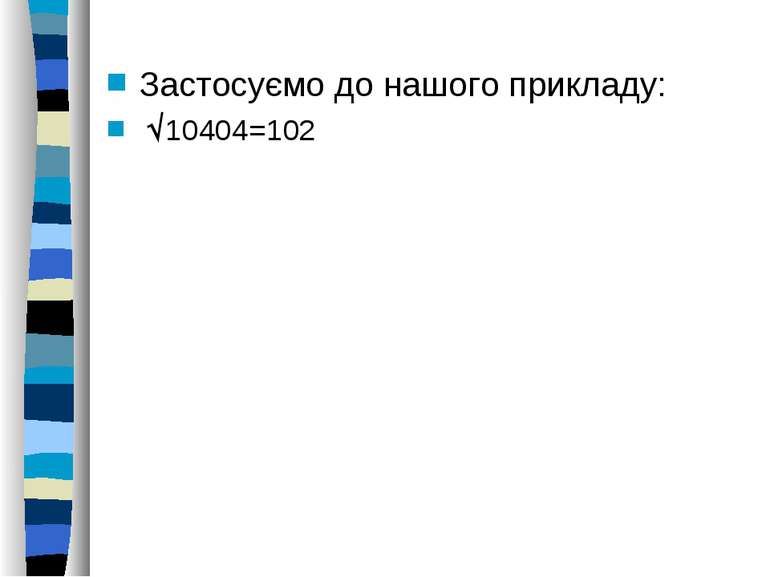
Добування квадратного кореня з числа, що має цілі корені Якщо є число А2 , а А його цілий корінь, то знайти його можна так: Розглянемо суму n послідовних непарних натурвльних чисел: 1+3+5+…+(2n-1)=(1+(2n-1))/2*n=2n/2*n=n2 Таким чином, квадрат натурального числа n дорівнює сумі n непарних послідовних натуральних чисел (починаючи від 1)

Застосуємо до нашого прикладу: 10404=102

Множення «решіткою»

Дякую за увагу