Презентація на тему:
Лінійна нерівність з однією змінною

Матеріали до уроків За підручником «Алгебра. 9 клас» Ю.І. Мальованого, Г.М. Литвиненко, Г.М. Возняк 9 клас Алгебра

Тема 2 Розв’язування лінійних нерівностей і систем нерівностей з однією змінною Лінійна нерівність з однією змінною. Рівносильні нерівності Система (та сукупність) нерівностей з однією змінною Числові проміжки. Переріз і об'єднання проміжків Нерівності, що містять модуль Розв’язування вправ. Самостійна робота Розв’язування систем ( та сукупностей) лінійних нерівностей з однією змінною. Доведення нерівностей Розв’язування вправ. Самостійна робота Розв'язування вправ

Зміст Для роботи виберіть потрібну тему, в якій слід вказати тему уроку. Для переходу між слайдами: 1 клік миші, або використати кнопки керування діями назад на початок вперед на кінець на 1 слайд повернутися (додому) Тема 1. Числові нерівності. Властивості числових нерівностей Тема2. Розв’язування лінійних нерівностей і систем нерівностей з однією змінною Тема 3. Функція. Квадратична функція Тема 4. Квадратичні нерівності та системи рівнянь другого степеня Тема 5. Елементи прикладної математики Тема 6. Арифметична та геометрична прогресії Дл

Пункт 2.1. Нерівності зі змінною Лінійна нерівність з однією змінною та її розв'язок Як розв'язують лінійну нерівність Рівносильні перетворення нерівностей Ілюстрації властивостей Числові проміжки Приклади Лінійна нерівність з однією змінною

Пригадайте Як впливає на правильну числову нерівність: а) додавання до обох її частин одного і того самого числа; б) множення (ділення) обох її частин на одне і те саме додатне число? 2) Закінчіть фразу: Щоб отримати правильну нерівність у результаті множення або ділення обох частин правильної нерівності на одне і те саме від'ємне число, потрібно …

Нерівності зі змінними Крім числових нерівностей, існують нерівності, які містять змінні – одну або декілька. Наприклад: x+12x+5 – нерівності першого степеня; x2-x10 – нерівність першого степеня з двома змінними.

Надаючи змінній у нерівності зі змінною певного числового значення, отримуємо числову нерівність. Наприклад: Надамо змінній х у нерівності х+4

Лінійна нерівність з однією змінною та її розв’язок Приклади: а) 2х+4>0 (a=2, b=4); б) 3x-2

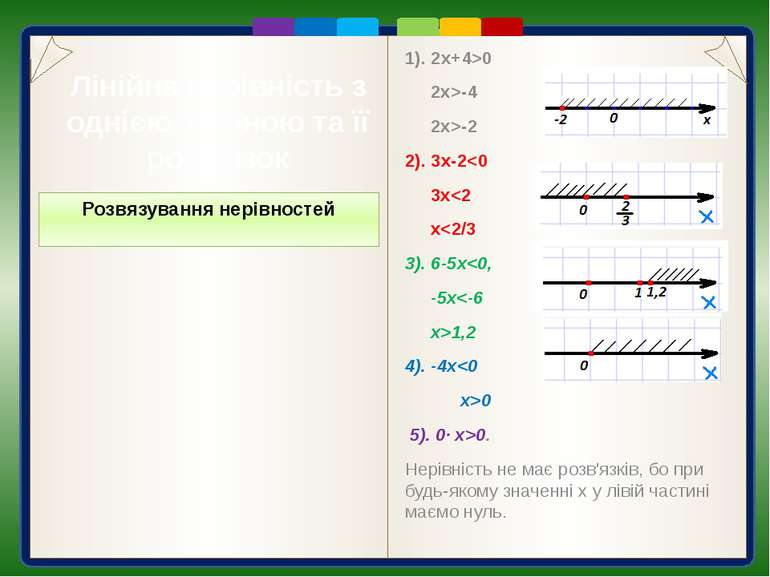
Лінійна нерівність з однією змінною та її розв’язок Приклад: а) Число 3 є розв'язком нерівності 2х+4>0, бо при х=3 числова нерівність 2·3+4=6+4=10>0 – правильна. Число -1 також є розв'язком даної нерівності, бо 2·(-1)+4=-2+4=2>0. Розв'язком лінійної нерівності з однією змінною називають значення змінної, підставивши яке вдану нерівність, отримують правильну числову нерівність. Кажуть, що це значення змінної задовольняє дану нерівність.

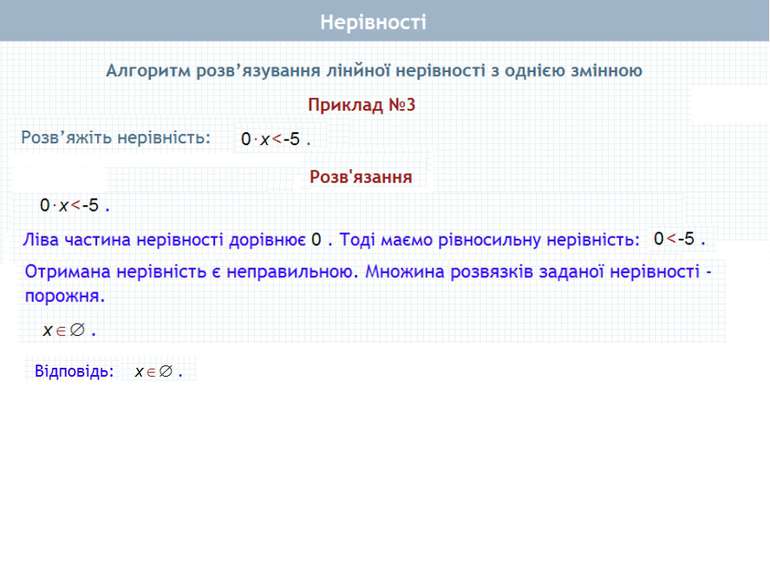
Лінійна нерівність з однією змінною та її розв’язок Як розв'язують лінійну нерівність Розв'язати нерівність – означає знайти всі її розв'язки. Дві нерівності, що мають одні і ті самі розв'язки, називаються рівносильними.

Лінійна нерівність з однією змінною та її розв’язок Основні властивості нерівностей зі змінними 1. Якщо з однієї частини нерівності перенести в другу будь-який доданок з протилежним знаком, то отримаємо нерівність, рівносильну даній Наприклад, перенісши у нерівності 2х+4>0 доданок 4 з протилежним знаком у праву частину, отримаємо 2x>-4, яка рівносильна даній.

Лінійна нерівність з однією змінною та її розв’язок Основні властивості нерівностей зі змінними 2. Якщо обидві частини нерівності помножити (поділити) на одне й те саме додатне число, то отримаємо нерівність, рівносильну даній Наприклад, помноживши обидві частини нерівності 2х+4>0 на число 5, отримаємо 10x+20>0, яка рівносильна даній.

Лінійна нерівність з однією змінною та її розв’язок Основні властивості нерівностей зі змінними 3. Якщо обидві частини нерівності помножити (поділити) на одне й те саме від'ємне число і змінити знак нерівності на протилежний, то отримаємо нерівність, рівносильну даній Наприклад, помноживши обидві частини нерівності 2х+4>0 на число -5 і помінявши знак нерівності на протилежний , отримаємо -10x-20

Первинне закріплення вивченого матеріалу

Лінійна нерівність з однією змінною та її розв’язок 1). 2x+4>0 2x>-4 2x>-2 2). 3x-2

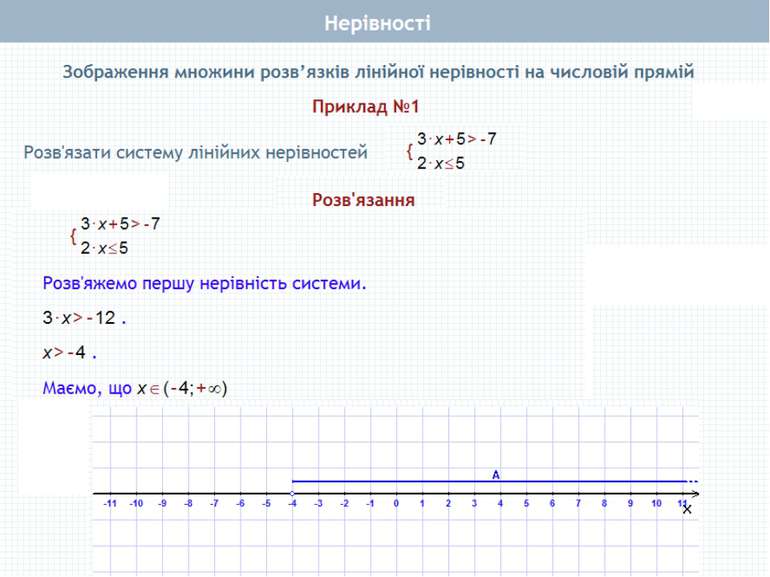
Лінійна нерівність з однією змінною та її розв’язок Приклади: а) 2х+4>0, x>-2 або (-2; ∞) – читають: «Проміжок від -2 до нескінченності»; б) 3x-2

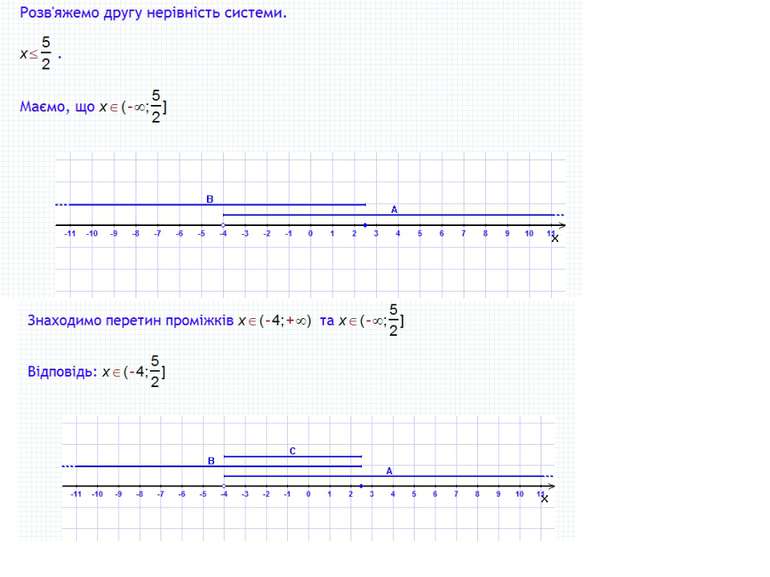
Лінійна нерівність з однією змінною та її розв’язок Число, яке належить проміжку, зображують затушованим кружечком. Зображений числовий проміжок позначають так: [-2;∞), читають: “Проміжок від -2, включаючи -2, до нескінченності” і записують у вигляді нерівності x≥-2. Числові проміжки Числовий проміжок (-∞;∞) називають числовою прямою. Це множина всіх дійсних чисел.

Лінійна нерівність з однією змінною та її розв’язок Числовий проміжок, зображений на рисунку, позначають так: (-∞; ], читають: “Проміжок від мінус нескінченності до включно”. Відповідна числова нерівність має вигляд x≤ . Числові проміжки

Лінійна нерівність з однією змінною та її розв’язок Знаки ≥ і ≤ називають знаками нестрогої нерівності і читають так: ≥ - більше або дорівнює (не менше) ≤ - менше або дорівнює (не більше) Числові проміжки

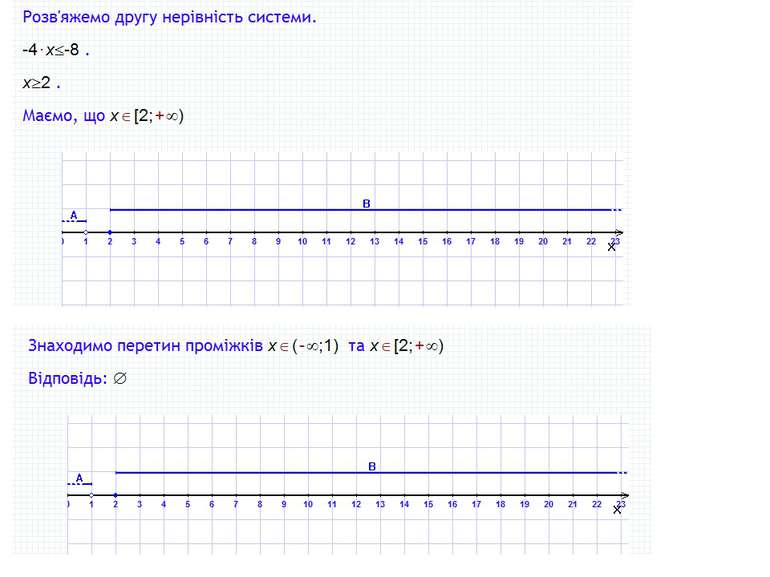
Лінійна нерівність з однією змінною та її розв’язок Якщо число х є одночасно розв'язком нерівностей х>-2 і х

Лінійна нерівність з однією змінною та її розв’язок Числовий проміжок, що відповідає подвійній нерівності -2≤x≤1 зображають так, як на рис. і записують: [-2; 1]. Числові проміжки

Лінійна нерівність з однією змінною та її розв’язок Числовий проміжок, що відповідає нерівності a

Лінійна нерівність з однією змінною та її розв’язок Належність числа певній числовій множині позначають знаком . Запис х [-2; 1] означає, що х є будь-яким числом з проміжку [-2; 1]. Розв'язок нерівності 2x+4>0 можна записати так: x>-2 або x (-2; ∞). Числові проміжки