Презентація на тему:
Інтеграл та його застосування.

Тема. Інтеграл та його застосування. Мета. Узагальнити знання й уміння учнів з теми, показати можливість застосування інтеграла в різних галузях фізики, економіки, техніки. Вчити бачити єдину математичну модель в різних ситуаціях; сприяти розширенню кругозору учнів, світогляду. Зміцнити знання з ІКТ. Спонукати учнів щодо підготовки до ДПА. Працювати над поняттями: інтеграція у промисловості, інтеграція у спільноту, продуктивність праці. Розвивати самостійність, працьовитість, наполегливість, відповідальність. Виховувати інтерес до науки, вміння раціонально використовувати робочій час, об’єктивно оцінювати результати своєї праці, комуникативні навички. Застосовувати здоров’язберігаючі технології.

Очікувані результати: учні повинні розуміти зв’язок інтеграла з реальними процесами життя; уміти застосовувати інтеграл під час розв’язування прикладних задач вміти працювати з програмою GRAN, GRAN2D.

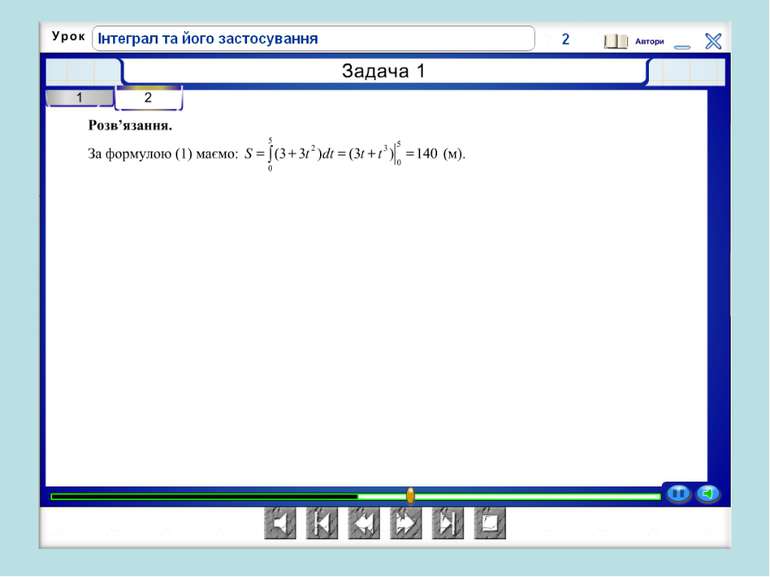
Сьогодні завершуємо вивчати тему “Інтеграл та його застосування”. Урок передує контрольній роботі. Тож, підсумкуємо вивчене. Ми з вами познайомилися з другим поняттям математичного анілізу без якого не збудувати сучасного будинка, космічного корабля, субмарини. Поняття інтегралу з'явилося в результаті практичної діяльності людини, використовується сьогодні в самих різних сферах науково-практичної діяльності людини, а саме: фізиці, хімії, біології, механіці, економіці, філології і т.д. Тому на уроці ми будемо розв'язувати задачі прикладного характеру, що допоможе зрозуміти місце і роль математики в сучасному світі.

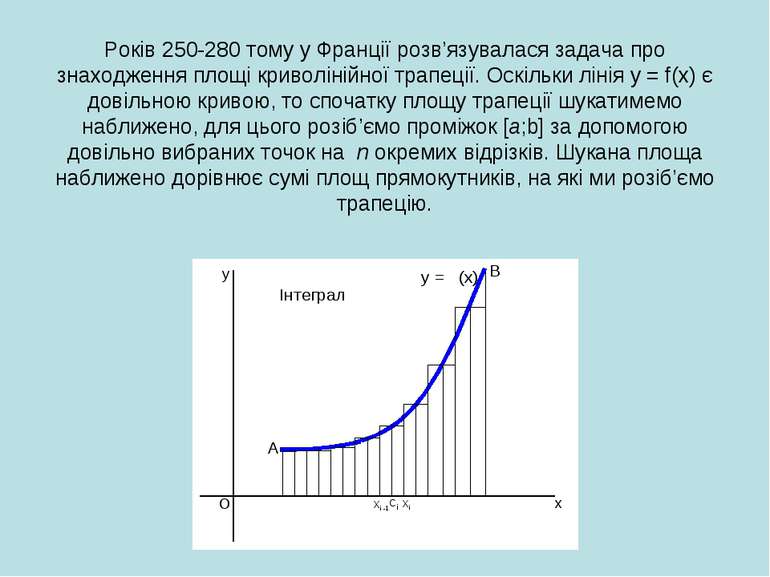
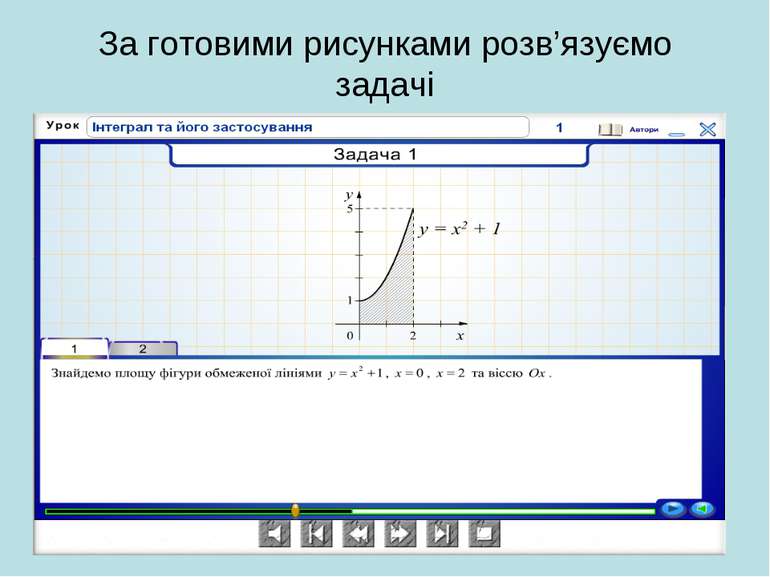
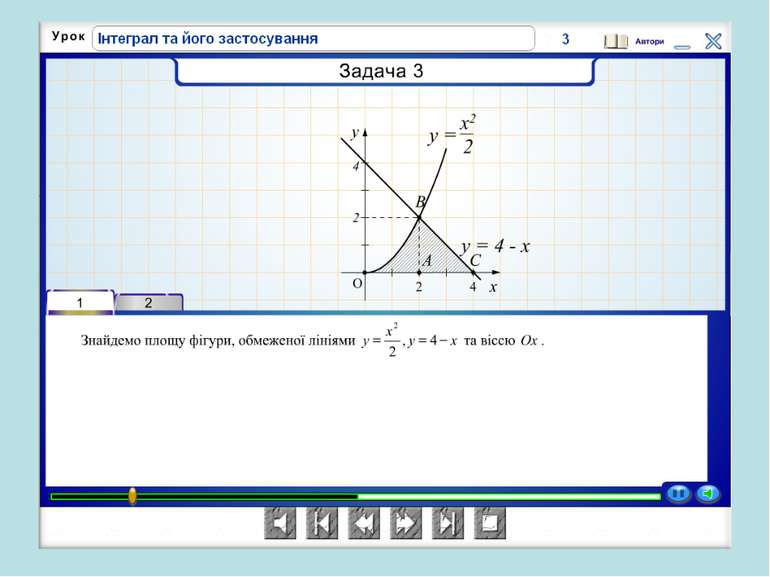
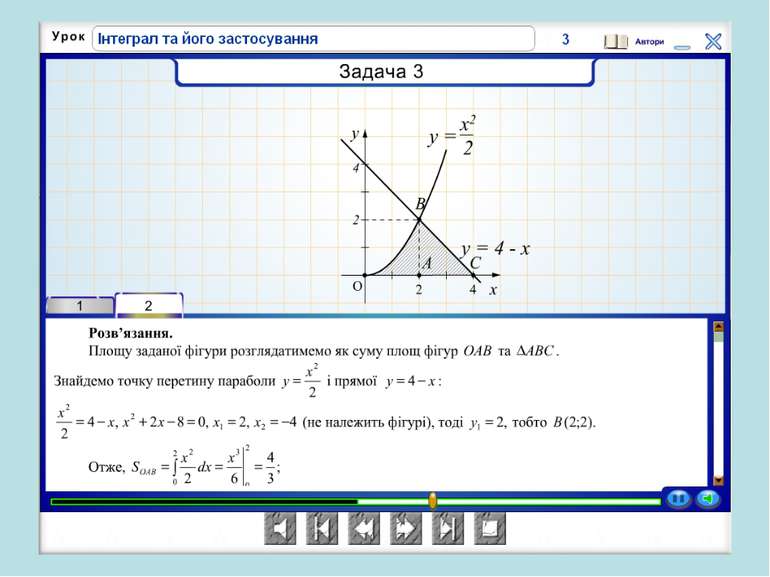
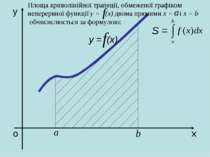
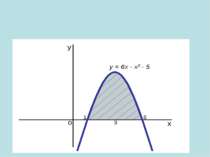
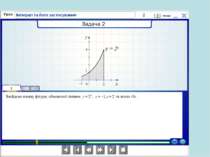
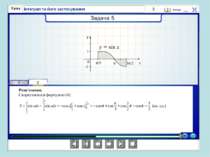
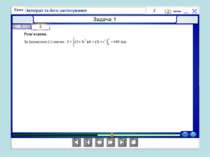
Років 250-280 тому у Франції розв’язувалася задача про знаходження площі криволінійної трапеції. Оскільки лінія у = f(x) є довільною кривою, то спочатку площу трапеції шукатимемо наближено, для цього розіб’ємо проміжок [а;b] за допомогою довільно вибраних точок на п окремих відрізків. Шукана площа наближено дорівнює сумі площ прямокутників, на які ми розіб’ємо трапецію.

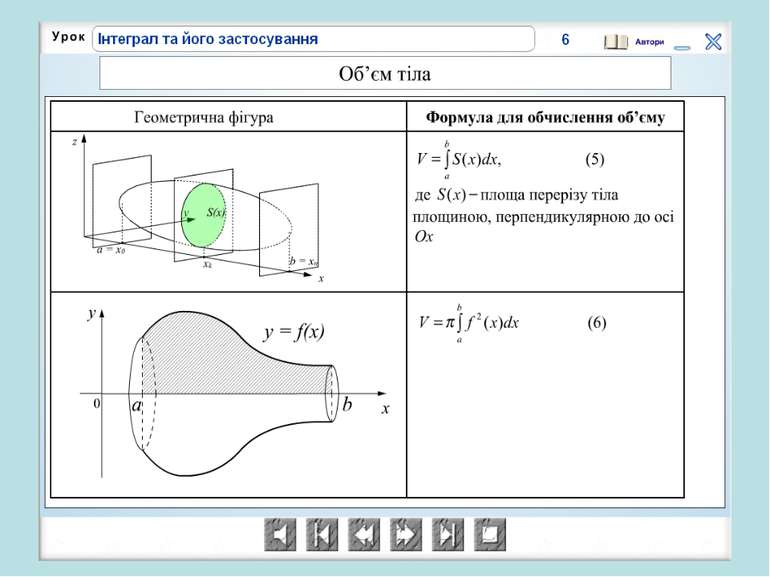
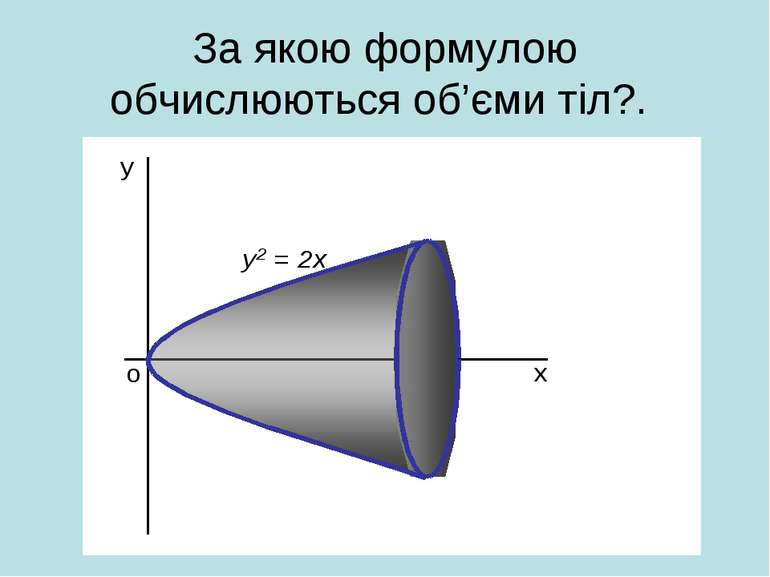
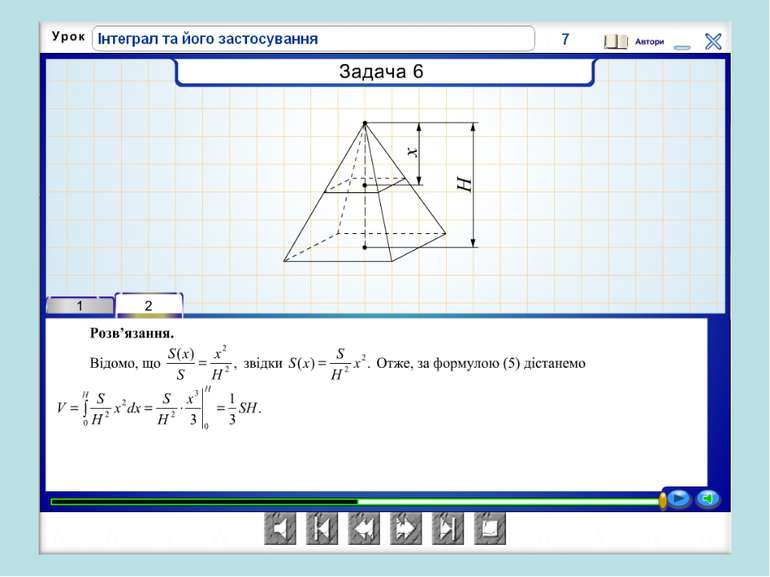
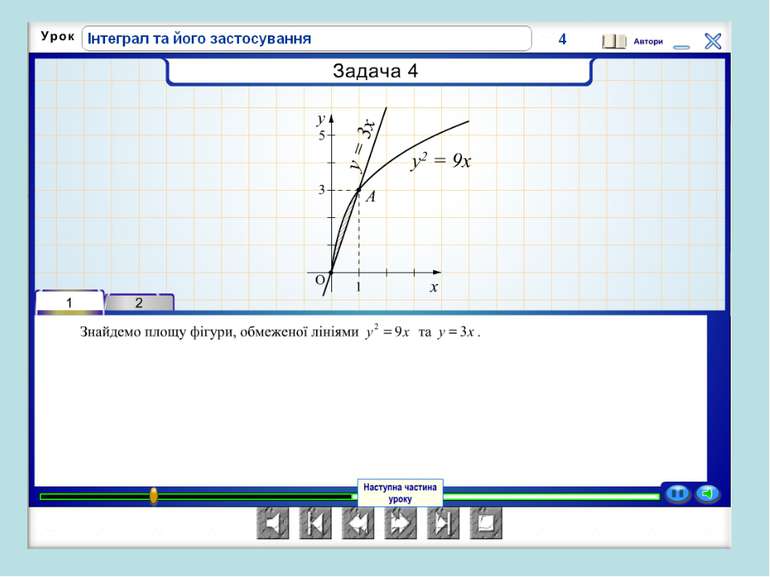
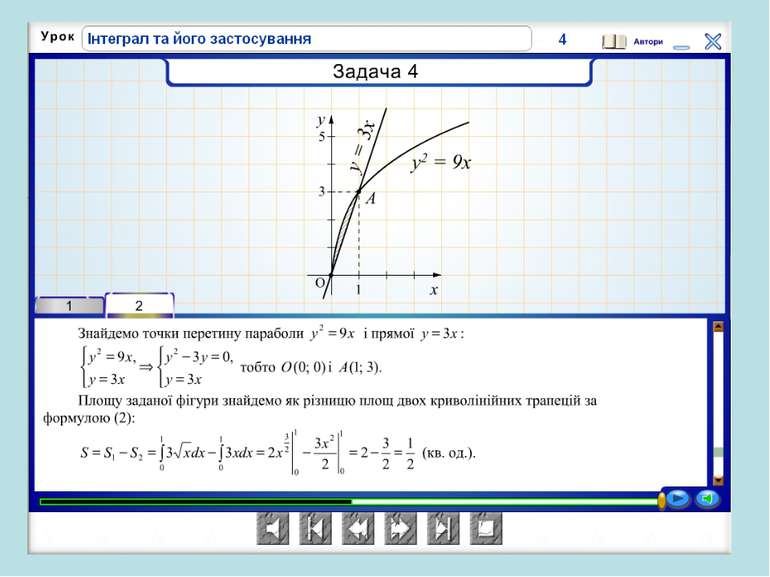
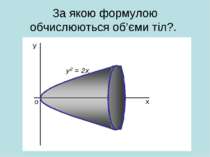
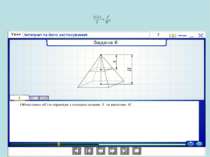
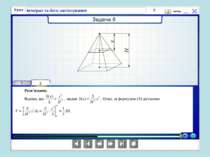
В Італії розв’язувалася задача про знаходження об’єму тіла, в Азії – про визначення тиску води в ариках, в Іспанії-визначали роботу сили при переміщенні заряду q із точки А в точку В. Країни різні, задачі різні, але підхід однаковий.

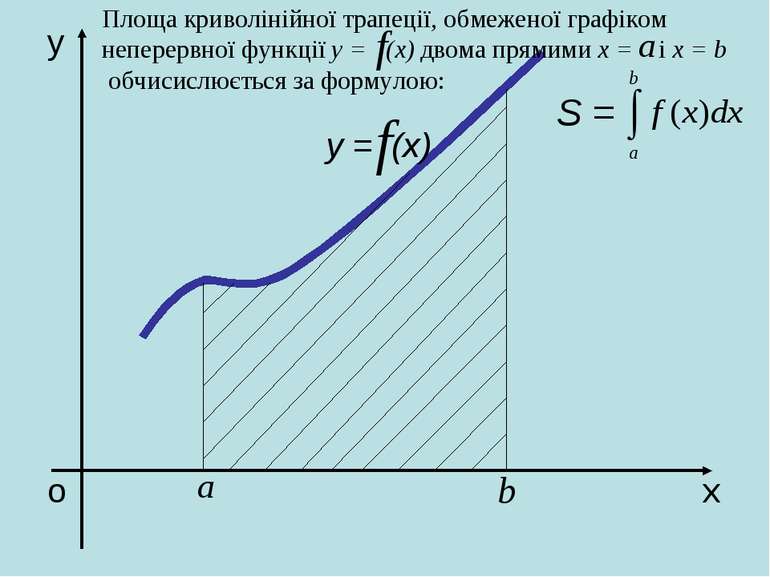
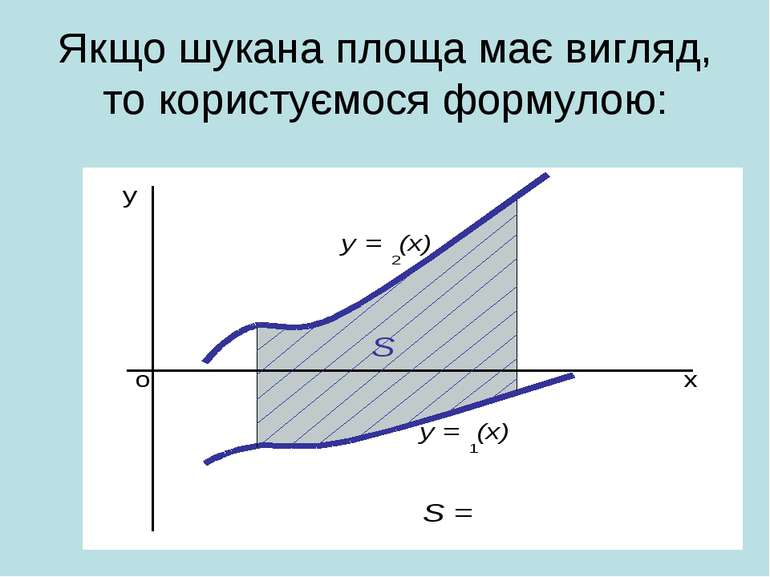
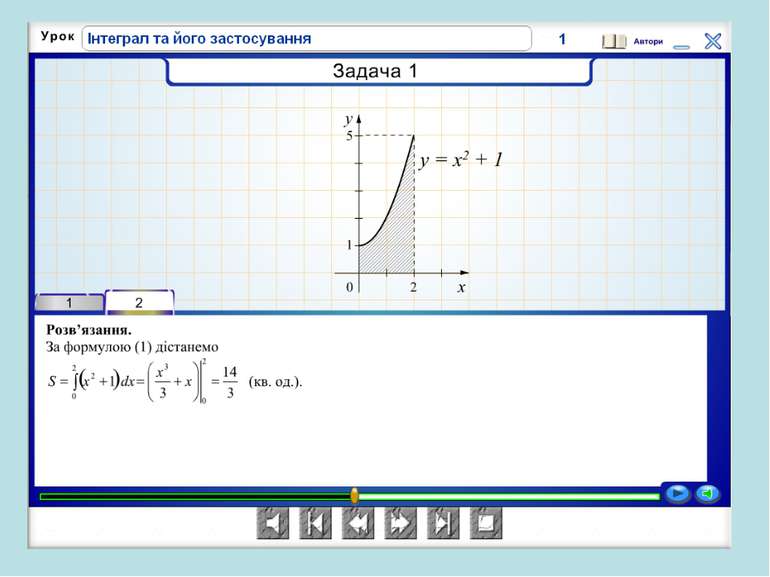
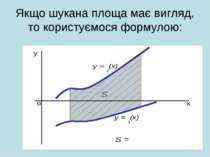
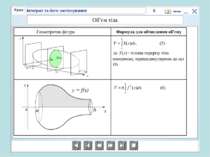
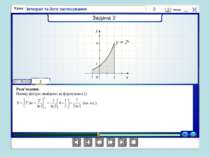
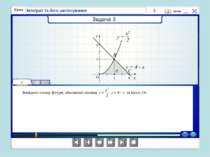
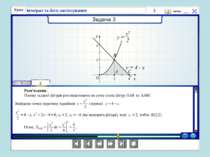
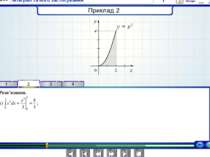
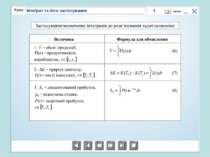
о х у у = (х) Площа криволінійної трапеції, обмеженої графіком неперервної функції у = (х) двома прямими х = і х = b обчисислюється за формулою: S =

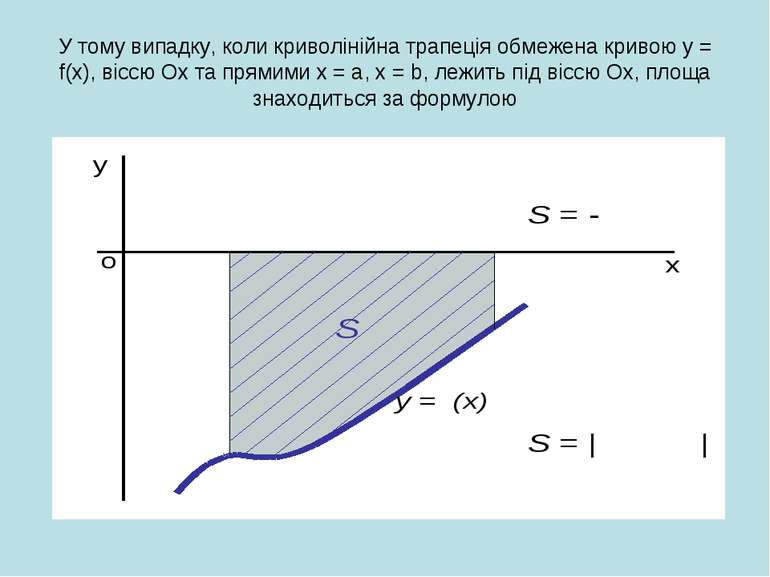
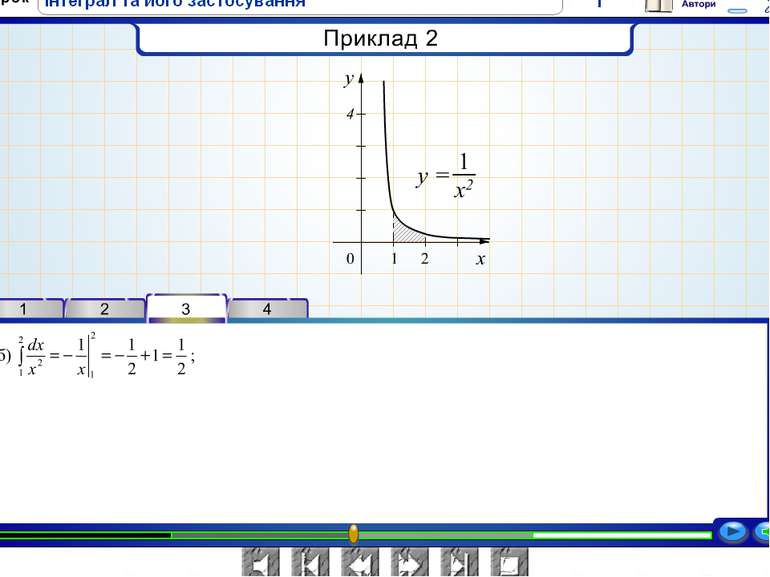
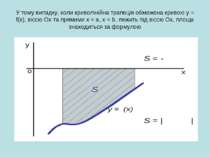
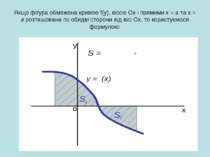
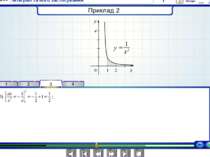
У тому випадку, коли криволінійна трапеція обмежена кривою у = f(x), віссю Ох та прямими х = a, x = b, лежить під віссю Ох, площа знаходиться за формулою

Якщо фігуру можна розбити на декілька частин, то її площа буде дорівнювати сумі цих частин.

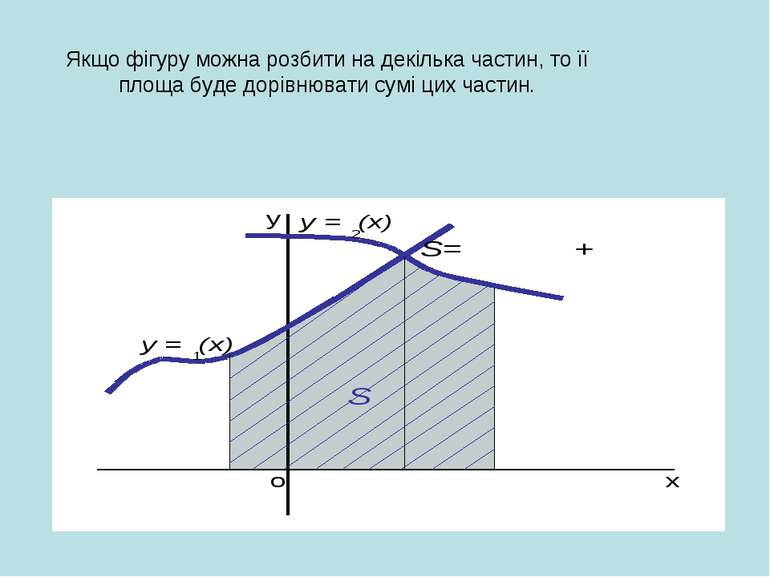
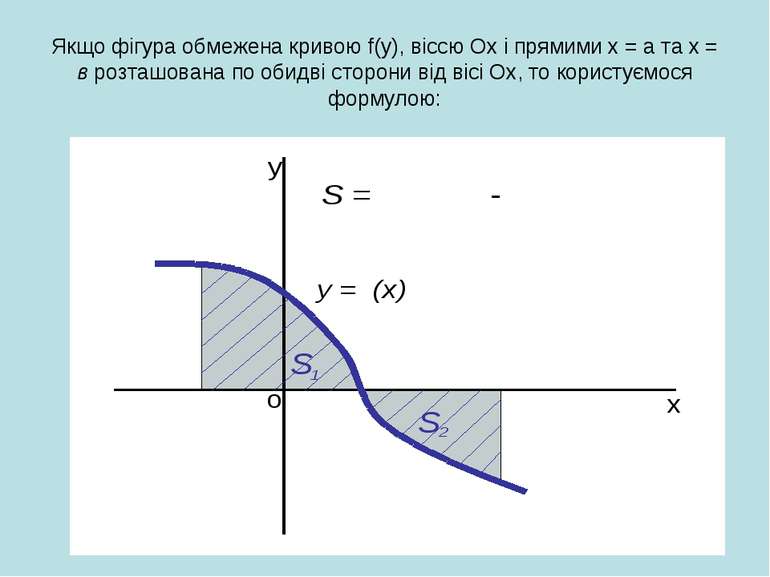
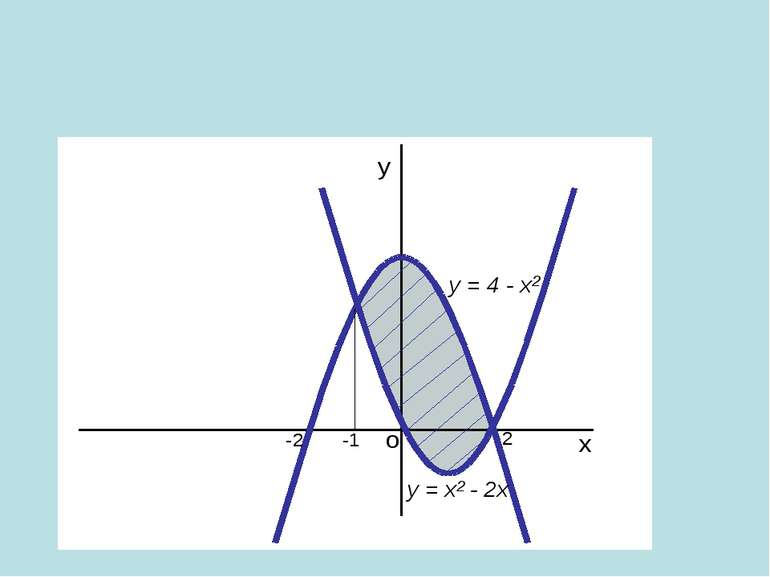
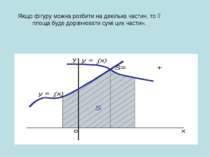
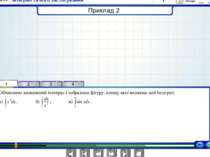
Якщо фігура обмежена кривою f(y), віссю Ох і прямими х = а та х = в розташована по обидві сторони від вісі Ох, то користуємося формулою:

Якщо шукана площа має вигляд, то користуємося формулою:

Записати за допомогою інтегралів площі фігур

За якою формулою обчислюються об’єми тіл?.

Інтеграція у промисловості Агропромисло ва інтегра ція — поєднання сільськогосподарського виробництва з переробною промисловістю та іншими галузями господарства. Слово «інтеграція» походить від латинського й означає поєднання окремих частин в єдине ціле. В широкому розумінні під інтеграцією розуміють посилення економічних і виробничих зв’язків між різними країнами (прикладом таких зв’язків є створення ЄС і СНД), окремими сферами і суміжними галузями, а також між різними підприємствами, організаціями та іншими суб’єктами ринку. Матеріал з Вікіпедії. Наведіть приклади інтеграції молоді у спільноти.

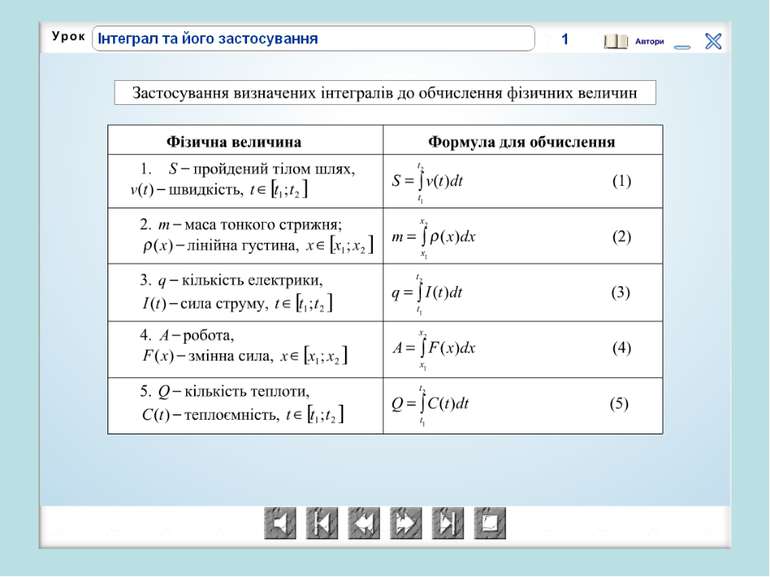
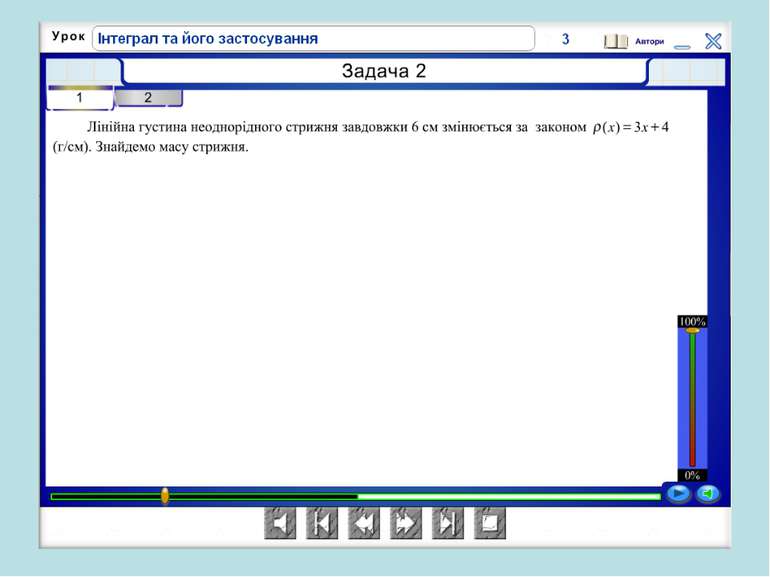
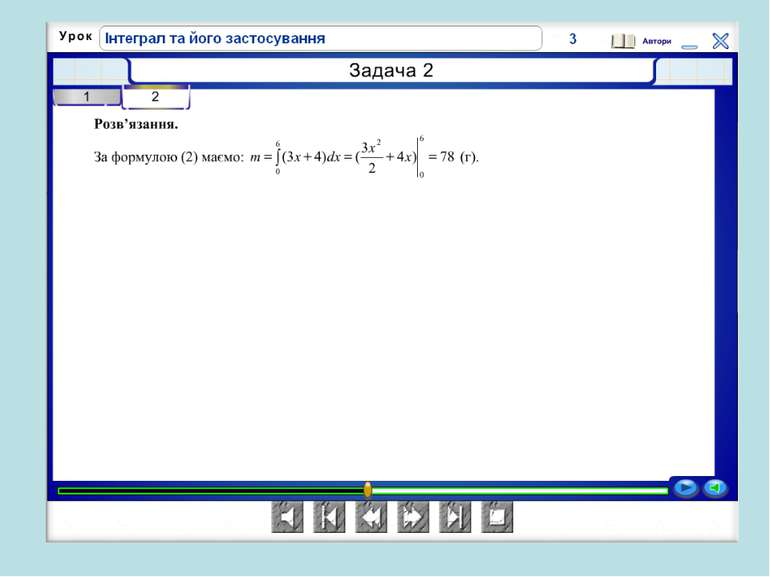
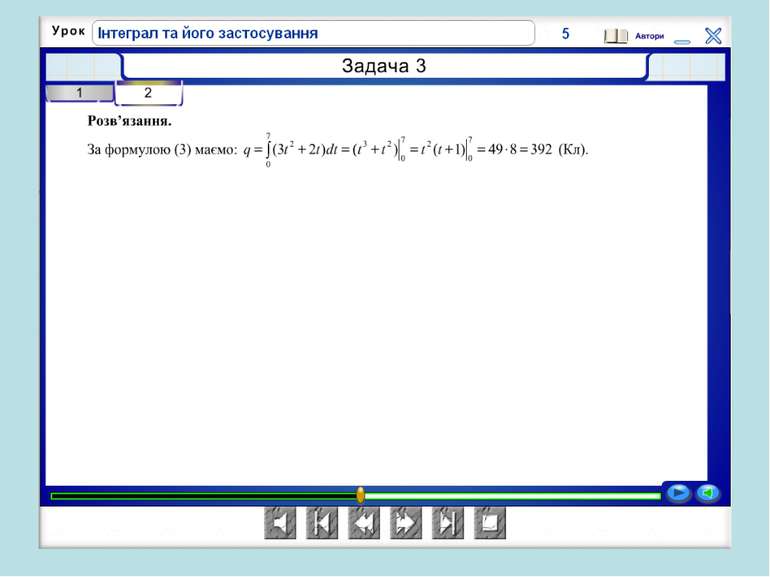
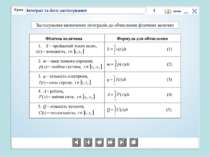
Бліц-опитування Установіть відповідність між формулою і фізичними величинами, які вона пов’язує. 1. s = ν(t) ∙ t A. Робота і потужність 2. A = N(t) ∙ t Б. Сила струму і електричний заряд 3. q = I(t) ∙ t В. Швидкість руху і переміщення 4. Q = c(t) ∙ t Г. Лінійна густина і маса стрижня Д. Кількість теплоти і теплоємність За кожну вірну відповідь одержуємо 1 бал.

Правильні відповіді на бліц-опитування

За готовими рисунками розв’язуємо задачі

Задача 5. Знайти площу фігури, обмежену лініями: у = sinx, прямими х = 0, x=2π.

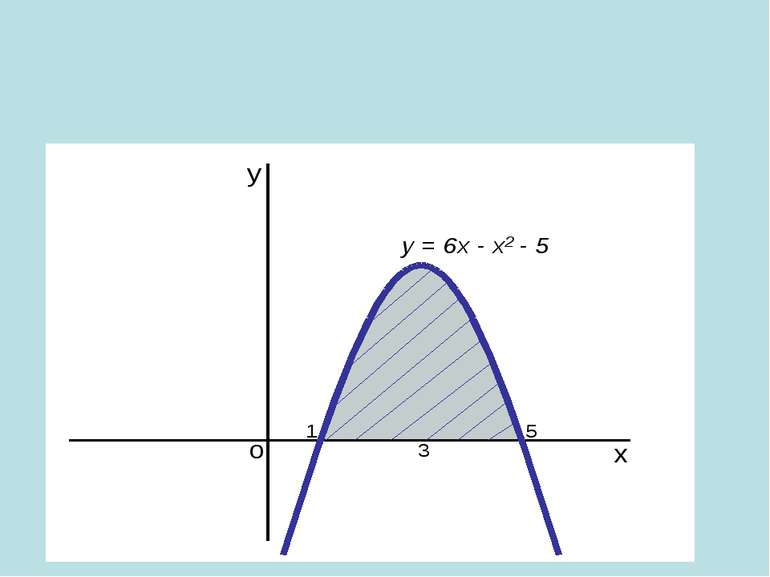
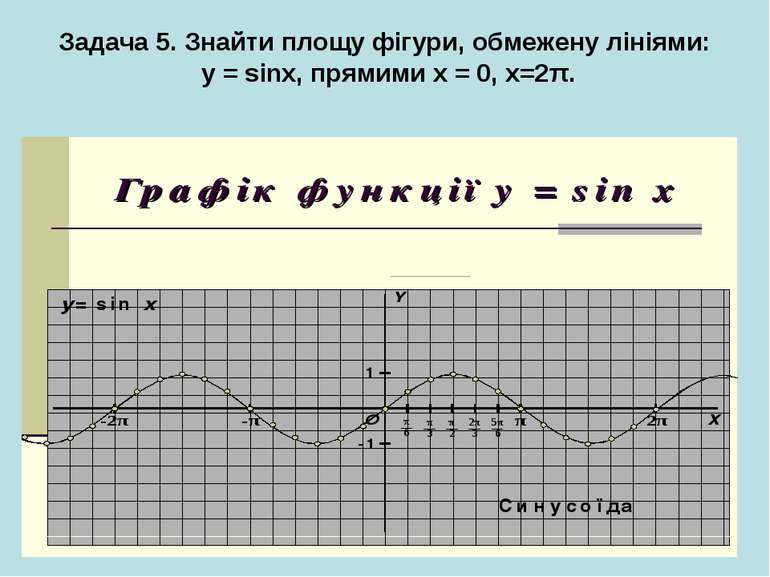
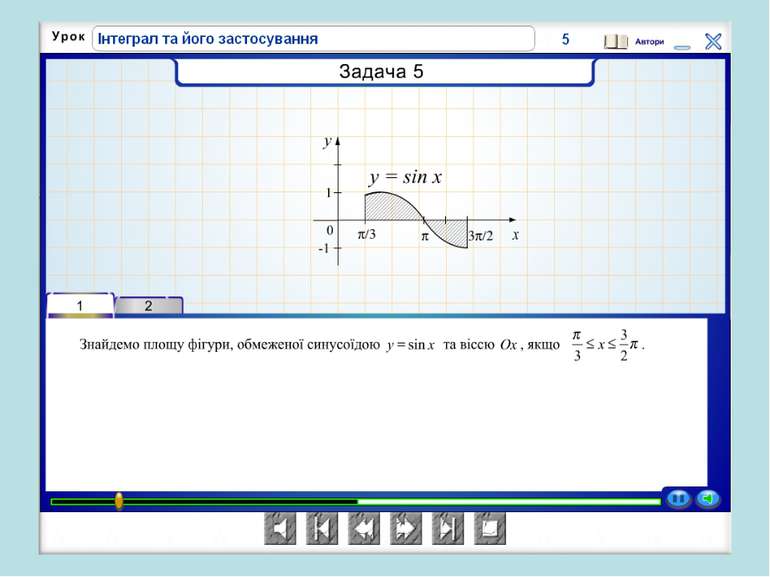
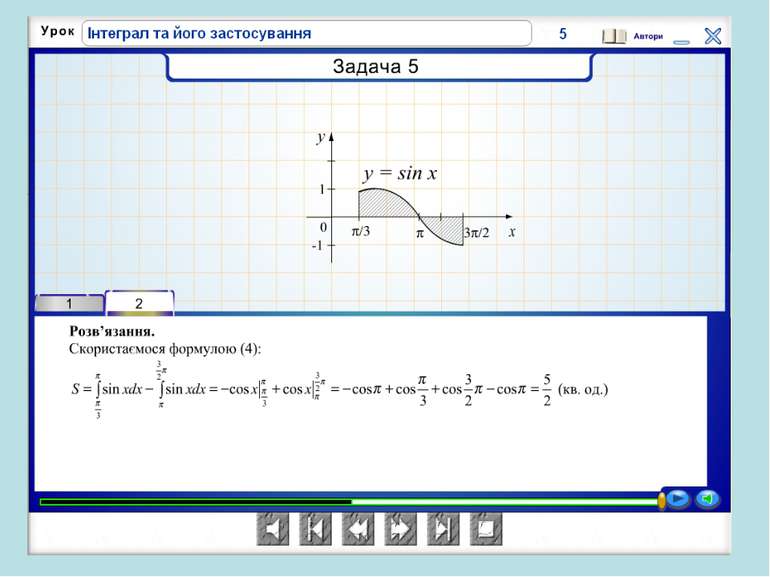
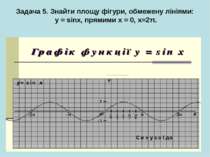
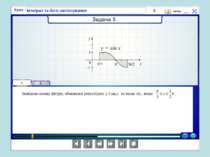
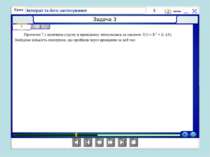
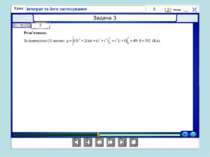
Проблемна ситуація «Працюй мозком»! Площа фігури не може дорівнювати 0, оскільки вона існує. Ми не виконали перевірку функції на додатність, а частина графіка від π до 2π лежить під віссю Ох, отже, треба:

Самостійна робота учнів Учні розв’язують задачі, виконують взаємоперевірку за готовими розв’язками (на слайдах).

Обов’язково розв’язати приклади а і в (б і г за бажанням)

Лист оцінювання

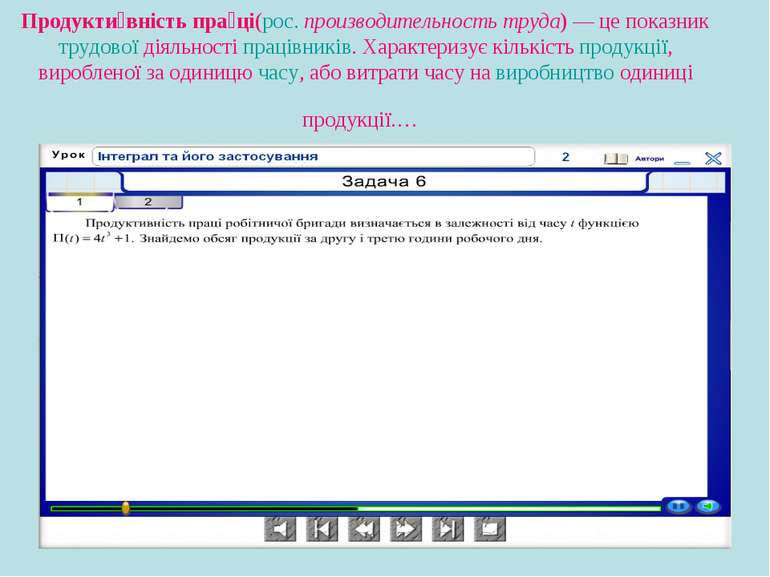
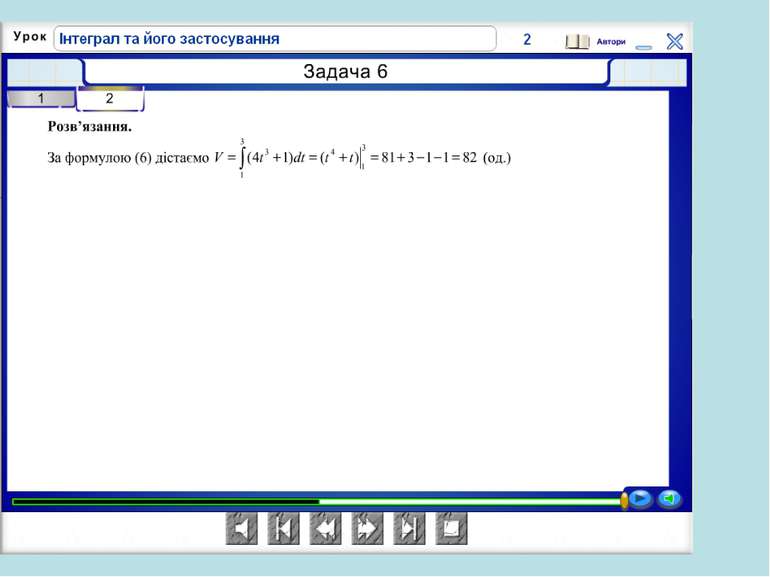
Продукти вність пра ці(рос. производительность труда) — це показник трудової діяльності працівників. Характеризує кількість продукції, виробленої за одиницю часу, або витрати часу на виробництво одиниці продукції.…

Інструктаж з безпеки життєдіяльності Вимоги безпеки під час роботи Заборонено ходити по комп’ютерному класу, голосно розмовляти. Виконувати слід тільки зазначене учителем завдання. Категорично заборонено виконувати інші роботи. На клавіші клавіатури потрібно натискати плавно, не припускаючи ударів. Користуватися друкувальним пристроєм дозволяється тільки у присутності викладача або лаборанта. Заборонено запускати ігрові програми. У випадку виникнення неполадок, треба повідомити викладача або лаборанта. Вимоги безпеки після закінчення роботи ─ Про хиби та неполадки, помічені під час роботи, слід зробити записи у відповідних журналах. ─ На робочому місці не потрібно залишати зайвих предметів. Вимоги безпеки в аварійних ситуаціях. При появі незвичайного звуку або вимкнення апаратури потрібно негайно припинити роботу й довести це до відома вчителя або лаборанта.

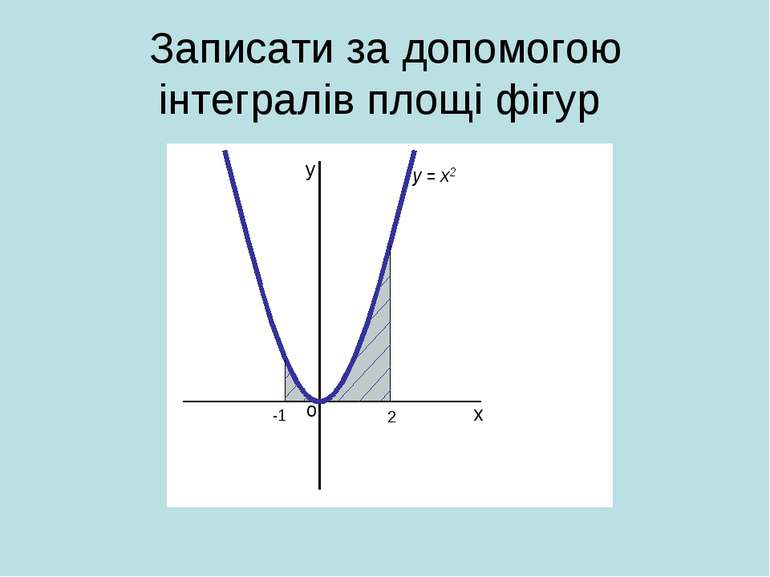
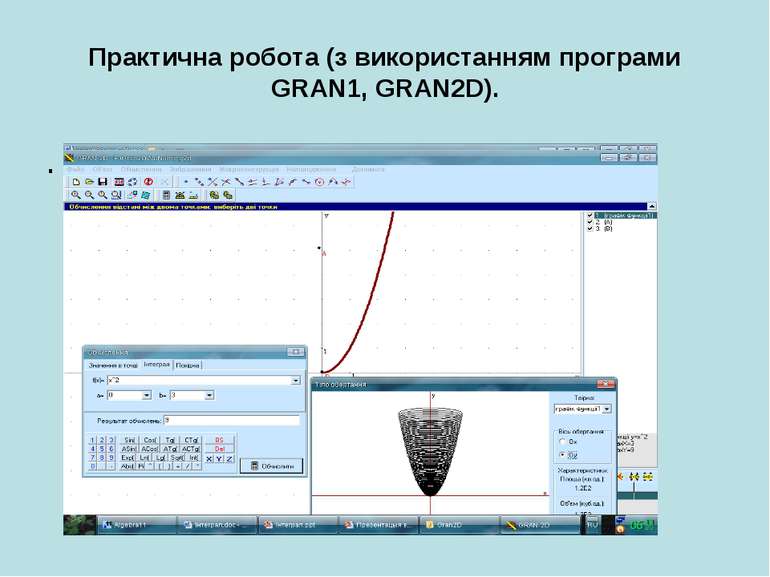
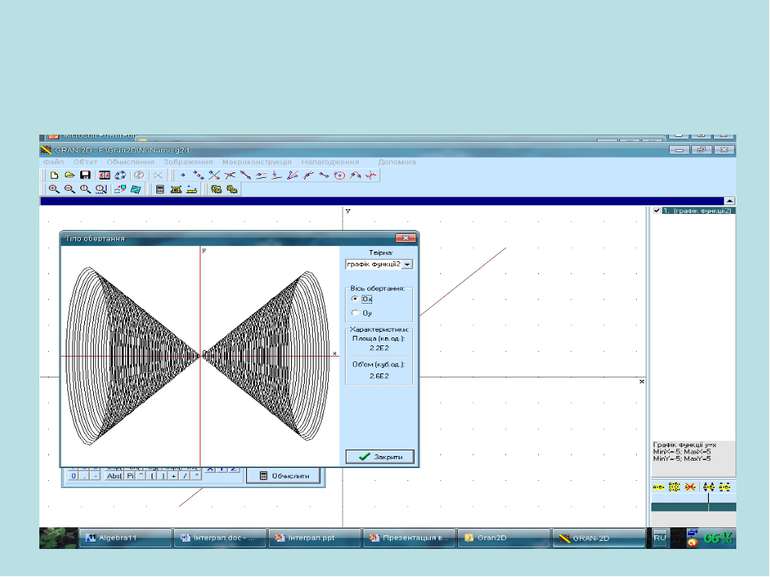
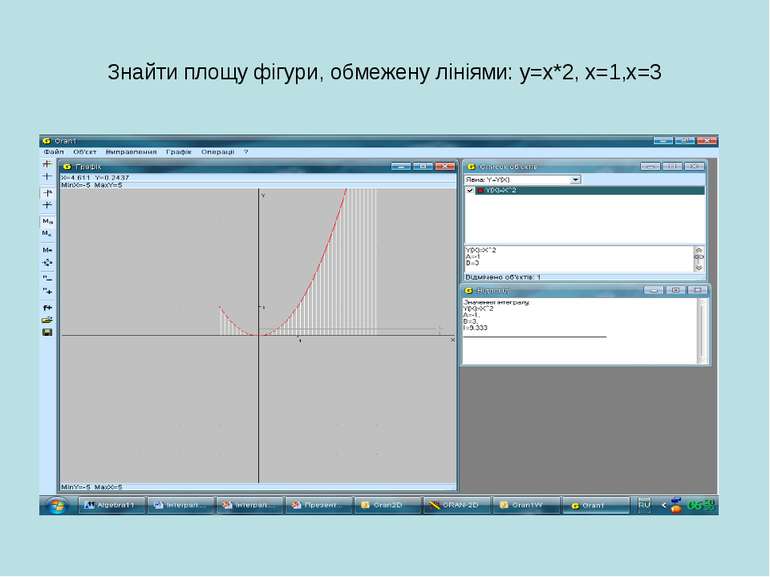
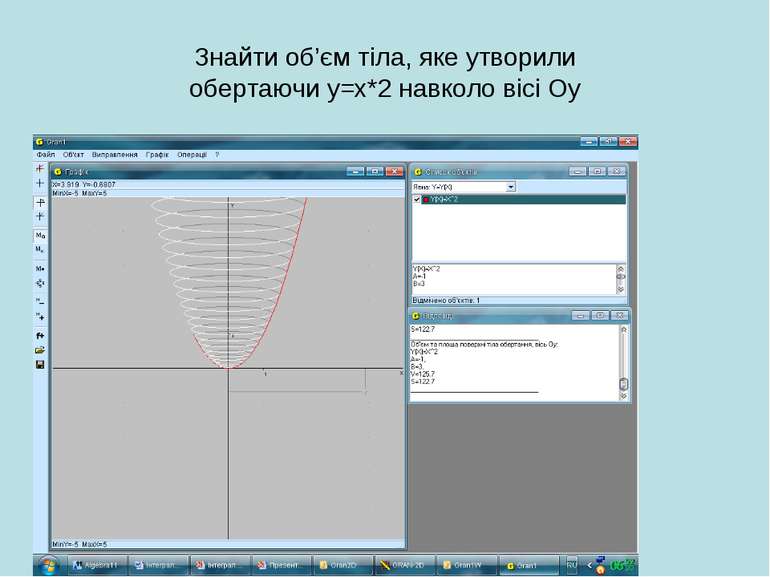
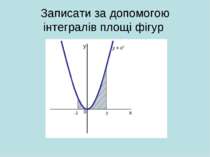
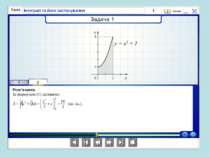
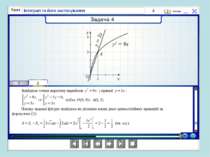
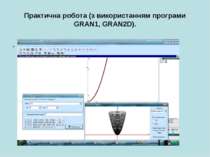
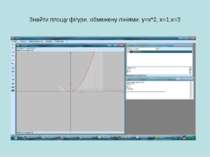
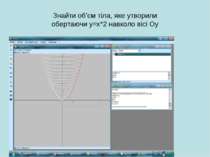
Практична робота (з використанням програми GRAN1, GRAN2D). Побудувати та обчислити площу фігури, обмежену лініями: y = x*x, x = -1, x = 3. Обчислити об’єм тіла, утвореного обертанням навколо осі Оу фігури, обмеженої лініями: y = x*x, y = 3.

Інструктивна картка Алгоритм виконання практичної роботи Відкрити програму GRAN1. Створити новий об’єкт. Побудувати фігуру та обчислити її площу. Побудувати тіло та обчислити площу поверхні і його об’єм.

Практична робота (з використанням програми GRAN1, GRAN2D). .

Знайти площу фігури, обмежену лініями: у=х*2, х=1,х=3

Знайти об’єм тіла, яке утворили обертаючи у=х*2 навколо вісі Оу

КОМПЛЕКС ВПРАВ ДЛЯ ОЧЕЙ Вправи виконуються сидячи, відвернувшись від екрана при ритмічному подиху, із максимальною амплітудою руху очей. Закрити очі, сильно напружуючи очні м’язи, на рахунок 1-4, потім розкрити очі, розслабивши м’язи очей, подивитися вдалину на рахунок 1-6. Повторити 2 рази. Звести очі до перенісся і затримати погляд на рахунок 1-4. До втоми ока не доводити. Потім подивитися вдалину на рахунок 1-6. Повторити 2 рази. Не повертаючи голови, подивитися праворуч і зафіксувати погляд на рахунок 1-4, потім подивитися вдалину прямо на рахунок 1-6. Аналогічно проводяться вправи, але з фіксацією погляду, вліво, нагору й вниз. Повторити 2 рази. Перевести погляд швидко по діагоналі: праворуч нагору – ліворуч униз, потім прямо вдалину на рахунок 1-6; потім ліворуч нагору – праворуч униз і подивитися вдалину на рахунок 1-6. Повторити 2 рази.

VI. Підсумки уроку Рефлексія. Інтерактивна вправа «Мікрофон». Продовжити речення: «Сьогодні на уроці я …».

Домашнє завдання Готуємося до ДПА . Збірник завдань для ДПА з математики, 11 клас.2012 рік. Автори: О.С. Істер, О.І.Глобін, І.Є.Панкратова. 1.Варіант 2 (завдання 2.3) 2.Варіант 3 (завдання 2.3) 3.Варіант 8 (завдання 2.3) 4.Варіант 10 (завдання 2.3) 6. Варіант 11 (завдання 3.1)

Дякую усім за увагу! З повагою, ваш викладач.