Презентація на тему:
Інтеграл та його застосування

Інтеграл та його застосування. Виконала вчитель математики Томчук Тетяна Ярославівна

Епіграф Недостатньо лише отримати знання, треба знайти їм застосування. Недостатньо тільки бажати, треба творити.

Математичний диктант Знайти похідну даної функції (3 ln x)’ (sin 2x)’ (2)’ (2 cos 2x)’ (2х)’ =2 = 2Cos2x = 0 = 42x =-2Sin2x = 48(2x-5)²

Знайти первісну F(sin 2x) =7x

Інтерактивна вправа «мозковий штурм» Яка фігура називається криволінійною трапецією?

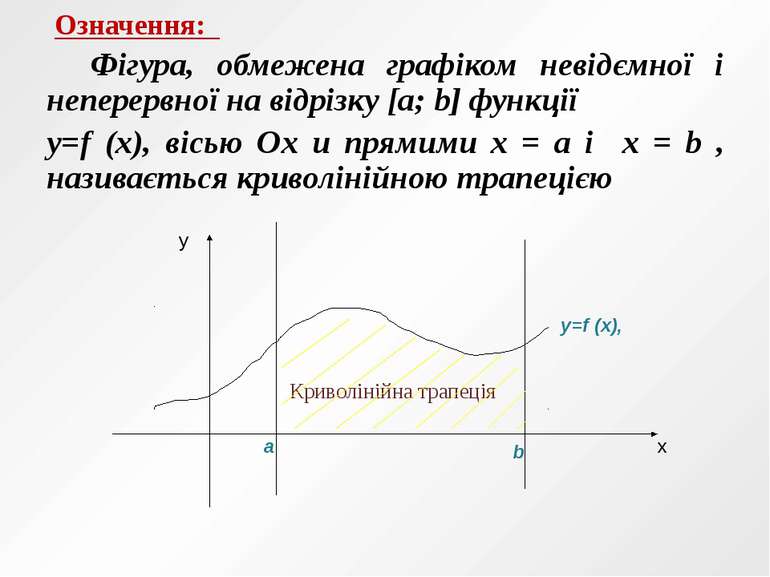
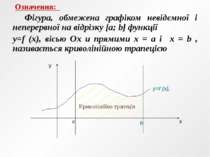
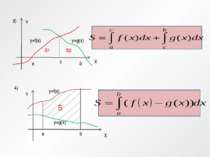
Означення: Фігура, обмежена графіком невідємної і неперервної на відрізку [a; b] функції y=f (x), вісью Ох и прямими х = а і х = b , називається криволінійною трапецією x y y=f (x), а b Криволінійна трапеція

Як обчислити площу криволінійної трапеції?

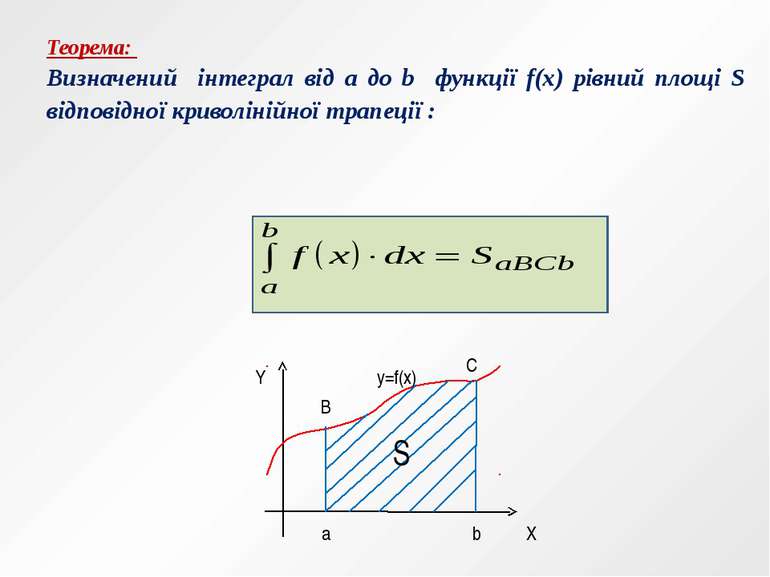
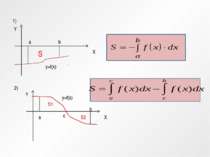
Теорема: Визначений інтеграл від a до b функції f(x) рівний площі S відповідної криволінійної трапеції : Y X а b y=f(x) B C S

Як обчислити площу фігури обмеженої лініями ?

a b y=f(x) S 1) 2) y=f(x) a b c S1 S2 Y X Y X

Y X a b y=f(x) 3) 4) Y X y=f(x) a b c S1 S2 y=g(x) y=g(x) S

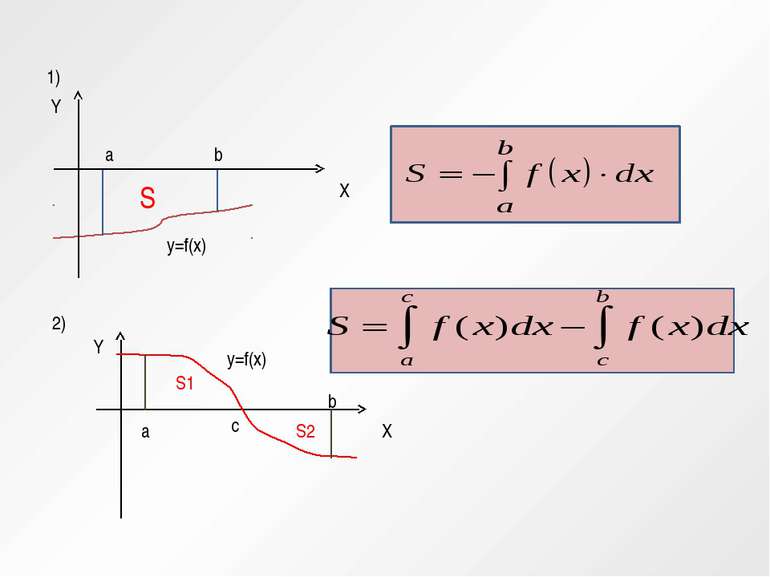
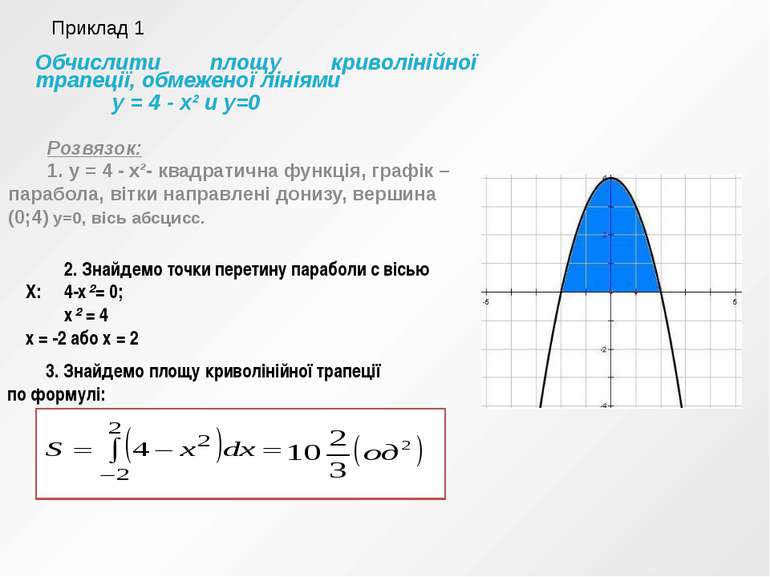
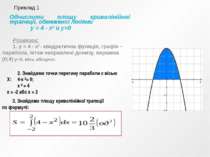
Обчислити площу криволінійної трапеції, обмеженої лініями у = 4 - х² и у=0 Розвязок: 1. у = 4 - х²- квадратична функція, графік – парабола, вітки направлені донизу, вершина (0;4) у=0, вісь абсцисс. 2. Знайдемо точки перетину параболи с вісью Х: 4-х²= 0; х² = 4 х = -2 або х = 2 3. Знайдемо площу криволінійної трапеції по формулі: Приклад 1

Як обчислити об’єм фігури обертання за допомогою інтеграла?

Використання інтеграла для обчислення об’єму

ОБЧИСЛИТИ ІНТЕГРАЛИ

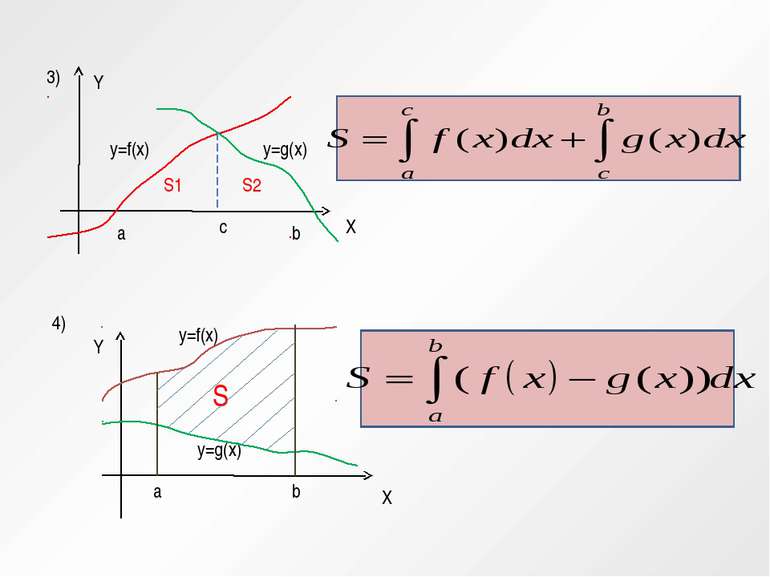
обчислити площі плоских фігур, обмежених лініями: у=х², у=4 у=х³, віссю Ох і прямою х=2 параболою у=1-х² і віссю Ох параболою у=х² і прямою у=х+1 графіком функції у= -х²+4 і прямою х+у=4 графіками функцій у= -х²+2х+8, у=х²+2х+2 лініями у=0, у= -х²+3, х=1, х=1,5 кривою у=х³ і прямими у=1, х=-2 параболою у=х²+2х-8 і віссю Ох.

Об'єм тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями Розв'язання. Формула обчислення об'єму тіла, утвореного обертанням криволінійної трапеції навколо осі Ох: Відповідь:

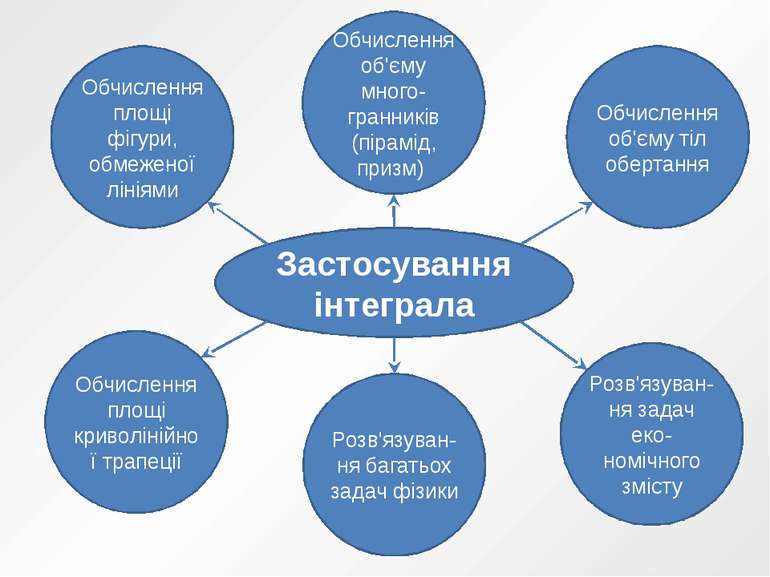
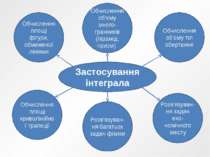
Застосування інтеграла Обчислення площі фігури, обмеженої лініями Обчислення об'єму много-гранників (пірамід, призм) Обчислення об'єму тіл обертання Розв'язуван-ня задач еко-номічного змісту Розв'язуван-ня багатьох задач фізики Обчислення площі криволінійної трапеції

МОЛОДЦІ !