Презентація на тему:
Довірчий інтервал для математичного сподівання

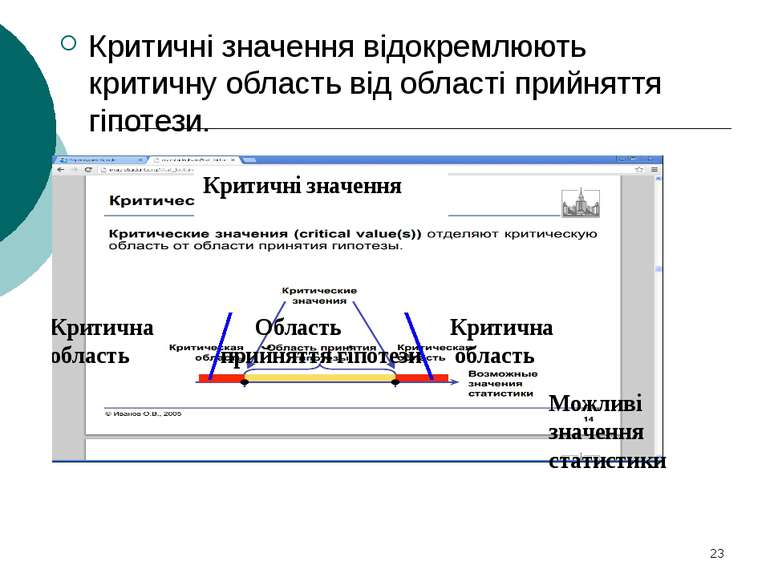
Довірчим називають інтервал (Q* - δ ; Q* + δ ) , що покриває невідомий параметр Q із заданою надійністю γ. P(Q* - δ < Q < Q* + δ ) = γ.

Довірчий інтервал для математичного сподівання що покриває невідомий параметр m з надійністю γ.

Також не важко побачити, що величина вибіркового інтервалу залежить від об’єму вибірки (зменшується із зростанням n) та від значення довірчої ймовірності γ (збільшується при наближенні її до 1).

Довірчий інтервал для середнього квадратичного відхилення (нормальний розподіл) Можна показати, що якщо MX=m невідоме, то довірчий інтервал для середнього квадратичного відхилення має вигляд:

Таблиця для випадкової величини 2 звичайно задається розв’язком рівняння За таблицею для заданої величини q і за числом ступенів вільності n-1 визначаємо q2 (функція EXCEL ХИ2ОБР(q; n-1)).

Приклад. За даними 20 вимірювань знайдене виправлене середньоквадратичне відхилення S=0,12. Знайти точність вимірів з надійністю 0,98.

Точність вимірів характеризується середнім квадратичним відхиленням σ випадкових помилок. Тому задача зводиться до знаходження довірчого інтервалу, що покриває σ із заданою надійністю (0,98).

Використовуючи функцію ХИ2ОБР(q, n-1), знайдемо 12 і 22 . Для ступенів вільності n - 1=19 і ймовірності α2=(1-0,98)/2=0,01 знаходимо 22 =36,2, а потім для n - 1=19 і ймовірності α1=(1+0,98)/2=0,99 знаходимо 12 =7,63. 22 =ХИ20БР(0,01; 19)=36,2 ; 12 =ХИ20БР(0,99;19)=7,63.

Знаходимо Шуканий довірчий інтервал (0,09;0,19).

СТАТИСТИЧНА ПЕРЕВІРКА СТАТИСТИЧНИХ ГІПОТЕЗ

Методи математичної статистики дозволяють перевірити: припущення про закон розподілу деяких випадкових величин (генеральної сукупності); про значення параметрів цього розподілу; про наявність кореляційної залежності між випадковими величинами, визначених на множині об'єктів однієї і тієї ж генеральної сукупності.

Статистичною називають гіпотезу про вигляд невідомого розподілу, про параметри відомих розподілів. Задача полягає в тому, щоб підтвердити або спростувати гіпотезу, використовуючи вибіркові (експериментальні) дані.

Перевірити статистичну гіпотезу – це означає перевірити, чи узгоджуються вибіркові дані з цією гіпотезою. Перевірка здійснюється за допомогою статистичного критерію.

Статистичний критерій – це випадкова величина, закон розподілу якої (разом із значеннями параметрів) відомий у випадку, якщо прийнята гіпотеза справедлива. Звичайно використовуються критерії Стьюдента, Фішера, χ2 (Пірсона) та ін.

Послідовність дій Крок 1. Сформулювати основну та альтернативну гіпотези. Крок 2. Задати рівень значущості α. Крок 3. Обираємо критерій для перевірки гіпотези Крок 4. По таблиці знайти критичні значення та побудувати критичну область. Крок 5. За вибіркою порахувати значення статистики. Крок 6. Порівняти отримане значення з критичною областю. Зробити висновок

1. Сформулювати основну та альтернативну гіпотези. Нульовою (основною) гіпотезою називають висунуту гіпотезу Н0. Разом з нульовою гіпотезою Н0 висувається альтернативна або конкуруюча гіпотеза Н1 , що суперечить нульовій. Наприклад : 1)Н0 : Q1 = Q2; 2) Н0 : Q1 = Q2; 3) Н0 : Q1 = Q2; Н1 : Q1 > Q2 ; Н1 : Q1 < Q2; Н1 : Q1 ≠Q2.

2. Задати рівень значущості α. Виберемо деяку малу величину α (0,05; 0,01; 0,001) – рівень значущості . Ймовірність α називають рівнем значущості. Це ймовірність здійснення помилки першого роду, тобто відкидання гіпотези Н0, коли вона вірна.

3. Обираємо критерій для перевірки гіпотези Нехай випадкова величина К – статистичний критерій перевірки деякої гіпотези Н0. При справедливості Н0 закон розподілу випадкової величини К характеризується деякою відомою щільністю розподілу ймовірності p(K).

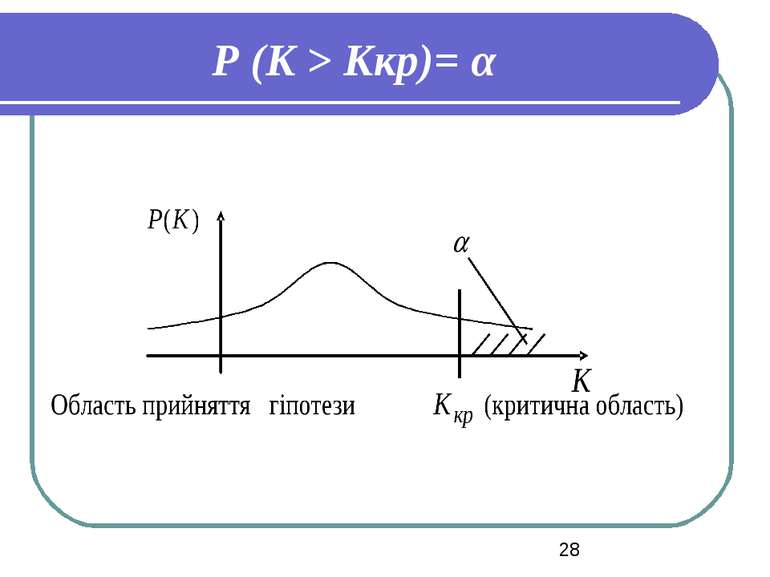
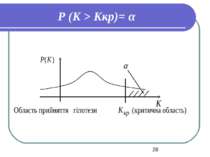
4. Знайти критичні значення та побудувати критичну область. Визначимо критичне значення критерію Ккр як розв’язок одного з трьох рівнянь залежно від вигляду Н0 та Н1 . 1) Н0 : Q1 = Q2; Н1 : Q1 > Q2 Р (K > Kкритичне)= α , (1)

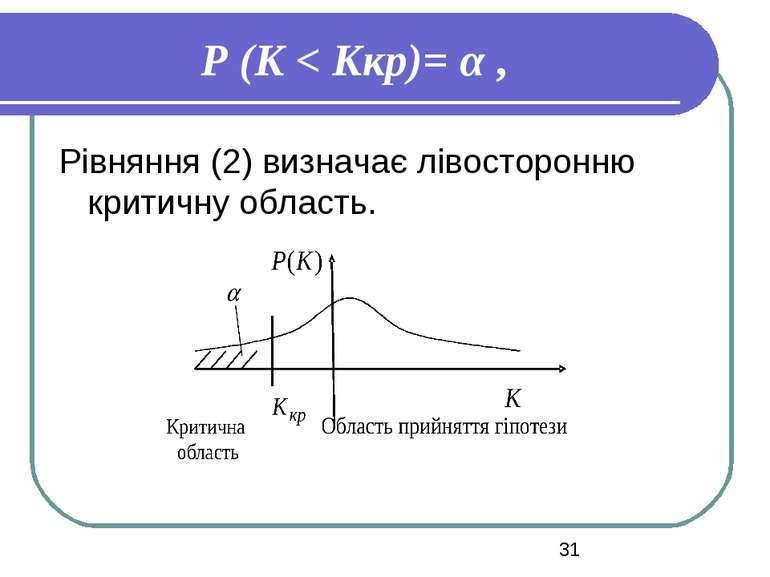
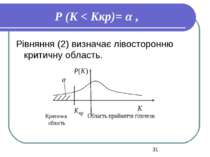
2) Н0 : Q1 = Q2; Н1 : Q1 < Q2 Р (K < Kкритичне)= α , (2) 3) Н0 : Q1 = Q2; Н1 : Q1 ≠ Q2 Р (K < Kкритичне1) + Р (K > Kкритичне2)= α. (3)

Розв’язок рівнянь (1–3) полягає в такому: за заданою імовірністю α, знаючи p(K), задану, як правило, у вигляді таблиць, потрібно визначити критичне значення критерію (Kкритичне).

Критичні значення відокремлюють критичну область від області прийняття гіпотези.

Множина значень статистики включає дві області: 1 Область прийняття гіпотези, тобто безліч тих значень статистики, при яких гіпотеза Н0 приймається; 2 Критичну область, тобто безліч тих значень статистики, при яких гіпотеза Н0 відхиляється і приймається альтернативна гіпотеза Н1.

5. За вибіркою порахувати значення статистики. Після побудови критичної області обчислюють значення статистики по вибірці і порівнюють його з критичною областю.

6. Порівняти отримане значення з критичною областю. Зробити висновок Якщо значення статистики потрапило в область прийняття гіпотези, то гіпотеза Н0 приймається Якщо значення статистики потрапило в критичну область, то гіпотеза H0 відхиляється і приймається альтернативна гіпотеза H1

Розглянемо рівняння Р (K > Kкритичне)= α (1). Розв’язавши його, знаходимо значення Kкритичне, що розбиває числову вісь на дві області: K< Kкритичне– область прийняття гіпотези; K> Kкритичне– критична область.

Р (K > Kкр)= α

Критична точка, що отримана з рівняння (1), називається правобічною. Обчислюємо Kемпіричне – значення критерію K, розраховане за вибірковими даними

Правило: якщо Кемпіричне > Ккритичне – У цьому випадку говорять, що гіпотеза H0 не узгоджується з вибірковими даними. H0 відкидається; Кемпіричне < Ккритичне– вибіркові дані не суперечать гіпотезі H0. H0 приймається.

Р (K < Kкр)= α , Рівняння (2) визначає лівосторонню критичну область.

Правило: якщо Кемпіричне < Ккритичне– H0 відкидається; Кемпіричне> Ккритичне– H0 приймається.

Рівняння (3) визначає двосторонню критичну область. Звичайно Кkр1 і Кkр2 визначають таким чином, щоб виконувалася умова .

Правило: |Kемпіричне|>Kкритичне – H0 відкидається , |Kемпіричне|

Перевірка гіпотези про закон розподілу Нехай необхідно перевірити гіпотезу Н0 про те, що вибірка підкоряється певному закону розподілу, заданому функцією F0(x). Під альтернативною гіпотезою H1 в цьому випадку будемо підрозумівати те, що просто не виконано основну гіпотезу. Потрібно зробити висновок: чи погоджуються результати спостережень із висловленим припущенням. Для цього використаємо спеціально підібрану величину – критерій згоди.

Критерій згоди Пірсона – найбільш часто вживаний критерій для перевірки гіпотези про закон розподілу. Для перевірки гіпотези про закон розподілу необхідно розрахувати емпіричні і теоретичні частоти.

Емпіричні та теоретичні частоти. Безперервний розподіл Нехай при дослідженні випадкової величини була отримана вибірка розміром n. Весь інтервал можливих значень поділяють на k інтервалів. Інтервали не перетинаються і рівні між собою. Потім обчислюють ni– кількість значень, що потрапили в i-й інтервал. Емпіричними називають частоти ni, що фактично спостерігаються .

Теоретичні частоти безперервного розподілу знаходять за формулою , де N – число випробувань; Pi– ймовірність влучення X у i-й частковий інтервал, обчислена при допущенні, що X має функцію розподілу F(x).

Зокрема, якщо є підстави припускати, що випадкова величина X розподілена нормально, то теоретичні частоти, обчислюють таким чином

де N – число випробувань; xi – права границя i-го інтервалу; – середнє значення; S – стандартне відхилення.

Критерій згоди Пірсона Нульова гіпотеза: генеральна сукупність розподілена за законом F(x). В якості критерію обираємо випадкову величину де ni – емпіричні частоти; ni’ – теоретичні частоти.

Для рівня значущості α знаходимо 2kp , розв’язуючи рівняння P( 2> 2критичне )= α, 2критичне=Хи2Обр(α,K), де K = L - 1 - r ; L – число часткових інтервалів; r – число параметрів розподілу. Для нормального закону r = 2.

Якщо 2 емпіричне< 2критичне – гіпотезу про закон розподілу приймаємо. Якщо 2 емпіричне > 2критичне – гіпотезу Н0 відкидаємо. Обсяг вибірки повинен бути більше ніж 50.

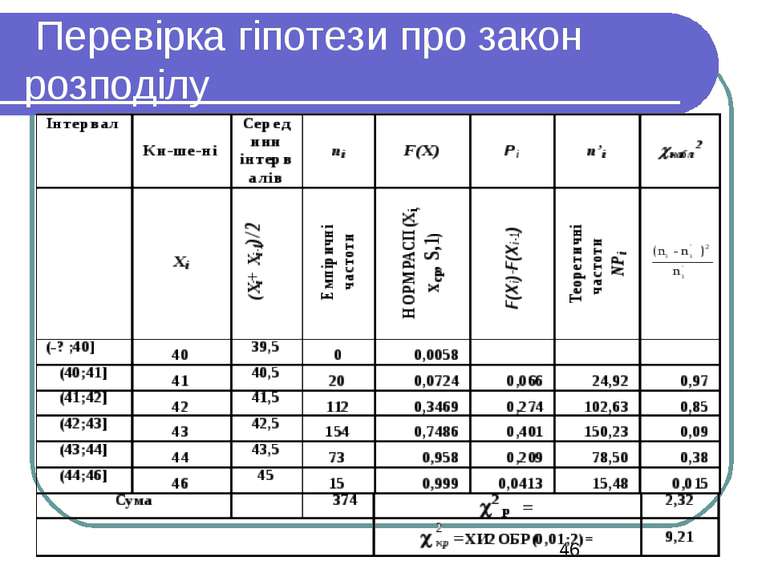
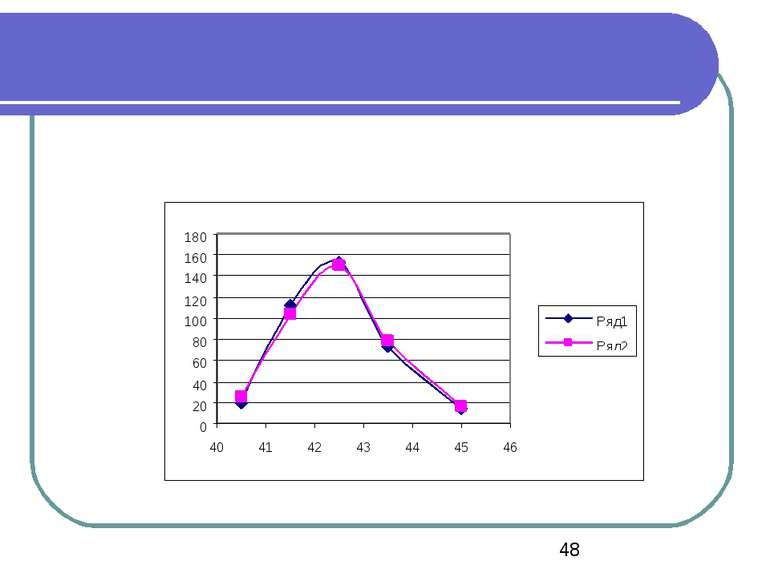
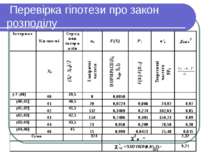
Приклад У таблиці наведені значення частот. Розрахувати теоретичні частоти в припущенні, що вибірка має нормальний закон розподілу. Відомо, що =42,37, S=0,94. З рівнем значущості α=0,01 перевірити гіпотезу про закон розподілу.

Оскільки =42,37, S=0,94, нормальний закон розподілу для нашої вибірки можна записати у вигляді N(42,37; 0,94).

Перевірка гіпотези про закон розподілу

Для розглянутого прикладу 2 = 2,32. 2 критичне= Хи2Обр(0,01; 2) = 9,210351 (K = 5 – 1 – 2 = 2). Оскільки 2 р< 2 критичне, гіпотеза про нормальний закон розподілу N(20,27; 1,96) приймається з рівнем значущості 0,01.