Презентація на тему:
Інтервали

Тема 4 Квадратні нерівності та системи рівнянь другого степеня Розв’язування нерівностей другого степеня з однією змінною. Графічний спосіб. Розв’язування нерівностей другого степеня з однією змінною. Аналітичний спосіб Метод інтервалів Степінь рівняння з двома змінними. Розв’язування систем рівнянь з двома змінними Розв’язування вправ. Самостійна робота Розв’язування текстових задач складанням систем рівнянь з двома змінними

Пункт 5.3. Коли квадратний тричлен має два корені, то нерівність чи можна розв'язати способом, який називається методом інтервалів. Розв’язування нерівностей другого степеня з однією змінною. Метод інтервалів

Запитання для самоперевірки Які квадратні нерівності можна розв'язати методом інтервалів? У чому суть методу інтервалів? Які ще нерівності, крім квадратних, можна розв'язати методом інтервалів?

Пункт 5.3. Розв'язання Розкладемо на множники тричлен, що стоїть у лівій частині нерівності. Оскільки коренями тричлена є: х1=3, х2=4, то х2-7х+12=(х-3)(х-4). Отже, дана нерівність рівносильна нерівності (х-3)(х-4) < 0. Числа 3 і 4 розбивають числову пряму на три проміжки (інтервали): (-∞; 3), (3; 4), (4; ∞). Позначимо їх на координатній прямій (рис.). Визначимо знак добутку на кожному з них. 1). Проміжок (інтервал) (-∞; 3), тобто х < 3. За цієї умови обидва множники набувають від'ємних значень: x – 3 < 0 і x – 4 < 0. Отже, їх добуток є додатним числом: (x - 3) (x - 4) > 0. 2). Інтервал (3; 4), тобто 3 < x < 4. За цієї умови x – 3 < 0 і x – 4 > 0. Отже, (x - 3) (x - 4) < 0. 3). Інтервал (4; ∞), тобто x > 4. За цієї умови x – 3 > 0 і x – 4 > 0. Отже, (x - 3) (x - 4) > 0. Те, як змінюється знак даного добутку показуємо на рисунку. Таким чином, (x - 3) (x - 4) < 0 при 3 < x < 4, тобто на проміжку (3; 4). Суть методу інтервалів Приклад 1. Розв'язати нерівність: Х2-7х+12

Пункт 5.3. Для встановлення загального способу розв'язання аналогічних нерівностей розглянемо функцію f(x) = х2 - 7х + 12, або f(х)=(х–3)(x-4). Проаналізуємо зміну знака функції на визначених числових проміжках. На інтервалі (-∞; 3), тобто х < 3 функція набуває додатних значень. При переході через точку х=3 вона змінює свій знак на протилежний, тобто на інтервалі (3; 4) значення функції від'ємні. При переході через точку х=4 функція знову змінює свій знак - на інтервалі (4; ∞) її значення є додатними. Таким чином, при русі по координатній прямій зліва направо від одного інтервалу до іншого знак функції f(х) = (х – 3)(х - 4) почергово змінюється. Послідовність розв'язання

Пункт 5.3. Нерівність (х – 3)(х - 4) < 0 можна розв'язати так: 1). Знаходимо нулі функції f(х) = (х – 3)(х – 4): х=3 і х=4. 2). Позначаємо отримані числа на координатній прямій і знаходимо відповідні інтервали. 3). Визначаємо знак функції, наприклад, на крайньому зліва інтервалі. Для цього можна взяти будь-яке значення х з цього інтервалу і, підставивши його у формулу, що задає функцію, знайти знак кожного множника, а потім і добутку. 4). Визначаємо знак функції на наступних інтервалах, розставивши їх у порядку чергування. 5). З усіх інтервалів вибираємо ті, на яких значення функції мають вказаний в умові знак. Алгоритм розв'язання

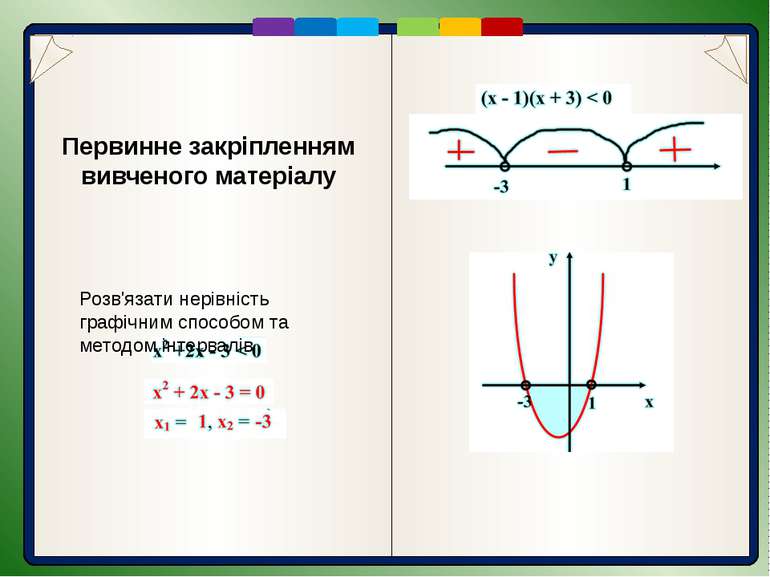
Первинне закріпленням вивченого матеріалу Розв'язати нерівність графічним способом та методом інтервалів

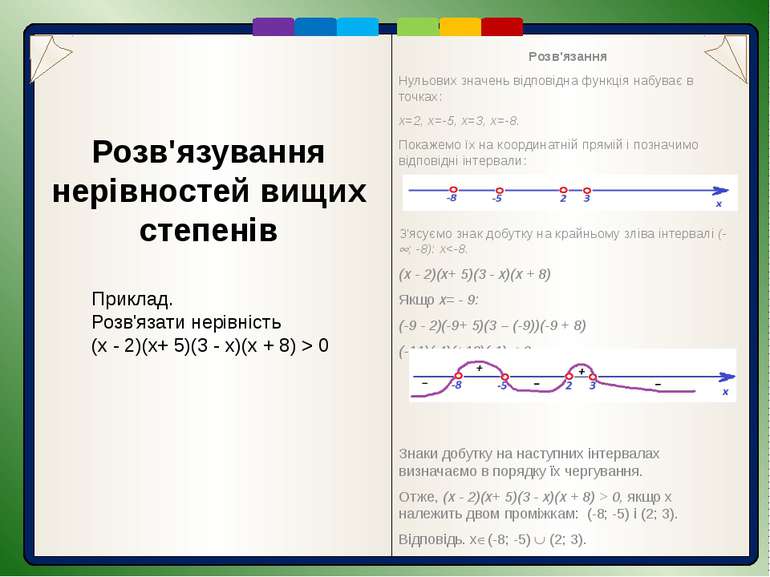
Розв'язання Нульових значень відповідна функція набуває в точках: х=2, х=-5, х=3, х=-8. Покажемо їх на координатній прямій і позначимо відповідні інтервали: З'ясуємо знак добутку на крайньому зліва інтервалі (- ; -8): х 0, якщо х належить двом проміжкам: (-8; -5) і (2; 3). Відповідь. х (-8; -5) (2; 3). Розв'язування нерівностей вищих степенів Приклад. Розв'язати нерівність (x - 2)(x+ 5)(3 - x)(x + 8) > 0

Первинне

Розв'язання Розв'язання Нульових значень відповідна функція набуває в точках: х=2, х=-5, х=3, х=-8. Покажемо їх на координатній прямій і позначимо відповідні інтервали: З'ясуємо знак добутку на крайньому зліва інтервалі (- ; -8): х&lt;-8. (x - 2)(x+ 5)(3 - x)(x + 8) Якщо х= - 9: (-9 - 2)(-9+ 5)(3 – (-9))(-9 + 8) (-11)(-4)(+12)(-1) &lt; 0 Знаки добутку на наступних інтервалах визначаємо в порядку їх чергування. Отже, (x - 2)(x+ 5)(3 - x)(x + 8) &gt; 0, якщо х належить двом проміжкам: (-8; -5) і (2; 3). Відповідь. х (-8; -5) (2; 3).

Запитання