Презентація на тему:
Науковці математичного аналізу

Творці математичного аналізу

Наука, що на сьогодні називається математичним аналізом, виникла в працях багатьох видатних математиків XVII століття - спочатку у вигляді окремих теорем та методів розв'язування деяких задач. До кінця XVII століття основні положення цієї нової для того часу науки остаточно оформилися (причому одночасно) в роботах двох найвизначніших учених тієї епохи - англійського фізика та математика Ньютона та німецького математика і філософа Лейбніца.

Левіш

Ньютон

Виникнення цієї математичної дисципліни не випадково припадає саме на XVII століття. У цю епоху розвиток науки та техніки дійшов тієї межі, коли для подальшого просування вперед необхідно було глибше проникнути у суть речей, вивчити закони природи та процеси, що відбуваються в навколишньому середовищі. Всі процеси протікають з певною швидкістю, всі величини, що беруть участь у цих процесах, змінюються, причому вони взаємозв'язані. Тому постала необхідність у такому апараті, за допомогою якого можна було б вивчати змінні процеси. Саме такий апарат і був розроблений у математичному аналізі. Таким чином, виникнення математичного аналізу було історично неминучим: цього вимагали потреби механіки, фізики та техніки. У свою чергу, саме ці вимоги були визначені рівнем розвитку виробничих сил суспільства. Проте повне його обґрунтування було дано лише наприкінці XIX століття. Ключовими поняттями математичного аналізу є поняття функції, границі, похідної та інтеграла.

Термін „функція" вперше запропонував у 1692 р. видатний німецький філософ і математик Готфрід Вільгельм Лейбніц (1646-1716) для характеристики відношення відрізків, а перше означення функції, яке вже не було пов'язане з геометричними уявленнями, сформулював Йоган Бернуллі (1667-1748) у 1718 р.

Уточнив це поняття Леонард Ейлер (1707-1783) і ввів символ функції f(x).

Термін „границя" і відповідний символ lim вперше було введено англійським математиком і механіком Ісааком Ньютоном (1643-1727), а його строге означення сформулював у 1823 р. французький математик Огюстен Луї Коші (1789-1857).

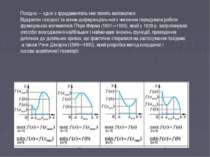
Похідна — одне з фундаменталь них понять математики. Відкриттю похідної та основ диференціаль ного числення передували роботи французьких математиків П'єра Ферма (1601—1665), який у 1629 р. запропонував способи знаходження найбільших і найменших значень функцій, проведення дотичних до довільних кривих, що фактично спиралися на застосування похідних, а також Рене Декарта (1596—1650), який розробив метод координат і основи аналітичної геометрії.

Ферма

Декарт

У 1670—1671 рр. англійський математик і механік Ісаак Ньютон (1643—1727) і дещо пізніше у 1673—1675 рр. німецький філософ і математик Готфрід Вільгельм Лейбніц (1646—1716) незалежно один від одного побудували теорію диференціального числення. І.Ньютон прийшов до поняття похідної, розв'язуючи задачі про миттєву швидкість, а Лейбніц — розглядаючи геометричну задачу про проведення дотичної до кривої. Термін «похідна» ввів у 1797 р. французький математик Жозеф Луї Лагранж (1736—1813). Він ввів і сучасні позначення для похідної у вигляді та f./. Сам термін «похідна» є перекладом відповідного французького слова derivee, яке досить влучно пояснює зміст цього поняття: функція f'(x) у певному розумінні походить від функції f(x), тобто є похідною від неї.

Лагранж

До Лагранжа похідну за пропозицією Лейбніца називали диференціальним коефіцієнтом і позначали dy/dx . Позначення Лейбніца чітко відображало саме походження похідної як границі відношення dy/dx. Тому його часто використовують і в сучасних курсах математичного аналізу. Ньютон, який у своїх підходах до обґрунтування математичного аналізу широко застосовував фізичні уявлення, похідну називав флюксією (дослівно з латини — «витіканням»), а саму функцію флюентною (дослівно «текучістю»). Ці терміни Ньютона не прижилися. Терміни «диференціальний», «диференційована», «диференціювання» тощо відображають той аспект утворення поняття похідної, що пов'язаний із знаходженням різниць f(x)-f(x0) = y та х—х0 = x (differentia в перекладі з латини означає «різниця»).

Велику роль у розвитку диференціального числення відіграв видатний математик, фізик, механік і астроном Леонард Ейлер, який написав підручник «Диференціальне числення» (1755 р.) За допомогою диференціального числення було розв'язано багато задач теоретичної механіки, фізики та астрономії. Зокрема, використовуючи методи диференціального числення, вчені передбачили повернення комети Галлея, що стало тріумфом науки XVIII ст. За допомогою цих методів математики у XVIII ст. вивчали властивості різних кривих, знайшли криву, по якій найшвидше падає матеріальна точка, навчилися знаходити кривину ліній. І тепер поняття похідної широко застосовується у різних галузях науки та техніки.