Презентація на тему:
Поняття математичного моделювання

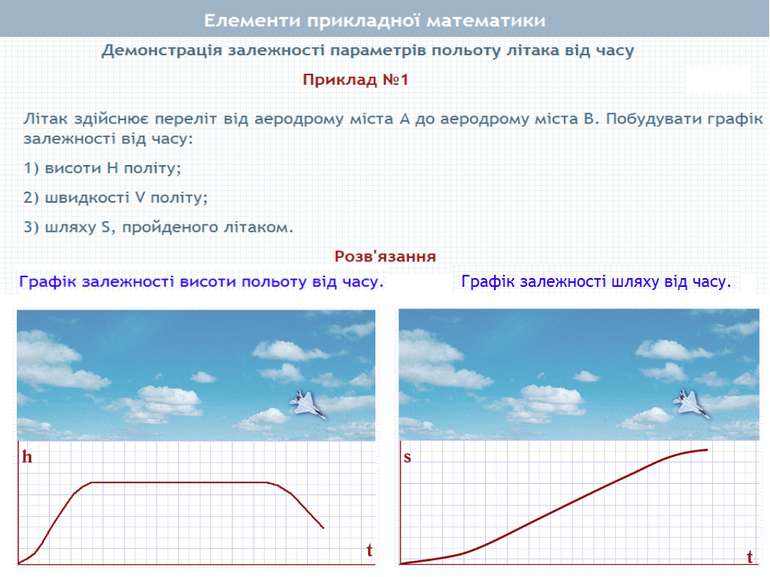
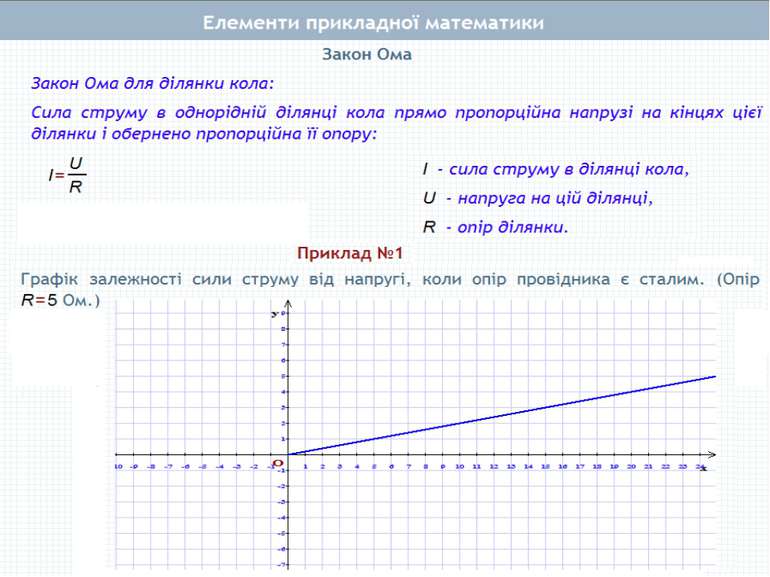
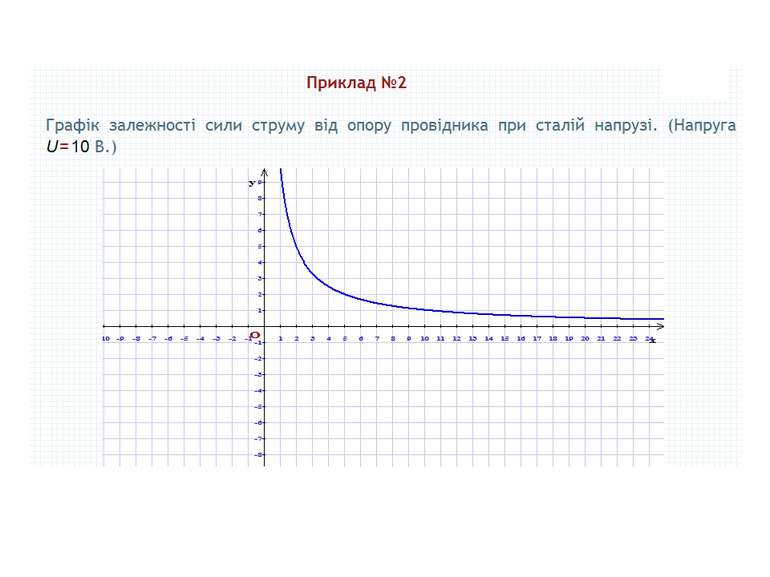
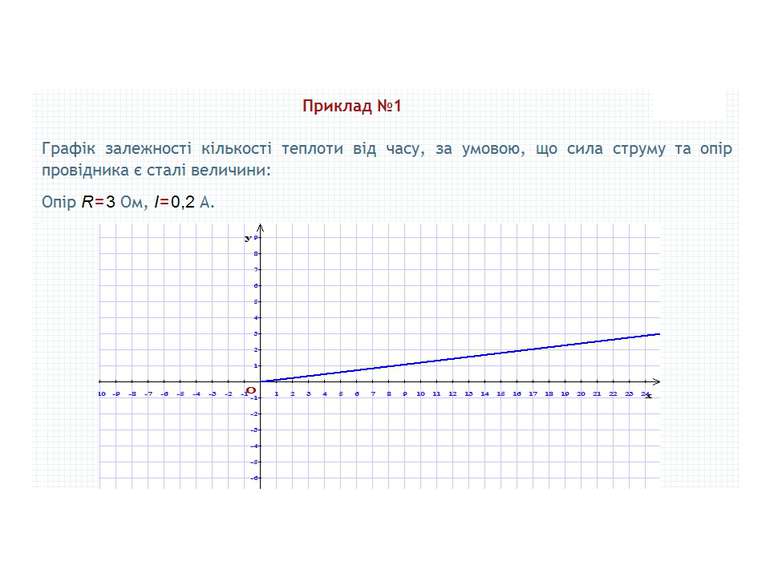
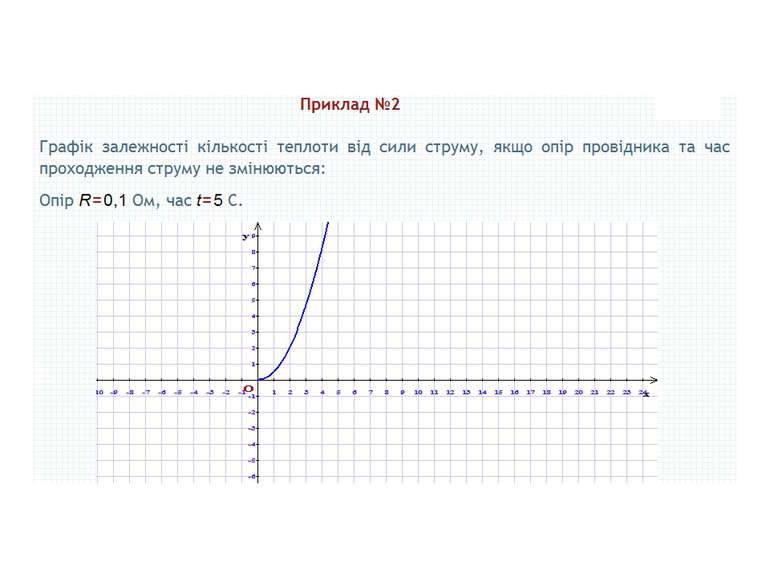
Тема 5 Елементи прикладної математики Математичне моделювання Відсоткові розрахунки. Поняття про теорію імовірностей. Основні поняття теорії імовірностей. Ймовірність випадкової події Початкові відомості про математичну статистику. Статистичні дані. Способи подання даних Середнє значення. Розв'язування вправ

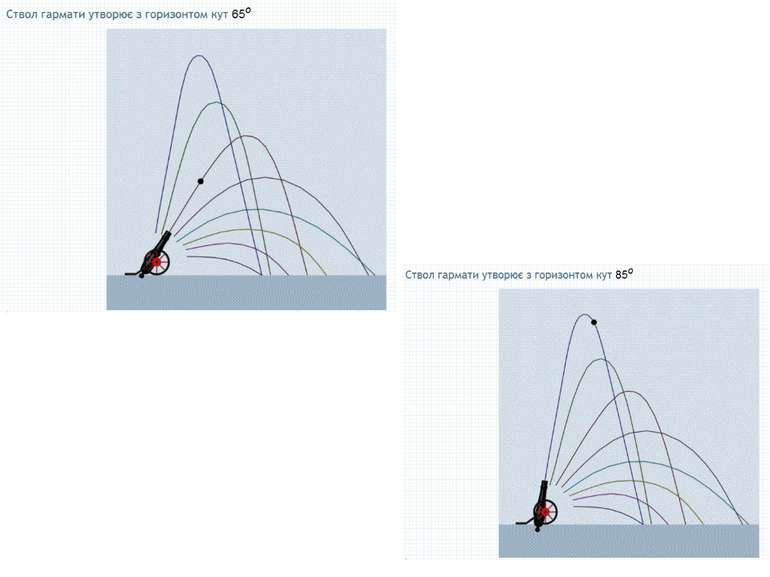
Пункт 7.1. Упродовж усього часу існування математики як науки значну частину наукових пошуків займали і продовжують займати розв'язання численних прикладних задач. Такі задачі описують певні ситуації, які виникають у житті, в різних сферах людської діяльності. Для того, щоб розв'язати певну прикладну задачу математичними методами її зміст перекладають на мову математики. В результаті отримують математичну модель початкової задачі, де вже фігурують не реальні об'єкти, а абстрактні математичні поняття, числа, вирази, відношення. Математичною моделлю прикладної задачі може бути рівняння, нерівність, функція, система рівнянь або нерівностей. Поняття математичного моделювання

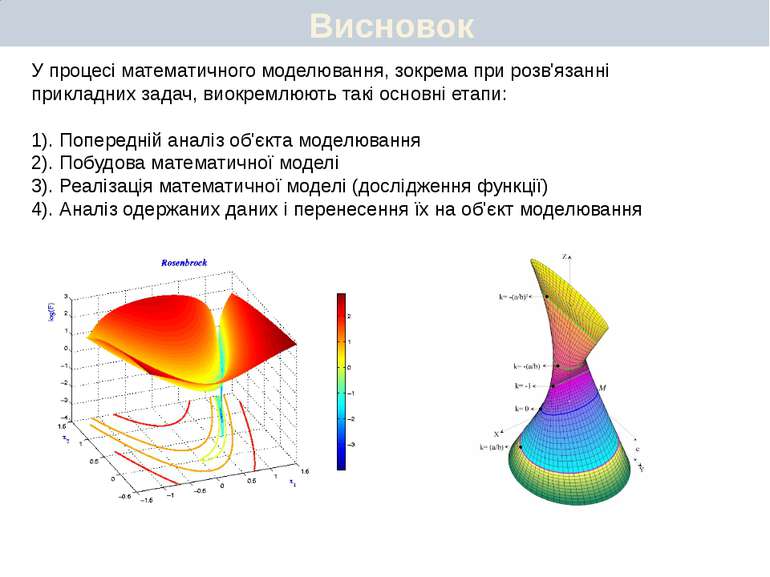
Висновок У процесі математичного моделювання, зокрема при розв'язанні прикладних задач, виокремлюють такі основні етапи: 1). Попередній аналіз об'єкта моделювання 2). Побудова математичної моделі 3). Реалізація математичної моделі (дослідження функції) 4). Аналіз одержаних даних і перенесення їх на об'єкт моделювання

Пункт 7.1. Розглянемо прикладну задачу, математичною моделлю якої є функція, і прослідкуємо процес створення та реалізації цієї моделі. Задача. Дитячий майданчик прямокутної форми, який прилягає до стіни будинку, треба обнести огорожею завдовжки 40 м. Які розміри при цьому повинен мати майданчик, щоб його площа була найбільшою? Розв'язання. Проаналізуємо умову і зробимо відповідний рисунок. Майданчик зображено на ньому у формі прямокутника ABCD, одна сторона AD якого прилягає до стіни. Отже, огорожа майданчика проляже вздовж сторін АВ, ВС і CD. Позначимо довжину однієї з них, наприклад АВ, через х. Тоді довжина сторони ВС становитиме 40 - 2х. Процес математичного моделювання

Пункт 7.1. За умовою задачі площа прямокутника ABCD має бути найбільшою. За відомою формулою, SABCD= АВ ВС = х(40 - 2х). Залишається знайти, при яких значеннях х значення цього добутку буде найбільшим. Отже, розв'язання даної прикладної задачі звелося до розв'язання винятково математичної задачі: при яких значеннях змінної х вираз х(40 - 2х) або функція у = х(40 - 2х) набуває найбільшого значення. Ця функція і є математичною моделлю даної прикладної задачі. Функція у = х(40 - 2х) або у=-2х2+40х є квадратичною функцією. Коефіцієнт при х2 - від'ємне число, тобто функція набуває найбільшого значення у вершині параболи, в точці х=-b/2a=40 4=10. Процес математичного моделювання

Первинне закріплення вивченого матеріалу

Запитання для самоперевірки 1). Для чого створюють математичні моделі? 2). Наведіть приклади математичних моделей реальних процесів, прикладних задач. 3). Які основні етапи можна виокремити у процесі математичного моделювання?