Презентація на тему:
числові функції

Числові функції

Епіграф Те, що я чую, я забуваю. Те, що я бачу й чую, я трошки пам’ятаю. Те, що я чую, бачу, обговорюю, я починаю розуміти. Коли я чую, бачу, обговорюю й роблю, я набуваю знань і навичок. Конфуцій.

Домашнє завдання 1

Домашнє завдання 2

Домашнє завдання 3

Графік функції

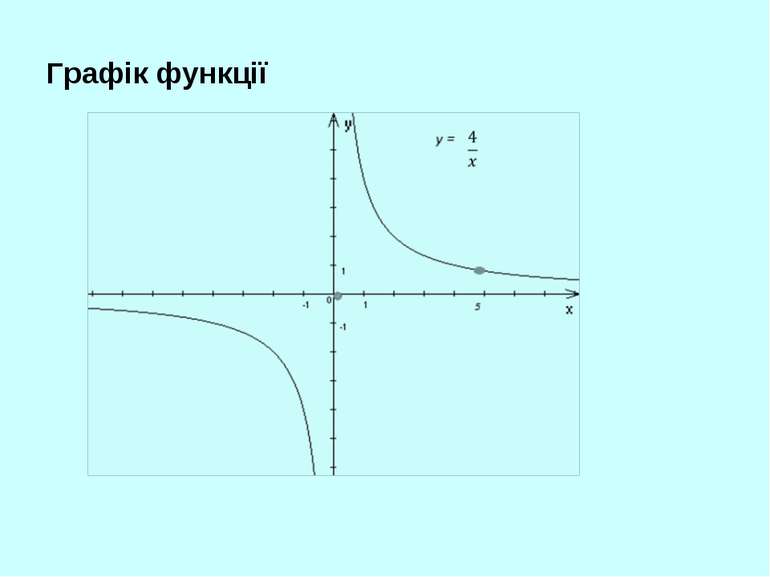
2. Математична розминка Які змінні називаються функціонально залежними? Відповідь. Кожному значенню незалежної змінної відповідає одне і тільки одне значення залежної змінної. 2. Сформулювати означення числової функції. Відповідь. Нехай D – деяка множина дійсних чисел. Числовою функцією з областю визначення D називають таку залежність, при якій кожному числу х з множини D відповідає дійсне число y, і записують y = f(x). 3. Способи задання функції. Відповідь. Аналітичний (за формулою) Табличний Графічний.

Математична розминка

Математична розминка

Математична розминка

3. Історична довідка Поняття функції є одним з найважливіших понять математики. Ідея функціональної залежності сягає в глибоку давнину, коли люди тільки почали розуміти існування різних видів залежності в природі. Як і інші, поняття функції виникли з потреб практики. У XVII – XVIII ст. з розвитком мореплавства, судно, машинобудування, астрономії, механіки та інших технічних дисциплін постала необхідність створення математичного апарату для опису різних процесів та явищ. Це привело до появи змінних величин. Значну роль у розвитку цих понять відіграв метод координат французьких математиків П. Ферма (1601-1665) і Р. Декарта (1596 – 1650). Метод координат почали використовувати для графічного дослідження функцій і графічного розв’язування рівнянь. Термін «функція» запровадив німецький математик Г. Лейбніц (1646 – 1716), який функцію пов’язував з графіком.

Вчені древності Р. Декарт (1596 -1650), Французький математик П. Ферма(1601 - 1665), Французький математик Г. Лейбніц (1646 –1716) , німецький математик

Історична довідка (прод.) Академік Петербурської Академії наук Л. Ейлер (1707 – 1783) і швейцарський математик Й. Бернуллі (1667- 1748) вважали функцію аналітичним виразом (формулою). Згодом Л. Ейлер увів загальніший підхід до поняття функції як залежності однієї змінної величини від іншої. Цю ідею розвинули російський математик М. І. Лобачевський (1792 – 1856), німецький математик П. Діріхле (1805 – 1859) та інші вчені.

Л.Ейлер (1707 – 1783), академік Петербурської Академії наук, Й. Бернуллі (1667- 1748), швейцарський математик

П. Діріхле (1805 -1859), німецький математик М.І. Лобачевський (1792 -1856), російський математик

Письмово

Письмово

Письмово

Письмово

Поміркуй

5. Самостійна робота

Відповіді

Відповіді

Підсумок уроку На уроці ми повторили і систематизували знання учнів з теми «Числові функції та їх властивості». Ми переконалися, що ця тема дуже важлива. Адже для вивчення того чи іншого явища потрібно встановлювати взаємозв’язок між величинами, які його описують. Такий взаємозв’язок у математиці задається за допомогою функцій. Розв’язали ряд задач, де застосовувалися властивості числових функцій. Застосовували набуті знання в стандартних і в нестандартних ситуаціях, робили висновки, будувалм графіки функцій за допомогою геометричних перетворень. Переконалися, що дійсно поняття функції є одним з найважливішим поняттям математики.