Презентація на тему:
Аксіоми планіметрії

Геометрія Аксіоми планіметрії

План: аксіома аксіома аксіома аксіома аксіома аксіома аксіома аксіома аксіома

І аксіома Яка б не була пряма, існують точки, що належить цій прямій, і точки, що не належать цій прямій. Через будь-які дві точки можна провести пряму і тільки одну.

ІІ аксіома З трьох точок на прямій одна і тільки одна лежить між двома іншими.

ІІІ аксіома Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.

ІV аксіома Пряма розбиває площину на дві півплощини.

V аксіома Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює 1800. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

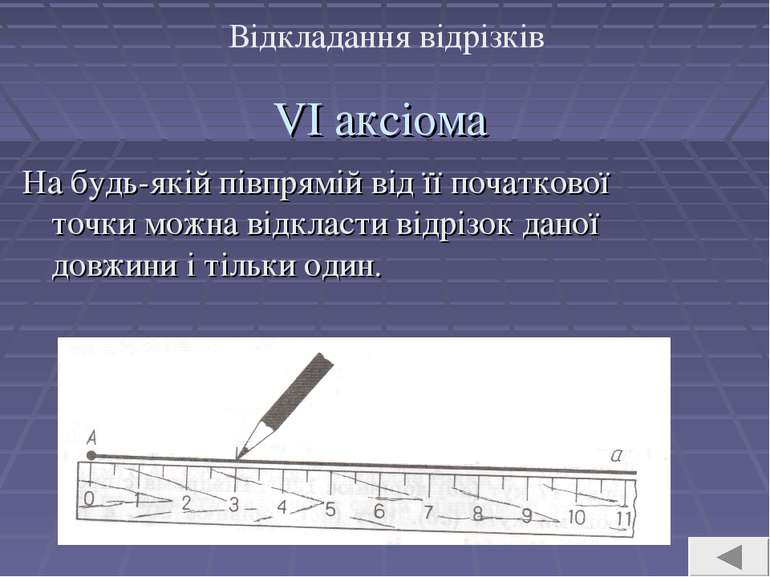
VI аксіома На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини і тільки один.

V II аксіома Від будь-якої півпрямої у дану півплощину можна підкласти кут з даною градусною мірою, меншою за 1800, і тільки один.

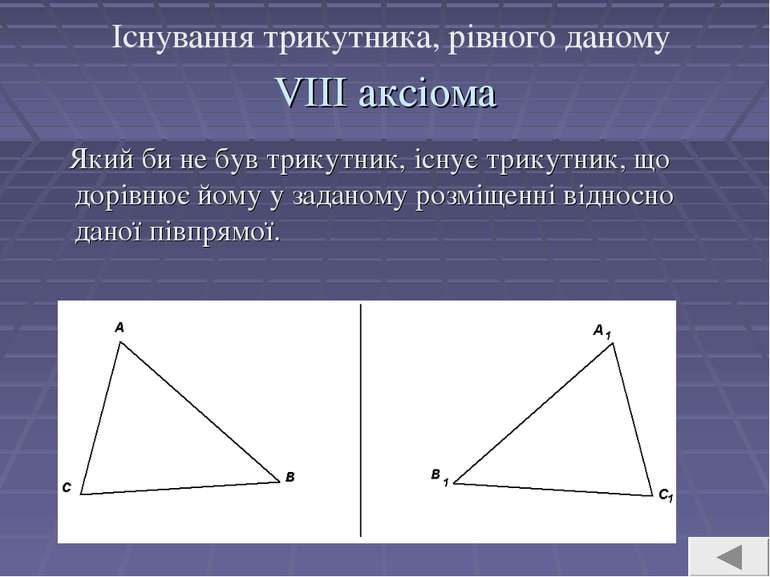
VIII аксіома Який би не був трикутник, існує трикутник, що дорівнює йому у заданому розміщенні відносно даної півпрямої.

ІХ аксіома Через точку, що не лежить на даній прямій, можна провести на площині не більше як одну пряму, паралельну даній.